两参数曲面的相交曲线计算问题

数学星空

对于两个曲面参数方程：

A: \([x_1=f_1(t,k_1),y_1=g_1(t,k_1),z_1=h_1(t,k_1)]\)

B: \([x_2=f_2(t,k_2),y_2=g_2(t,k_2),z_2=h_2(t,k_2)]\)

相交的曲线C如何求解？能否给出其参数表达式？

数学星空

例如：

下面两个参数曲面A和B

[[(-30*k1 + 80)*cos(t), (-30*k1 + 90)*sin(t), 1000 - 1000*k1],

[-h22*(-1 + k2)*sqrt(3)/2 + 5*sin(t)*(-8 + k2), (-10*k2 + 70)*cos(t) + 30 - 30*k2, -5*sin(t)*(-8 + k2)*sqrt(3) - h22*(-1 + k2)/2]]


A和B(h22取常量500)的隐式表达为

(10000*y^2)/(9*(2000 + z)^2) + 10000*x^2/(5000 + 3*z)^2 = 1

2500*(sqrt(3)*x - 3*z)^2/(sqrt(3)*z + 7000*sqrt(3) + 3*x)^2 + (100*sqrt(3)*y - 3*sqrt(3)*z - 9*x)^2/(sqrt(3)*z + 6000*sqrt(3) + 3*x)^2 = 1

参数曲面A和B的图像为：
     
         

        

我们令\(x_1=x_2,y_1=y_2,z_1=z_2\),求得待定参数\(k_1,k_2,h_{22}\)

h22 = (30*cos(t)*(cos(t)^2 - cos(t)*sin(t) - 21*sin(t) - 1)*sqrt(3) - 4000*cos(t)^2 + (-1000*sin(t) - 30000)*cos(t) - 21000*sin(t) - 6000)/((600*cos(t) - 600*sin(t))*sqrt(3) + 24*cos(t)^2 + 3*cos(t)*sin(t) - 42),

k1 = (-10*sin(t)^2 - 2*cos(t)*sin(t) + 100*sqrt(3)*cos(t) - 42*sin(t) - 24*cos(t) + 300*sqrt(3) - 8)/(-3*sin(t)^2 + 100*sqrt(3)*cos(t) + 300*sqrt(3) - 9*cos(t) - 3),

k2 = (-48 + 100*(7*cos(t) - 6*sin(t) + 3)*sqrt(3) + 27*cos(t)^2 + 3*(sin(t) - 3)*cos(t))/(-6 + 100*(3 + cos(t))*sqrt(3) + 3*cos(t)^2 - 9*cos(t))

将所求\(k_1,k_2,h_{22}\)代入原曲面参数方程A,B得到相交曲线C的参数方程：

[5000*((3 + cos(t))*sqrt(3) + (3*sin(t)*(cos(t) + sin(t) + 21))/250)*cos(t)/(-6 + 100*(3 + cos(t))*sqrt(3) + 3*cos(t)^2 - 9*cos(t)),
30*(2*cos(t)*sin(t) - cos(t)^2 + 200*sqrt(3)*cos(t) + 42*sin(t) - 3*cos(t) + 600*sqrt(3))*sin(t)/(-6 + 100*(3 + cos(t))*sqrt(3) + 3*cos(t)^2 - 9*cos(t)),
1000*(12 - 7*cos(t)^2 + (2*sin(t) + 15)*cos(t) + 42*sin(t))/(-6 + 100*(3 + cos(t))*sqrt(3) + 3*cos(t)^2 - 9*cos(t))]

相交曲线图像C为

            

将A,B,C放在同一坐标系得到：

            

明显C的方程有误，请帮忙看看哪里出了问题？？如何求解曲线C的参数方程

Jack315

貌似应该满足 \(k_1=k_2\) 才是两曲面的交线。

mathe

也就是相交曲线满足条件
A: \([x=f_1(t_1,k_1)=f_2(t_2,k_2),y=g_1(t_1,k_1)=g_2(t_2,k_2),z=h_1(t_1,k_1)=h_2(t_2,k_2), ]\)
理论上我们可以消除掉三个参数，只余下一个

Jack315

设两曲面的参数方程分别为：
\(\begin{array}{c}A:\begin{cases}x=f_1(k,t)\\y=g_1(k,t)\\z=h_1(k,t)\end{cases}&B:\begin{cases}x=f_2(k,t)\\y=g_2(k,t)\\z=h_2(k,t)\end{cases}\end{array}\)
联立方程组：
\(\begin{cases}f_1(k_1,t_1)=f_2(k_2,t_2)\\g_1(k_1,t_1)=g_2(k_2,t_2)\\h_1(k_1,t_1)=h_2(k_2,t_2)\end{cases}\)
解得：
\(\begin{cases}k_1=f(t_2)\\k_2=g(t_2)\\t_1=h(t_2)\end{cases}\)
代回到曲面方程（A 或 B）中，并把 t2 换成 t ，即得到曲线的参数方程。
两个曲面共 4 个参变量：\(k_1,t_1,k_2,t_2\) 。三个方程消除 3 个变量，剩下一个是两曲面交线的参变量。

对于所给两个曲面方程的形式，曲线的参数方程没解出来

Jack315

【数值方法】
定义曲面参数方程：

1. fx1[k_, t_] := (-30 k + 80) Cos[t]
   
2. fy1[k_, t_] := (-30 k + 90) Sin[t]
   
3. fz1[k_, t_] := 1000 (1 - k)
   
4. fx2[k_, t_] := Sqrt[3]/2 h (1 - k) - 5 (8 - k) Sin[t]
   
5. fy2[k_, t_] := (70 - 10 k) Cos[t]
   
6. fz2[k_, t_] := 5 Sqrt[3] (8 - k) Sin[t] + h/2 (1 - k)

复制代码

z 值相等，求出 k1:

1. solz = Solve[fz1[k1, t1] == fz2[k2, t2], k1] // Simplify // Flatten
   
2. 【输出】{k1 -> 1 + (h (-1 + k2))/2000 + 1/200 Sqrt[3] (-8 + k2) Sin[t2]}

复制代码

y 值相等，求出 k2:

1. soly = Solve[(fy1[k1, t1] /. solz) == (fy2[k2, t2] /. solz), k2] //Simplify // Flatten
   
2. 【输出】{k2 -> (14000 Cos[t2] - 3 Sin[t1] (4000 + h + 80 Sqrt[3] Sin[t2]))/(2000 Cos[t2] - 3 Sin[t1] (h + 10 Sqrt[3] Sin[t2]))}

复制代码

x 值相等，求出 t1:

1. solx = Solve[(fx1[k1, t1] /. solz /. soly) == (fx2[k2, t2] /. solz /. soly), t1]
   
2. 【输出】……CPU 努力运算中（放弃）。

复制代码

这样可以得到四个计算公式：

1. fx1a = (fx1[k1, t1] /. solz /. soly // Simplify)
   
2. fx2a = (fx2[k2, t2] /. solz /. soly // Simplify)
   
3. fy = fy1[k1, t1] /. solz /. soly // Simplify
   
4. fz = fz1[k1, t1] /. solz /. soly // Simplify

复制代码

给定 h 参数后，就可以逐点计算出交线上点的坐标。参变量为 t2，以 t2 = 0 为例。
求 t1 值（假设 h 取 500）：

1. sol = NSolve[{(fx1a /. {t2 -> 0, h -> 500}) == (fx2a /. {t2 -> 0, h -> 500}), 0 <= t1 <= 2 \[Pi]}, t1, Reals] // Flatten
   
2. 【输出】{t1 -> 1.5708, t1 -> 1.58042}

复制代码

求 x 坐标：

1. Table[fx1a /. {t2 -> 0, h -> 500} /. sol[[i]], {i, Length[sol]}]
   
2. 【输出】{3.06162*10^-15, -0.481021}
   
3. Table[fx2a /. {t2 -> 0, h -> 500} /. sol[[i]], {i, Length[sol]}]
   
4. 【输出】{0., -0.481021}

复制代码

求 y 坐标：

1. Table[fy /. {t2 -> 0, h -> 500} /. sol[[i]], {i, Length[sol]}]
   
2. 【输出】{60., 59.9889}

复制代码

求 z 坐标：

1. Table[fz /. {t2 -> 0, h -> 500} /. sol[[i]], {i, Length[sol]}]
   
2. 【输出】{0., -0.277717}

复制代码

对应 t2 = 0，t1=(1.5708, 1.58042)，交线上两个点的坐标为：(0, 60, 0), (-0.4810, 59.9889, -0.2777) 。

Jack315

【两平面相交直线的参数方程】
平面 A:
\(\begin{cases}fx_1(s,t)=-1+2s-t\\fy_1(s,t)=1+s+t\\fz_1(s,t)=2-s+2t\end{cases}\)

1. fx1[s_, t_] := x01 + s x11 + t x21
   
2. fy1[s_, t_] := y01 + s y11 + t y21
   
3. fz1[s_, t_] := z01 + s z11 + t z21
   
4. pts1 = {x01 -> -1, y01 -> 1, z01 -> 2, x11 -> 2, y11 -> 1, z11 -> -1, x21 -> -1, y21 -> 1, z21 -> 2}

复制代码

平面 B:
\(\begin{cases}fx_2(s,t)=2-2s+t\\fy_2(s,t)=1+s+2t\\fz_2(s,t)=-1+2s-t\end{cases}\)

1. fx2[s_, t_] := x02 + s x12 + t x22
   
2. fy2[s_, t_] := y02 + s y12 + t y22
   
3. fz2[s_, t_] := z02 + s z12 + t z22
   
4. pts2 = {x02 -> 2, y02 -> 1, z02 -> -1, x12 -> -2, y12 -> 1, z12 -> 2, x22 -> 1, y22 -> 2, z22 -> -1}

复制代码

联立方程求解：
\(\begin{array}{cc}
\begin{cases}fx_1(s_1,t_1)=fx_2(s_2,t_2)\\fy_1(s_1,t_1)=fy_2(s_2,t_2)\\fz_1(s_1,t_1)=fz_2(s_2,t_2)\end{cases}
\rightarrow&
\begin{cases}s_1=1+\frac{5}{3}t_2\\s_2->-2t_2\\t_1=-1-\frac{5}{3}t_2\end{cases}
\end{array}\)

1. sol = Solve[{fx1[s1, t1] == fx2[s2, t2], fy1[s1, t1] == fy2[s2, t2], fz1[s1, t1] == fz2[s2, t2]}, {s1, s2, t1}] /. pts1 /. pts2

复制代码

代入平面 A 中得直线的参数方程：
\(\begin{cases}fx(t)=2+5t\\fy(t)=1\\fz(t)=-1-5t\end{cases}\)

1. fx1[s1, t1] /. sol /. pts1 /. pts2 // Simplify
   
2. fy1[s1, t1] /. sol /. pts1 /. pts2 // Simplify
   
3. fz1[s1, t1] /. sol /. pts1 /. pts2 // Simplify

复制代码

可视化验证：

1. 
   
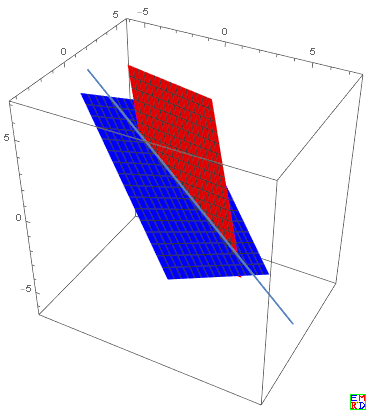
2. Show[{
   
3. ParametricPlot3D[{fx1[s, t], fy1[s, t], fz1[s, t]} /. pts1,{s, -0.5, 1.5}, {t, -2, 2}, PlotStyle -> Red],
   
4. ParametricPlot3D[{fx2[s, t], fy2[s, t], fz2[s, t]} /. pts2,{s, -1, 2.5}, {t, -2, 1}, PlotStyle -> Blue],
   
5. ParametricPlot3D[{fx1[s1, t1], fy1[s1, t1], fz1[s1, t1]} /. sol /. pts1 /. pts2, {t2, -1.5, 1}]
   
6. }]
   

复制代码

Jack315

【接 6 #】
4 个计算公式为：
\(\begin{cases}
f_{x1a}(t_1,t_2,h)=\frac{10\cos⁡{t_1}[3\sin{t_1}(h+10\sqrt{3}\sin{t_2})+2\cos{t_2}(5000-9h+15\sqrt{3}\sin{t_2})]}{2000\cos{t_2}-3\sin{t_1}(h+10\sqrt{3}\sin{t_2})}\\
f_{x2a}(t_1,t_2,h)=\frac{-2000\cos{t_2}(3\sqrt{3}h+5\sin{t_2})+60\sin{t_1}[100\sqrt{3}h+(-1000+7h)\sin{t_2}]}{2000\cos{t_2}-3\sin{t_1}(h+10\sqrt{3}\sin{t_2})}\\
f_y(t_1,t_2,h)=\frac{60\cos{t_2}\sin{t_1}(2000-3h+5\sqrt{3}\sin{t_2})}{2000\cos{t_2}-3\sin{t_1}(h+10\sqrt{3}\sin{t_2})}\\
f_z(t_1,t_2,h)=-\frac{2000[\cos{t_2}(3h-5\sqrt{3}\sin{t_2})-3\sin{t_1}(h+10\sqrt{3}\sin[t_2])]}{2000\cos{t_2}-3\sin{t_1}(h+10\sqrt{3}\sin{t_2})}\\
\end{cases}\)
数值计算函数：

1. getPoints[t20_, h0_] := Module[
   
2.   {fxa, fxb, fy, fz, sol, n, x, y, z, pts},
   
3.   (*参数方程定义*)
   
4.   fxa[t1_, t2_, h_] := (10 Cos[t1] (3 Sin[t1] (h + 10 Sqrt[3] Sin[t2]) + 2 Cos[t2] (5000 - 9 h + 15 Sqrt[3] Sin[t2])))/(2000 Cos[t2] - 3 Sin[t1] (h + 10 Sqrt[3] Sin[t2]));
   
5.   fxb[t1_, t2_, h_] := (-2000 Cos[t2] (3 Sqrt[3] h + 5 Sin[t2]) + 60 Sin[t1] (100 Sqrt[3] h + (-1000 + 7 h) Sin[t2]))/(2000 Cos[t2] - 3 Sin[t1] (h + 10 Sqrt[3] Sin[t2]));
   
6.   fy[t1_, t2_, h_] := (60 Cos[t2] Sin[t1] (2000 - 3 h + 5 Sqrt[3] Sin[t2]))/(2000 Cos[t2] - 3 Sin[t1] (h + 10 Sqrt[3] Sin[t2]));
   
7.   fz[t1_, t2_, h_] := -((2000 (Cos[t2] (3 h - 5 Sqrt[3] Sin[t2]) - 3 Sin[t1] (h + 10 Sqrt[3] Sin[t2])))/(2000 Cos[t2] - 3 Sin[t1] (h + 10 Sqrt[3] Sin[t2])));
   
8.   (*给定参数 t20 和 h0，求解参数 t1 。*)
   
9.   sol = Solve[{fxa[t1, t20, h0] == fxb[t1, t20, h0], 0 <= t1 <= 2 \[Pi]}, t1, Reals] // Flatten;
   
10.   (*计算曲面交线上点的坐标。*)
    
11.   n = Length[sol];
    
12.   If[n > 0,
    
13.    x = List[]; y = List[]; z = List[];
    
14.    For[i = 1, i <= n, i++,
    
15.     AppendTo[x, 1/2 (fxa[t1, t20, h0] + fxb[t1, t20, h0]) /. sol[[i]]];
    
16.     AppendTo[y, fy[t1, t20, h0] /. sol[[i]]];
    
17.     AppendTo[z, fz[t1, t20, h0] /. sol[[i]]]];(*End For*)
    
18.    pts = Table[{t1 /. sol[[i]], x[[i]], y[[i]], z[[i]]} // N, {i, n}],
    
19.    pts = {}]; (*End If*)
    
20.   (*输出计算结果*)
    
21.   pts
    
22.   ](*End Module*)

复制代码

计算步骤：
1. 给定 h 参数，一个 t2 参数对应相交曲线上 0 个或多个点。
2. 令 \(f_{x1a}\) 和 \(f_{x2a}\) 相等求出 t1
3. 计算 \(f_{x1a}\) 和 \(f_{x2a}\) 的平均值作为 x 坐标（也可以只取其中之一）。
4. 用 \(f_y\) 和 \(f_z\) 分别计算 y、z 坐标。

Jack315

在 \((0,2\pi)\) 内均匀取 120 个 t2 值：

1. t2 = Table[(i - 1)/120 2 \[Pi], {i, 120}];

复制代码

计算交线上点坐标：

1. data = Table[getPoints[t2[[i]], 500], {i, Length[t2]}];
   
2. pts = Table[Table[data[[i, j, 2 ;; 4]], {j, Length[data[[i]]]}], {i, Length[data]}] // Flatten;
   
3. Length[pts]
   
4. pts = ArrayReshape[pts, {232, 3}];

复制代码

画图：

1. ListPointPlot3D[pts, PlotStyle -> Red]
   
2. 
   
3. Show[{ParametricPlot3D[{{fx1[k, t], fy1[k, t], fz1[k, t]},
   
4. {fx2[k, t], fy2[k, t], fz2[k, t]} /. h -> 500}, {k, 0.75, 1.25}, {t, 0, 2 \[Pi]}],
   
5.   ListPointPlot3D[pts, PlotStyle -> Cyan]}]

复制代码

Jack315

从图上看，很可能是两个椭圆。
虽然直接求解参数方程有困难，但根据求出的点拟合出参数方程还是有可能的。