两参数曲面的相交曲线计算问题

lihpb00

这种有两条曲线相交而成的曲线应该不存在标准的解析式吧，可能只有对应的数值解

Jack315

下一步，看能否给双椭圆台相交曲线的参数方程？

在椭圆台参数方程中令 \(\sin{\theta}=t\)，则 \(\cos{\theta} =\pm\sqrt{1-t^2}\) ，即将椭圆台分成两半。
然后用相同的方法求解双椭圆台相交曲线的参数方程。
CPU 跑了 N 分钟后给出了结果。表达式很长很长。
俺的 CPU 是跑不动了，LZ 如果有资源可以自己试试。

Jack315

两个椭圆台的相交线位于两个平面上，因此可以改成求一个椭圆台与两个平面的相交线：
1. 用数值方法求出相交线上点的坐标。
2. 用得到的点坐标数据拟合平面。
3. 求椭圆台与两个平面相交线的参数方程。

这是取 \(h_{22}=500\) 时两个相交线的参数方程：
\(\begin{cases}
fx(t)=\frac{\cos{t}(23082.3-759.109\sin{t})-3.63798\times 10^{-12}\sin{t}}{(-15.2036+\cos{t})(-30.4071+\sin{t})}\\
fy(t)=\frac{(27705.3-911.144\sin{t})\sin{t}+\cos{t}(3.63798\times 10^{-12}-304.071\sin{t}+10\sin^2{t})}{(-15.2036+\cos{t})(-30.4071+\sin{t})}\\
fz(t)=\frac{-1083.67+\cos{t}(50678.5-1666.67\sin{t})+35.6388\sin{t}}{(-15.2036+\cos{t})(-30.4071+\sin{t})}
\end{cases}\)

\(\begin{cases}
fx(t)=\frac{-2.27374\times 10^{-13}\sin^2{t}+\cos{t}(102565+1600\sin{t}-2.66454\times 10^{-15}\sin^2{t})}{(32.0515+\cos{t}+2.22045\times 10^{-16}\sin{t})(64.103+\sin{t})}\\
fy(t)=\frac{\sin{t}[123111+1920.51\sin{t}+\cos{t}(641.03+10\sin{t})]}{(32.0515+\cos{t}+2.22045\times 10^{-16}\sin{t})(64.103+\sin{t})}\\
fz(t)=\frac{-5512.43+\cos{t}(-106838-1666.67\sin{t})-85.9934\sin{t}-2.27374\times 10^{-13}\sin^2{t}}{(32.0515+\cos{t}+2.22045\times 10^{-16}\sin{t})(64.103+\sin{t})}
\end{cases}
\)

可视化验证：


这是 Mathematica 代码文件供参考：
参数方程.rar (24.96 KB, 下载次数: 1)

2024-7-27 21:11 上传

点击文件名下载附件

文档中画的图在保存前已被删除以压缩文件大小。重新计算一遍就可以得到这些图。

数学星空

根据楼上的计算对比知道，2#的方法是因为误认为\(t_1=t_2=t\)，所以算出来的不对

重新计算如下：

设两椭圆台曲面A和B的参数方程为：

[(-30*k1 + 80)*cos(t1), (-30*k1 + 90)*sin(t1), 1000 - 1000*k1],

[-500*(-1 + k2)*sqrt(3)/2 + 5*sin(t2)*(-8 + k2), (-10*k2 + 70)*cos(t2) + 30 - 30*k2, -5*sin(t2)*(-8 + k2)*sqrt(3) - 500*(-1 + k2)/2]

隐函数方程为：

(10000*y^2)/(9*(2000 + z)^2) + 10000*x^2/(5000 + 3*z)^2 - 1,

2500*(sqrt(3)*x - 3*z)^2/(sqrt(3)*z + 7000*sqrt(3) + 3*x)^2 + (100*sqrt(3)*y - 3*sqrt(3)*z - 9*x)^2/(sqrt(3)*z + 6000*sqrt(3) + 3*x)^2 - 1

由\(x_1=x_2,y_1=y_2,z_1=z_2\)消元得到：

[-1000*(13*cos(t2) - 3*sin(t1) - 15)*(9*cos(t1) + 100*sqrt(3))*cos(t1)/((30000 + 27*(cos(t2) + 3)*cos(t1)^2 + 10000*cos(t2) - 30000*sin(t1))*sqrt(3) + 1800*(cos(t2) - (3*sin(t1))/2 + 3)*cos(t1)),

9*(((cos(t2) + 3)*cos(t1)^2 - (40000*cos(t2))/9 + 20000/3)*sqrt(3) + cos(t1)*(-(1100*cos(t2))/3 + 700))*sin(t1)/(10*((cos(t2) - 3*sin(t1) + 3)*sqrt(3) + (9*cos(t1)*(cos(t2) + 3))/100)*(sqrt(3)*cos(t1) + 100/3)),

(((-45000*cos(t2) - 135000)*cos(t1)^2 - 60000000*cos(t2) + 60000000*sin(t1))*sqrt(3) - 6900000*(cos(t2) - (18*sin(t1))/23 + 15/23)*cos(t1))/(300*((cos(t2) - 3*sin(t1) + 3)*sqrt(3) + (9*cos(t1)*(cos(t2) + 3))/100)*(sqrt(3)*cos(t1) + 100/3))]

其中约束方程为：

sin(t2) = 50*(-5600*cos(t1)*(cos(t2) - (51*sin(t1))/56 + 15/14)*sqrt(3) + 9*(-60 - 2*cos(t2) - 3*sin(t1))*cos(t1)^2 - 180000*cos(t2) + 180000*sin(t1))/((210000 + 27*(21 + cos(t2) + sin(t1))*cos(t1)^2 + 10000*cos(t2) - 150000*sin(t1))*sqrt(3) + 1800*cos(t1)*(cos(t2) - 7*sin(t1) + 21))

画图得到相交曲线图像：




将曲面A,B和相交曲线图像得到：



显然相交曲线计算的不完整，可能是因为约束方程的数值计算还要优化一下

现在剩下的问题是如何简化约束方程，使参数表达更简洁？是否有其它的更简洁的表达方案（参数方程）？

Jack315

“标准椭圆”参数方程：
\(\begin{cases}
f_x(t)=a\cos(t)\\
f_y(t)=b\sin(t)\\
f_z(t)=0
\end{cases}\)

将上述椭圆曲线绕 y 轴旋转一个角度 \(\theta\)，然后再移位
就能得到所需的椭圆台相交曲线的参数方程。
所以应该有“标准”的参数方程形式，或许更简洁。

参考：三维坐标变换--旋转矩阵与旋转向量
https://blog.csdn.net/mightbxg/article/details/79363699
\(\begin{array}{cc}
R_x=\begin{pmatrix}1&0&0\\0&\cos\theta&-\sin\theta\\0&\sin\theta&\cos\theta\end{pmatrix}&
R_y=\begin{pmatrix}\cos\theta&0&\sin\theta\\0&1&0\\-\sin\theta&0&\cos\theta\end{pmatrix}&
R_z=\begin{pmatrix}\cos\theta&-\sin\theta&0\\\sin\theta&\cos\theta&0\\0&0&1\end{pmatrix}
\end{array}\)

Jack315

用三角函数级数拟合得到的参数方程：
\(\begin{cases}
fx(t)=2.1537+50.1492\sin(1.0021t-0.0075)+1.1724\sin(1.9642t-1.3388)\\
fy(t)=-0.0549+60.0152\sin(1.0009t+1.5679)+0.9832\sin(2.0004t+0.0364)\\
fz(t)=2.3816+109.8762\sin(1.0006t-0.0021)+1.8069\sin(1.9895t-1.4882)
\end{cases}\)

\(\begin{cases}
fx(t)=-1.5424-49.972sin(1.0010t+43.9793)\\
fy(t)=0.0092+59.9685\sin(0.9998t+1.5713)+0.1729\sin(2.0062t-3.1244)\\
fz(t)=-1.0723+51.8990\sin(0.9987t+0.0052)+0.2599\sin(1.8436t-3.8483)
\end{cases}\)

拟合参数方程中二次谐波的出现，意味着曲线不是完全在一个平面上。
只是与基频比较，系数小了约一个数量级，所以看起来像是在一个平面上。

另外，用 Chebyshev 多项式拟合也是一个可能的选项，近似计算可能会更方便。

mathe

看起来像在一个平面是因为两个图看起来像两个椭圆锥相交，而且椭圆的长短轴位置对应在一起。对于这种情景，查看过四个相交在一起的长短轴顶点的平面，可以知道这个平面割两个椭圆锥的结果都是椭圆，而且这个相交出来的椭圆长短轴相等，得到两个椭圆轨迹重叠；所以两者相交在这个平面上。

Jack315

使用切比雪夫多项式拟合三角函数时，从拟合精度角度看，宜选择
第一类切比雪夫多项式 \(ChebyshevT(n,x)\) 拟合 \(\sin(x)\) 函数。
相关数据如下表所示：
\(\begin{array}{|c|c|c|}
\hline T(n,x)\text{ 的 }n\text{ 参数}&\text{多项式项数}&\text{拟合 }\sin(x)\text{ 的最大误差}\\
\hline 3&2&0.020017\\
\hdashline 5&3&0.007117\\
\hdashline 7&4&0.003619\\
\hdashline 9&5&0.002186\\
\hdashline 11&6&0.001462\\
\hdashline 13&7&0.001047\\
\hdashline 15&8&0.000786\\
\hdashline ...&...&...\\
\hdashline 43&22&0.000096\\
\hline \end{array}\)

用第一类切比雪夫多项式 \(ChebyshevT(13,x)\) 拟合 \(\sin(x)\) 的函数如下：

1. ChebyshevTSin[x_] := Module[
   
2.   {sol, r, a, t, sign},
   
3.   
   
4.   sol = NSolve[D[ChebyshevT[13, r], r] == 0, r] // Sort;
   
5.   a = r /. sol[[7]];
   
6.   
   
7.   t = Mod[Abs[x], 2 \[Pi]];
   
8.   (*确定正弦函数值的符号*)
   
9.   sign = Sign[x] If[0 < t < \[Pi], 1, -1];
   
10.   
    
11.   (*将 t 移到 [0,\[Pi]/2] 范围内对应的位置*)
    
12.   t = (2 a)/\[Pi] If[t < \[Pi]/2, t,
    
13.      If[t < \[Pi], \[Pi] - t,
    
14.       If[t < (3 \[Pi])/2, t - \[Pi], 2 \[Pi] - t]]];
    
15.   
    
16.   (*输出拟合值*)
    
17.   sign  ChebyshevT[13, t]
    
18.   ](*End Module*)

复制代码

将 \(ChebyshevTSin(x)\) 作为 \(\sin(x)\) 代入 16# 的公式即可。

数学星空

关于两个一般椭圆台曲面相交的计算，现遇到两个很麻烦的计算问题需要探讨一下：

对第一个椭圆台方程：

[(k1*a11 + (1 - k1)*a12)*cos(t1) + k1*x0, (k1*b11 + (1 - k1)*b12)*sin(t1) + k1*y0, k1*H11 - (1 - k1)*H12]

与第一个垂直椭圆台方程：

[k2*H21 - (1 - k2)*H22, (k2*b21 + (1 - k2)*b22)*sin(t2), (k2*a21 + (1 - k2)*a22)*cos(t2)]

将第二个椭圆台曲面旋转60度，且其它相关参数

[a11 = 50, b11 = 60, a12 = 80, b12 = 90, a21 = 60, b21 = 70, x0 = 30, y0 = 50, a22 = 70, b22 = 80, t0 = Pi/6, H11 = 500, H12 = 500, H21 = 500, H22 = 500]

我们可以算出两椭圆台曲面的截交曲线方程：

[(-30*((sin(t1) - sin(t2) + 40/3)*cos(t1) - 9*sin(t1) + sin(t2))*cos(t2)*sqrt(3) + (3000*sin(t1) - 9500*sin(t2) + 40000)*cos(t1) - 27000*sin(t1) + 25500*sin(t2))/(cos(t2)*(3*sin(t1) - 5)*sqrt(3) - 300*sin(t1) + 200*sin(t2) + 500), 30*sin(t2)*(cos(t2)*(sin(t1) - 5/3)*sqrt(3) - 250*sin(t1) + 4250/3)/(cos(t2)*(3*sin(t1) - 5)*sqrt(3) - 300*sin(t1) + 200*sin(t2) + 500), (7500*cos(t2)*(sin(t1) - (2*sin(t2))/15 + 1/3)*sqrt(3) - 750000*sin(t1) + 750000*sin(t2) - 250000)/(cos(t2)*(3*sin(t1) - 5)*sqrt(3) - 300*sin(t1) + 200*sin(t2) + 500)] ......(1)

且t1,t2 需要满足如下方程：

((1500*cos(t2)*sqrt(3) - 150000)*sin(t1) - 1500*cos(t2)*sqrt(3)*sin(t2) + 20000*cos(t2)*sqrt(3) + 475000*sin(t2) - 2000000)*cos(t1) + (-13500*cos(t2)*sqrt(3) - 37500000*sqrt(3) + 1575000*cos(t2) + 1350000)*sin(t1) + 1500*cos(t2)*sqrt(3)*sin(t2) + 37500000*sin(t2)*sqrt(3) + 50000*cos(t2)*sin(t2) - 12500000*sqrt(3) - 3375000*cos(t2) - 1275000*sin(t2)=0 ...........................................(2)

利用数学软件MAPLE可以算出：

两个椭圆台曲面及截交曲线如下图：



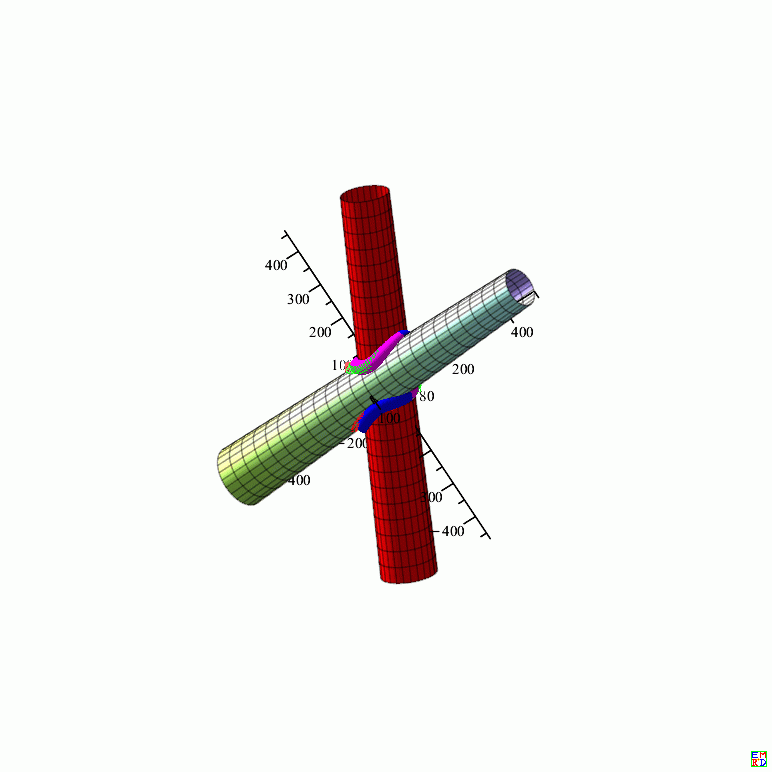
截交曲线如下图：



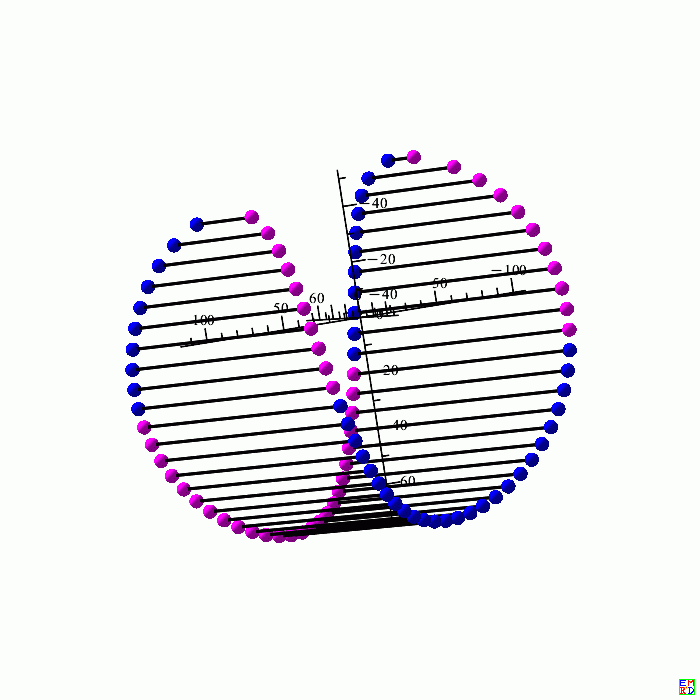
（2）的隐函数方程图像如下：




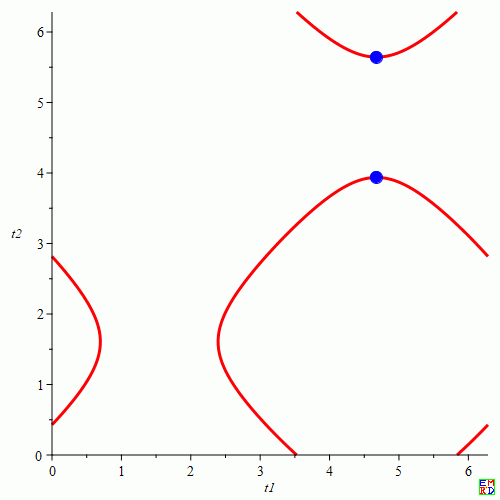
现在主要的难题在于如何快速高效的计算下式：（例如本例（2）式）

\((m_1\cos(t_2) + m_0)\sin(t_1)\cos(t_1) + (n_1\cos(t_2)\sin(t_2) + n_2\cos(t_2) + n_3\sin(t_2) + n_0)\cos(t_1) + (p_1\cos(t_2) + p_0)\sin(t_1) + q_1\cos(t_2)\sin(t_2) + q_2\cos(t_2) + q_3\sin(t_2) + q_0=0\)....................................(3)

其中 \(m_1,m_2,m_0,n_1,n_2,n_3,n_0,p_0,p_1,q_1,q_2,q_3,q_0\)为已知常数

A. 若已知\( t_2 (0<t_2<2\pi)\),求\( t_1 (0<t_1<2\pi) \)?

B.\(t_1,t_2\) 满足 (3) 如何求\(t_2\)的两个顶点（上面最后一个截图中的两个蓝色点坐标）

对于只有简单计算功能（加，减，乘，除，三角函数，log，exp；无代数方程及积分等高级的计算功能)的参数化平台,如何利用数值计算来解决A,B问题

注：

显然对A问题，利用牛顿迭代计算公式\(x_{k+1}=x_{k}-\frac{f(x)}{f'(x)}\)可以解决 ,请结合函数的性质，选择合适的 \(f(x)\), 给出高效的迭代计算公式（要求6次迭代给出至少10^(-4)的计算精度）

由于\(t_2\) 已知代入（3）可以得到 \( A\sin(t_1)\cos(t_1)+B\cos(t_1)+C\sin(t_1)+D=0\)， f(x)可以有如下选择，不知哪个最优

1. \(f(x)=\arcsin(\frac{B\cos(x)+D}{A\cos(x)+C})\)

2. \(f(x)=\arccos(\frac{C\sin(x)+D}{A\sin(x)+B})\)

3. \(f(x)=-\frac{1}{2}\arcsin(\frac{B\cos(x)+C\sin(x)+D}{A})\)

......

显然对B问题，利用数学软件可以有办法计算 \(F(t_1,t_2)=0,F'(t_1,t_2)=0\) 可以计算出两个顶点的坐标），但脱离数学软件不知有什么数值计算方法来得到这两个顶点的坐标？

mathe

计算问题其实挺无聊的。
对于解方程\(A \cos(t)\sin(t)+B\cos(t)+C\sin(t)+D=0\)
不如转化为多项式求解问题，先把方程写成
\((A\sin(t)+B)\cos(t)=-C\sin(t)-D\)两边同时平方并且把\(\cos^2(t)\)替换为\(1-\sin^2(t)\),就变成\(\sin(t)\)的多项式了。

第二个问题由于是看成$t_2$关于$t_1$的隐函数\(F(t_1,t_2)=0\)的极值问题，所以我们需要寻找\(\frac{dt_2}{dt_1}=0\)的点
由于\(\frac{\partial F}{\partial t_2}\frac{dt_2}{dt_1}+\frac{\partial F}{\partial t_1}=0\), 所以我们实际上需要解方程组
\(\begin{cases}F(t_1,t_2)=0\\\frac{\partial F(t_1,t_2)}{\partial t_1}=0\end{cases}\)
这个题目里面就转化为关于$t_1,t_2$的三角函数的方程组求解问题。同样我们不喜欢三角函数，可以通过万能公式全部转化为
\(\tan(\frac{t_1}2),\tan(\frac{t_2}2)\)的多项式方程组。然后用软件就比较容易求解了。