关于三角形的几个问题

数学星空

以下是数值计算的具体实例：

$B$点为原点，$A$点为顶点，$C$点位于x轴正半轴，$a,b,c$为三角形$ABC$三边长，
$ A(x1,y1), B(x2,y2), C(x3,y3), P(x0,y0), PA=x, PB=y, PC=z,  PD=d1, PE=d2, PF=d3 $  (点$P$到三边的距离）,
$ (x01,y01,r), (x02,y02,r), (x03,y03,r) $分别为三个内切圆的圆心坐标及半径


1.${a = 5, b = 12, c = 8, d1 = 1.229952893, d2 = 1.126154433, d3 = 1.172969680, r = .5579288175, x = 7.508945269, x0 = .4508181064, x01 = .7987251904, x02 = .7033301478, x03 = -.2139430191, x1 = -5.500000000, x2 = 0, x3 = 5, y = 1.309969879, y0 = 1.229952893, y01 = .5579288176, y02 = 1.739642892, y03 = 1.037514030, y1 = 5.809475019, y2 = 0, y3 = 0, z = 4.712519498}
$

J01

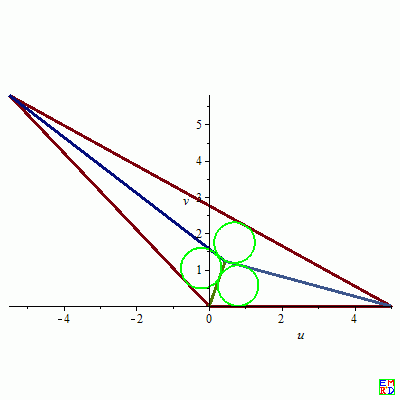
2.${a = 5, b = 12, c = 9, d1 = 1.689506089, d2 = 1.517203753, d3 = 1.570908960, r = .7457030106, x = 8.023198840, x0 = .9460222550, x01 = 1.272195270, x02 = 1.424479787, x03 = 0.6097890397e-1, x1 = -3.800000000, x2 = 0, x3 = 5, y = 1.936333889, y0 = 1.689506088, y01 = .7457030105, y02 = 2.297977229, y03 = 1.635219712, y1 = 8.158431222, y2 = 0, y3 = 0, z = 4.391943349}
$

J02

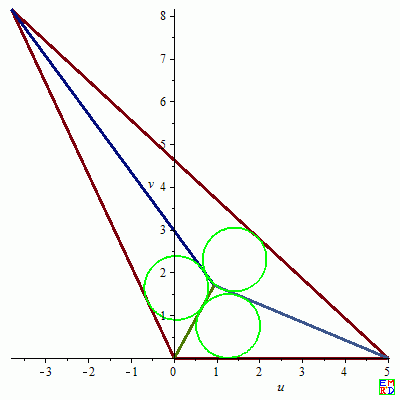
3.${a = 5, b = 12, c = 10, d1 = 1.981057659, d2 = 1.761790957, d3 = 1.804242474, r = .8598979637, x = 8.524477990, x0 = 1.454333527, x01 = 1.698003216, x02 = 2.129557975, x03 = .4705899128, x1 = -1.900000000, x2 = 0, x3 = 5, y = 2.457575118, y0 = 1.981057660, y01 = .8598979636, y02 = 2.588806893, y03 = 2.094106705, y1 = 9.817840903, y2 = 0, y3 = 0, z = 4.061568686}
$

J03

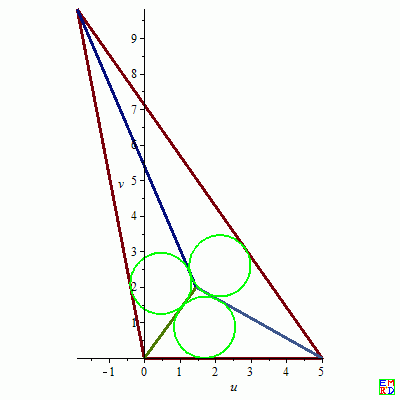
4.${a = 5, b = 12, c = 11, d1 = 2.158700984, d2 = 1.910836114, d3 = 1.933397275, r = .9270860023, x = 9.015533833, x0 = 1.972972523, x01 = 2.103285276, x02 = 2.809835590, x03 = .9715595778, x1 = .2000000000, x2 = 0, x3 = 5, y = 2.924484659, y0 = 2.158700985, y01 = .9270860009, y02 = 2.700582090, y03 = 2.437213571, y1 = 10.99818167, y2 = 0, y3 = 0, z = 3.717914105}
$

J04

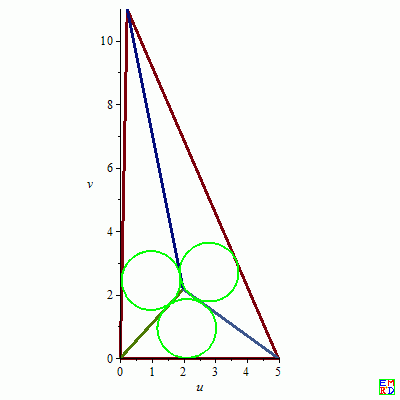
5.${a = 5, b = 12, c = 12, d1 = 2.237793560, d2 = 1.978937715, d3 = 1.978937715, r = .9554641421, x = 9.498901032, x0 = 2.500000000, x01 = 2.499999999, x02 = 3.455464143, x03 = 1.544535859, x1 = 2.500000000, x2 = 0, x3 = 5, y = 3.355252602, y0 = 2.237793561, y01 = .9554641409, y02 = 2.664870375, y03 = 2.664870379, y1 = 11.73669459, y2 = 0, y3 = 0, z = 3.355252602}
$

j05

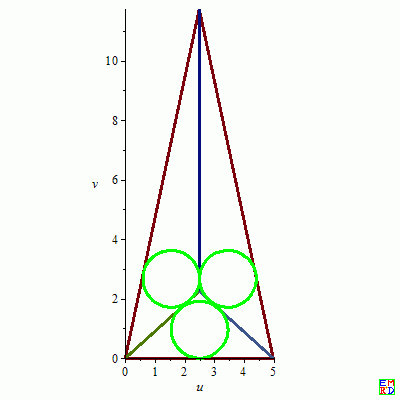
6.${a = 5, b = 12, c = 13, d1 = 2.218896004, d2 = 1.967039709, d3 = 1.946234112, r = .9463673765, x = 9.976935430, x0 = 3.032960291, x01 = 2.896357472, x02 = 4.053632624, x03 = 2.177615229, x1 = 5.000000000, x2 = 0, x3 = 5, y = 3.757971209, y0 = 2.218896005, y01 = .9463673753, y02 = 2.494160414, y03 = 2.765721369, y1 = 12.00000000, y2 = 0, y3 = 0, z = 2.965256262}$

j06

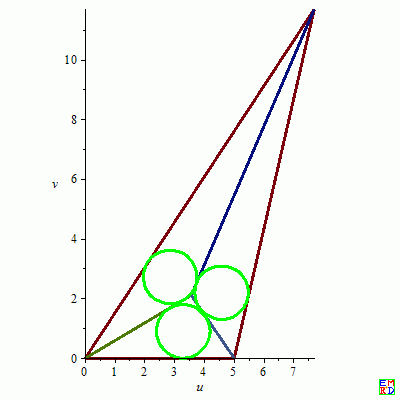
7$.{a = 5, b = 12, c = 14, d1 = 2.091407270, d2 = 1.865736630, d3 = 1.829689279, r = .8960239863, x = 10.45225892, x0 = 3.568114696, x01 = 3.300627212, x02 = 4.586216383, x03 = 2.861320816, x1 = 7.700000000, x2 = 0, x3 = 5, y = 4.135870749, y0 = 2.091407269, y01 = .8960239856, y02 = 2.190445749, y03 = 2.715727316, y1 = 11.69230516, y2 = 0, y3 = 0, z = 2.534616320}$

j07

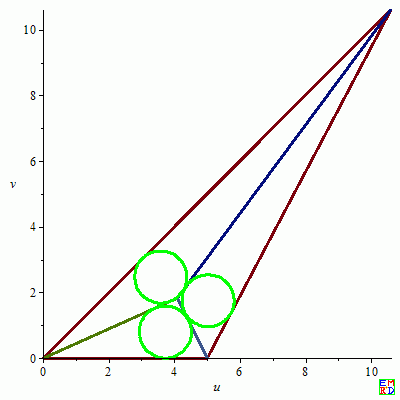
8$.{a = 5, b = 12, c = 15, d1 = 1.828312687, d2 = 1.650087498, d3 = 1.608225550, r = .7930888457, x = 10.92873470, x0 = 4.098999404, x01 = 3.724999407, x02 = 5.024123199, x03 = 3.585514735, x1 = 10.60000000, x2 = 0, x3 = 5, y = 4.488265076, y0 = 1.828312687, y01 = .7930888459, y02 = 1.745194724, y03 = 2.467683952, y1 = 10.61319933, y2 = 0, y3 = 0, z = 2.038266262}
$

j08

数学星空

将以上8个实例的相关参数代入16#并不成立，有谁也帮忙验算一下？？

即  $d1:d2:d3=1/{cos(B/2)+cos(C/2)-cos(A/2)}:1/{cos(A/2)+cos(C/2)-cos(B/2)}:1/{cos(B/2)+cos(A/2)-cos(C/2)}$

或者 $d1:d2:d3={1+sin(B/2)+sin(C/2)-sin(A/2)}:{1+sin(A/2)+sin(C/2)-sin(B/2)}:{1+sin(B/2)+sin(A/2)-sin(C/2)}$

或者 $d1:d2:d3={sin(A/2)/cos(A/2)-1/cos(A/2)}:{sin(B/2)/cos(B/2)-1/cos(B/2)}:{sin(C/2)/cos(C/2)-1/cos(C/2)}$

creasson

第二问:
仿射坐标得：
以21#之例一为例,a=5,b=12,c=8,求得半径为:
Root[10509453369140625 - 101065131421875000 #1^2 + 364215132497250000 #1^4 - 603416863332864000 #1^6 + 446275689775543296 #1^8 - 115900798939201536 #1^10 +
   9004687219228672 #1^12 - 111502367391744 #1^14 + 347892350976 #1^16 &, 9]
=0.5579288174552170449363194990668352258046949085789545108583825974015618689493773557697611062006268629

creasson

数学星空

TO   cresson :
你23#的方程组还没有13#方程组简洁，在这里并不具备什么优势，你可以试着看能否给出最终的方程（关于圆半径与a,b,c）??

数学星空

例如：

将以上第1个实例的相关参数代入16#

即   $d1:d2:d3=1.229952893：1.126154433：1.172969680＝1.000000000：0.9156077760：0.9536704102$

$1/{cos(B/2)+cos(C/2)-cos(A/2)}:1/{cos(A/2)+cos(C/2)-cos(B/2)}:1/{cos(B/2)+cos(A/2)-cos(C/2)}＝2.664401745：0 .6405440431：2.408184130

＝1.000000000：0.2404082058：0.9038367185$

${1+sin(B/2)+sin(C/2)-sin(A/2)}:{1+sin(A/2)+sin(C/2)-sin(B/2)}:{1+sin(B/2)+sin(A/2)-sin(C/2)}＝2.015465545：0.4845344553：1.821651763

＝1.000000000：0.2404082057：0.9038367178$

${sin(A/2)/cos(A/2)-1/cos(A/2)}:{sin(B/2)/cos(B/2)-1/cos(B/2)}:{sin(C/2)/cos(C/2)-1/cos(C/2)}＝-0.8570095172：-0.206032119：-0.7745966692

＝1.000000000：0.2404082042：0.9038367179$

有谁再帮忙验算一下以上计算是否有误？？

或者有谁能提供相关研究的资料：CONGRUENT INCIRCLES ISOSCELIZER POINT  (M. Iliev, 4/12/07)

数学星空

若要求三角形内接三个相互外切的圆（半径分别为 \(r_1,r_2,r_3 \)),且每个圆与三角的两边相切，则

\(2\left( r_1*\cot\frac A2+r_2*\cot\frac B2+r_3*\cot\frac C2+\sqrt{r_1*r_2}+\sqrt{r_2*r_3}+\sqrt{r_3*r_1} \right)=a+b+c \)

即 \(s(r-r_1-r_2-r_3)=r\left( \sqrt{r_1*r_2}+\sqrt{r_2*r_3}+\sqrt{r_3*r_1} \right)-(a*r_1+b*r_2+c*r_3) \)

当 \(r_1=r_2=r_3 \) 时 \( r_0=\dfrac{s*r}{3r+s} \)   \(r_0=r_1=r_2=r_3 \) 注 \(s=\dfrac{a+b+c}2 \)为半周长， \(r=S/s \)为三角形内切圆半径，

\(S=\dfrac{\sqrt{2*a^2*b^2+2*a^2*c^2+2*b^2*c^2-a^4-b^4-c^4}} 4 \)为三角形面积，

\[\begin{split} r&=\frac s {\cot\frac A2+\cot\frac B2+\cot\frac C2+3}=\frac{s S}{s^2+3 S}\\
&=\frac{(a+b+c)*\sqrt{2*a^2*b^2+2*a^2*c^2+2*b^2*c^2-a^4-b^4-c^4}}{2*\left( (a+b+c)^2+3*\sqrt{2*a^2*b^2+2*a^2*c^2+2*b^2*c^2-a^4-b^4-c^4} \right)} \end{split}  \]

数学星空

第二幅图引自：http://bbs.cnool.net/cthread-64820690.html

数学星空

当 \( s \) 点为 \( \triangle ABC \) 的内心时
1.即28# 第一列的第3幅图有( \( s,S,r \) 的含义同27#)
\[\begin{split} r_1:r_2:r_3&=\frac{r}{1+\tan(A/2)}:\frac{r}{1+\tan(B/2)}:\frac{r}{1+\tan(C/2)}\\
&=\frac{S(s-a)}{s(s-a)+S}:\frac{S(s-b)}{s(s-b)+S}:\frac{S(s-c)}{s(s-c)+S}\\
&=\frac{(s-a)\sqrt{(s-b)(s-c)}}{\sqrt{s(s-a)}+\sqrt{(s-b)(s-c)}}:\frac{(s-b)\sqrt{(s-a)(s-c)}}{\sqrt{s(s-b)}+\sqrt{(s-a)(s-c)}}:\frac{(s-c)\sqrt{(s-a)(s-b)}}{\sqrt{s(s-c)}+\sqrt{(s-a)(s-b)}}\end{split} \]

数学星空

当 \( s \) 点为 \( \triangle ABC \) 的内心时
1.即28# 第一列的第2幅图有( \( s,S,r \) 的含义同27#)
\[\begin{split} r_1:r_2:r_3&=\frac{a}{\frac{1}{\sin\frac B2}+\frac{1}{\sin\frac C2}+\frac{1}{\cot\frac B2+\cot\frac C2}}:\frac{b}{\frac{1}{\sin\frac A2}+\frac{1}{\sin\frac C2}+\frac{1}{\cot\frac A2+\cot\frac C2}}:\frac{c}{\frac{1}{\sin\frac A2}+\frac{1}{\sin\frac B2}+\frac{1}{\cot\frac A2+\cot\frac B2}}\\
&=\frac{a}{\frac{1}{\sin\frac B2}+\frac{1}{\sin\frac C2}+\frac{\sin\frac B2\sin\frac C2}{\cos\frac A2}}:\frac{b}{\frac{1}{\sin\frac A2}+\frac{1}{\sin\frac C2}+\frac{\sin\frac A2\sin\frac C2}{\cos\frac B2}}:\frac{c}{\frac{1}{\sin\frac A2}+\frac{1}{\sin\frac B2}+\frac{\sin\frac A2\sin\frac B2}{\cos\frac C2}}\\
&=\frac{a}{\sqrt{\frac{a}{s-a}}\left( \sqrt{\frac{b}{s-b}}+\sqrt{\frac{c}{s-c}} \right)+\frac{r}{a}}:\frac{b}{\sqrt{\frac{b}{s-b}}\left( \sqrt{\frac{a}{s-a}}+\sqrt{\frac{c}{s-c}} \right)+\frac{r}{b}}:\frac{c}{\sqrt{\frac{c}{s-c}}\left( \sqrt{\frac{a}{s-a}}+\sqrt{\frac{b}{s-b}} \right)+\frac{r}{c}}\end{split} \]