椭圆内接N等边及N等角凸边形问题

wayne

nice. 跟我提供的动画的 几个图样 还是很一致的.
看来咱俩都没算错.

数学星空

对于$N=4$,我们得到如下结论，内接等边长$L_max= sqrt(a^2+b^2), L_min={2*b*a}/sqrt(a^2+b^2),$包络曲线为圆且半径$ r = {b*a}/sqrt(a^2+b^2)$
具体计算实例，取$a=5,b=3$得到

最大等边长与最小等边长分别见红色和绿色四边形


下图中黑色圆即为包络曲线


奇怪的是楼上消元得到的（5）分别令$L=5.15,5.2,5.3,5.4,5.5,5.6,5.7,5.8$得到的包络曲线和黑色的圆并不重合？？？  （有谁能解释一下呢）

mathe

也就是说不同起始位置的等边多边形边长不同了？那两曲线自然不同

数学星空

对于$N=5$,我们得到等边长$L_max$与$L_min$分别满足下面两个方程 （最小正实根）


$1310720*a^12*b^16+2621440*a^10*b^18+1310720*a^8*b^20+(a^20+46*a^18*b^2+741*a^16*b^4+4456*a^14*b^6+1586*a^12*b^8-44140*a^10*b^10+48610*a^8*b^12+13800*a^6*b^14-31475*a^4*b^16+750*a^2*b^18+
5625*b^20)*L^8+(-336*a^18*b^4-6528*a^16*b^6-22976*a^14*b^8+136064*a^12*b^10+170272*a^10*b^12-450176*a^8*b^14-16320*a^6*b^16+208000*a^4*b^18-18000*a^2*b^20)*L^6+(22272*a^16*b^8-90624*a^14*b^10-511744*a^12*b^12+443392*a^10*b^14+1788160*a^8*b^16-442880*a^6*b^18-160000*a^4*b^20)*L^4+(266240*a^14*b^12-81920*a^12*b^14-2990080*a^10*b^16-2703360*a^8*b^18+266240*a^6*b^20)*L^2＝0$


$1310720*a^20*b^8+2621440*a^18*b^10+1310720*a^16*b^12+(5625*a^20+750*a^18*b^2-31475*a^16*b^4+13800*a^14*b^6+48610*a^12*b^8-44140*a^10*b^10+1586*a^8*b^12+4456*a^6*b^14+741*a^4*b^16+
46*a^2*b^18+b^20)*L^8+(-18000*a^20*b^2+208000*a^18*b^4-16320*a^16*b^6-450176*a^14*b^8+170272*a^12*b^10+136064*a^10*b^12-22976*a^8*b^14-6528*a^6*b^16-336*a^4*b^18)*L^6+
(-160000*a^20*b^4-442880*a^18*b^6+1788160*a^16*b^8+443392*a^14*b^10-511744*a^12*b^12-90624*a^10*b^14+22272*a^8*b^16)*L^4+(266240*a^20*b^6-2703360*a^18*b^8-
2990080*a^16*b^10-81920*a^14*b^12+266240*a^12*b^14)*L^2＝0$

具体的计算实例见下图

取$a=5,b=3$,得到最大和最小的内接等五边形


等五边形所形成的包络线与（5）求得的曲线是一致的（见黑色曲线）


分别令$L=4.6,4.615,4.616,4.617,4.617$得到的曲线重合成一条曲线（此结果正是我们需要的，但$N=4$为什么会不一致呢）

数学星空

对于$N=6$.我们得到如下结果：等边长$L_max=2*a*(a^2+b^2)/(3*a^2+b^2),L_min=2*b*(a^2+b^2)/(a^2+3*b^2)$

具体的计算实例见下图 （$a=5,b=3$)

内接最大和最小的等六边形


在（5）中分别取$L=3.93,3.97,4.02,4.04$得到的包络曲线也重合为一条曲线

数学星空

对于$N=8$,我们得到最大和最小的等边长$L_max,L_min$分别满足下列两个方程（取最小正实根）

$(16*a^8+32*a^4*b^4+16*b^8)*L^4+(-8*a^10-40*a^8*b^2-80*a^6*b^4-80*a^4*b^6-40*a^2*b^8-8*b^10)*L^2+a^12+10*b^2*a^10+31*a^8*b^4+44*a^6*b^6+31*a^4*b^8+10*b^10*a^2+b^12＝0
$

$(a^12+14*a^10*b^2+47*a^8*b^4+4*a^6*b^6+47*a^4*b^8+14*a^2*b^10+b^12)*L^4+(-8*a^12*b^2-72*a^10*b^4-176*a^8*b^6-176*a^6*b^8-72*a^4*b^10-8*a^2*b^12)*L^2+16*b^12*a^4+64*b^10*a^6+16*b^4*a^12+96*b^8*a^8+64*b^6*a^10＝0$

具体的计算实例见下图（$a=5,b=3$）

内接最大和最小的等八边形


分别取（5）中$L=3.06,3.07,3.08,3.09$得到的四条包络曲线重合为一条曲线


将以上的曲线画在一个坐标内得到

数学星空

对于椭圆\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b)\)内接等角\(N（\geqslant 5）\)边形，我们得到如下结论：
当椭圆\(\frac{a}{b}\in [\frac{1}{x_0},x_0]\)时,仅存在四个等角\(N(\geqslant 5)\)边形，且这4个等角形对称分布在椭圆左右或者上下两侧。

例\(N=5\)时


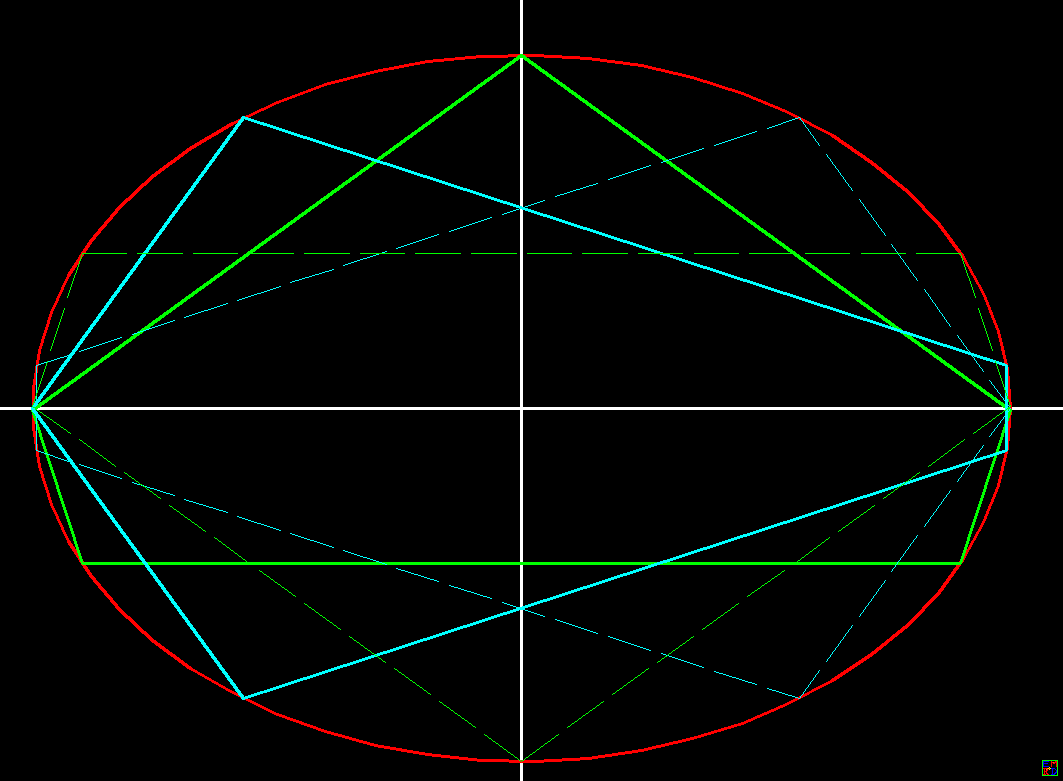
\(x_0=\frac{\sqrt{25+20\sqrt{5}}}{5}\)
设等角五边形各个顶点坐标依次为\(（0,-b）,(x_1,y_1),(x_2,y_2),(-x_2,y_2),(-x_1,y_1)\)[另一个关于X轴对称]，设各边长分别为\(L_1,L_2,L_3\),总长为\(L\),面积为\(S\)

\(  (-a^2k_1^2-b^2)x_1+2a^2bk_1＝0 \)
\(  (-a^2k_1^2-b^2)y_1^2-2b^3y_1+a^2b^2k_1^2-b^4＝0 \)
\(  (a^4k_1^2k_2^2+a^2b^2k_1^2+a^2b^2k_2^2+b^4)x_2+2a^4bk_1^2k_2-2a^4bk_1k_2^2+2a^2b^3k_1-2a^2k_2b^3＝0 \)
\( (a^4k_1^2k_2^2+a^2b^2k_1^2+a^2b^2k_2^2+b^4)y_2+a^4k_2^2k_1^2b-a^2k_1^2b^3+4a^2b^3k_1k_2-a^2b^3k_2^2+b^5＝0 \)

\(L_1^2-x_1^2-(b+y_1)^2=0\)
\(L_2^2-(x_1-x_2)^2-(y_1-y_2)^2=0\)
\(L_3=2x_2\)
\(L-2(L_1+L_2+x_2)=0\)

\(-51200a^8b^4n(a^2+b^2)(5a^6t-65a^4b^2t+79a^2b^4t-43b^6t+25a^6-85a^4b^2+235a^2b^4-103b^6)+1024a^6b^3(5a^4+10a^2b^2+b^4)(25a^6n^2t-25a^4b^2n^2t+75a^2b^4n^2t-19b^6n^2t+50a^6n^2-100a^4b^2n^2+170a^2b^4n^2-80b^6n^2+50a^6t+100a^4b^2t+250a^2b^4t-40b^6t-
125a^6-275a^4b^2-375a^2b^4+15b^6)L+320a^4b^2n(a^2+b^2)(5a^4+10a^2b^2+b^4)^2(3a^2t-b^2t+5a^2-15b^2)L^2-16a^2b(5a^4+10a^2b^2+b^4)^3(
2a^2n^2t+5a^2n^2-b^2n^2+5a^2t-b^2t-10a^2)L^3+n(5a^4+10a^2b^2+b^4)^4L^4=0\)

\(-n(5a^4+10a^2b^2+b^4)^2(20a^4t+4a^2b^2t-45a^4-10a^2b^2-b^4)S+20b^2a^4(325a^8t+580a^6b^2t+430a^4b^4t+68a^2b^6t+5b^8t-725a^8-1300a^6b^2-990a^4b^4-180a^2b^6-5b^8)=0\)

注：\(t=\sqrt{5},n=\sqrt{5-2\sqrt{5}},k_1=\sqrt{5-2\sqrt{5}},k_2=-\sqrt{5+2\sqrt{5}}\)

数学星空

设等角五边形各个顶点坐标依次为\(（a,0）,(x_2,y_2),(x_1,y_1),(x_1,-y_1),(x_2,-y_2)\)[另一个关于Y轴对称]，设各边长分别为\(L_1,L_2,L_3\),总长为\(L\),面积为\(S\)

\((-a^4k_1^2k_2^2-a^2b^2k_1^2-a^2b^2k_2^2-b^4)x_1+a^5k_1^2k_2^2-a^3b^2k_1^2-4a^3b^2k_1k_2-a^3b^2k_2^2+ab^4=0 \)
\(  (a^4k_1^2k_2^2+a^2b^2k_1^2+a^2b^2k_2^2+b^4)y_1+2a^3b^2k_1^2k_2+2a^3b^2k_1k_2^2-2ab^4k_1-2ab^4k_2=0\)
\(  (a^2k_2^2+b^2)x_2^2-2a^3k_2^2x_2+a^4k_2^2-a^2b^2=0\)
\( (a^2k_2^2+b^2)y_2-2ab^2k_2 =0 \)

\(L_1^2-(x_2-a)^2-y_2^2=0\)
\( L_2^2-(x_1-x_2)^2-(-y_2+y_1)^2=0\)
\(L_3=2y_1\)
\(L-2(L_1+L_2+y_1)=0\)

\(51200a^4b^8r(a^2+b^2)(43a^6t-79a^4b^2t+65a^2b^4t-5b^6t+103a^6-235a^4b^2+85a^2b^4-25b^6)-5120a^3b^6(a^4+10a^2b^2+5b^4)(53a^6t-175a^4b^2t+35a^2b^4t-25b^6t+145a^6-295a^4b^2+175a^2b^4-25b^6)L-320b^4a^2r(a^2+b^2)(a^4+10a^2b^2+5b^4)^2(a^2t-3b^2t+15a^2-5b^2)L^2+80ab^2(a^4+10a^2b^2+5b^4)^3(a^2t-3b^2t+3a^2-5b^2)L^3+r(a^4+10a^2b^2+5b^4)^4L^4=0\)

\(-(a^4+10a^2b^2+5b^4)^2(4a^4t+76a^2b^2t+360b^4t-9a^4-170a^2b^2-805b^4)S-20b^4a^2k_1(15a^8t+316a^6b^2t+1850a^4b^4t+2460a^2b^6t+1375b^8t-35a^8-700a^6b^2-4130a^4b^4-5500a^2b^6-3075b^8)=0\)

注：\(t=\sqrt{5},k_1=\frac{\sqrt{25-10\sqrt{5}}}{5},k_2=\frac{\sqrt{25+10\sqrt{5}}}{5},r=\sqrt{25+10\sqrt{5}}\)

葡萄糖

实际上问题：“椭圆内接N等边凸边形问题 ”可以化归为：椭圆上定长弦的包络曲线

wayne

数学星空 发表于 2014-1-24 20:40
我今天公布一下近几天计算的结果：

根据   /thread-5252-2-3.html  14#的计算及m ...

已经得到等边多边形的包络曲线的方程之后，对于给定的$a,b$,随便一个位置开始，画这个包络曲线$f(a,b,L)=0$的一个切线，然后其他的跟着就全部连起来了。你的22-26#都是这么来的吧