三角形两内点间距

数学星空

对以上结果作代换（\(5\sim7\) 结果不对称除外）

若做\(R,r,S\)代换得到：

1. \((4Rr+r^2-2S)^2(4Rr+r^2+2S)^2OJ^4+(-512R^6r^4-512R^5r^5-192R^4r^6-32R^3r^7-2R^2r^8+256R^4S^2r^2-176R^2S^2r^4-72RS^2r^5-8S^2r^6-32R^2S^4+32RS^4r+16S^4r^2)OJ^2+(16R^4r^2+8R^3r^3+R^2r^4+16R^3Sr-12R^2Sr^2-12RSr^3-2Sr^4+4R^2S^2-12RS^2r-4S^2r^2-2S^3)(16R^4r^2+8R^3r^3+R^2r^4-16R^3Sr+12R^2Sr^2+12RSr^3+2Sr^4+4R^2S^2-12RS^2r-4S^2r^2+2S^3)=0\)

2.  \(81r^4(4Rr+r^2-2S)^2(4Rr+r^2+2S)^2GJ^4+72r^2(1024R^5r^7+1280R^4r^8+640R^3r^9+160R^2r^{10}+20Rr^{11}+r^{12}-64R^4S^2r^4-672R^3S^2r^5-516R^2S^2r^6-136RS^2r^7-12S^2r^8+32R^2S^4r^2+104RS^4r^3+15S^4r^4-4S^6)GJ^2+16(64R^3r^5+48R^2r^6+12Rr^7+r^8+64R^2Sr^4+32RSr^5+4Sr^6-4R^2S^2r^2+8RS^2r^3-4RS^3r-4S^3r^2-S^4)(64R^3r^5+48R^2r^6+12Rr^7+r^8-64R^2Sr^4-32RSr^5-4Sr^6-4R^2S^2r^2+8RS^2r^3+4RS^3r+4S^3r^2-S^4)=0\)

3.  \(r^4(4Rr+r^2-2S)^2(4Rr+r^2+2S)^2HJ^4-8r^2(256R^6r^6+256R^5r^7+96R^4r^8+16R^3r^9+R^2r^10-192R^4S^2r^4-128R^3S^2r^5-44R^2S^2r^6-10RS^2r^7-S^2r^8+48R^2S^4r^2+16RS^4r^3+7S^4r^4-4S^6)HJ^2+(16(16R^4r^4+8R^3r^5+R^2r^6-16R^3Sr^3-12R^2Sr^4-6RSr^5-Sr^6+6RS^2r^3+3S^2r^4+4RS^3r-S^3r^2-S^4))(16R^4r^4+8R^3r^5+R^2r^6+16R^3Sr^3+12R^2Sr^4+6RSr^5+Sr^6+6RS^2r^3+3S^2r^4-4RS^3r+S^3r^2-S^4)=0\)

4.  \((4Rr+r^2-2S)^2(4Rr+r^2+2S)^2IJ^4-2r^2(16R^2r^2+8Rr^3+r^4+4S^2)(16R^2r^2+8Rr^3+r^4-3S^2)IJ^2+r^4(16R^2r^2+8Rr^3+r^4-3S^2)^2=0\)

8.  \(9(16R^2r^6+8Rr^7+r^8-8RS^2r^3-14S^2r^4+S^4)(4Rr+r^2-2S)^4FJ^4+6r^2(3072R^5r^7+3840R^4r^8+1920R^3r^9+480R^2r^{10}+60Rr^{11}+3r^{12}-3072R^4Sr^6-3072R^3Sr^7-1152R^2Sr^8-192RSr^9-12Sr^{10}-768R^4S^2r^4-2048R^3S^2r^5-1152R^2S^2r^6-240RS^2r^7-17S^2r^8+768R^3S^3r^3+2144R^2S^3r^4+712RS^3r^5+56S^3r^6-64R^2S^4r^2+20RS^4r^3+117S^4r^4-152RS^5r-188S^5r^2+41S^6)(4Rr+r^2-2S)^2FJ^2+r^4(589824R^8r^8+1179648R^7r^9+1032192R^6r^{10}+516096R^5r^{11}+161280R^4r^{12}+32256R^3r^{13}+4032R^2r^{14}+288Rr^{15}+9r^{16}-1179648R^7Sr^7-2064384R^6Sr^8-1548288R^5Sr^9-645120R^4Sr^{10}-161280R^3Sr^{11}-24192R^2Sr^{12}-2016RSr^{13}-72Sr^{14}+491520R^6S^2r^6+774144R^5S^2r^7+506880R^4S^2r^8+176640R^3S^2r^9+34560R^2S^2r^{10}+3600RS^2r^{11}+156S^2r^{12}+380928R^5S^3r^5+374784R^4S^3r^6+136704R^3S^3r^7+21504R^2S^3r^8+1104RS^3r^9-24S^3r^{10}-307712R^4S^4r^4-226304R^3S^4r^5-55488R^2S^4r^6-4544RS^4r^7-2S^4r^8+1024R^3S^5r^3-5760R^2S^5r^4-1344RS^5r^5+40S^5r^6+39936R^2S^6r^2+4176RS^6r^3-2100S^6r^4-5744RS^7r+3064S^7r^2-671S^8)=0\)

9.  \(16(4Rr+r^2+2S)^2(4Rr+r^2-2S)^2LJ^4+(-2048R^6r^4+14336R^5r^5+19712R^4r^6+10112R^3r^7+2552R^2r^8+320Rr^9+16r^10+1024R^4S^2r^2-8704R^3S^2r^3-6848R^2S^2r^4-1728RS^2r^5-144S^2r^6-128R^2S^4+1280RS^4r+64S^4r^2)LJ^2+(16R^4r^2-120R^3r^3-95R^2r^4-24Rr^5-2r^6-16R^3Sr+92R^2Sr^2+40RSr^3+4Sr^4+4R^2S^2+8RS^2r+10S^2r^2-12S^3)(16R^4r^2-120R^3r^3-95R^2r^4-24Rr^5-2r^6+16R^3Sr-92R^2Sr^2-40RSr^3-4Sr^4+4R^2S^2+8RS^2r+10S^2r^2+12S^3)=0\)



若做\(R,r,p\)代换得到：

1.  \((2p+4R+r)^2(-2p+4R+r)^2OJ^4+(-512R^6-512R^5r+256R^4p^2-192R^4r^2-32R^3r^3-32R^2p^4-176R^2p^2r^2-2R^2r^4+32Rp^4r-72Rp^2r^3+16p^4r^2-8p^2r^4)OJ^2+(16R^4-16R^3p+8R^3r+4R^2p^2+12R^2pr+R^2r^2-12Rp^2r+12Rpr^2+2p^3r-4p^2r^2+2pr^3)(16R^4+16R^3p+8R^3r+4R^2p^2-12R^2pr+R^2r^2-12Rp^2r-12Rpr^2-2p^3r-4p^2r^2-2pr^3)=0\)

2.  \(81(2p+4R+r)^2(-2p+4R+r)^2GJ^4+(73728R^5r-4608R^4p^2+92160R^4r^2-48384R^3p^2r+46080R^3r^3+2304R^2p^4-37152R^2p^2r^2+11520R^2r^4+7488Rp^4r-9792Rp^2r^3+1440Rr^5-288p^6+1080p^4r^2-864p^2r^4+72r^6)GJ^2+(16(64R^3r-4R^2p^2-64R^2pr+48R^2r^2+4Rp^3+8Rp^2r-32Rpr^2+12Rr^3-p^4+4p^3r-4pr^3+r^4))(64R^3r-4R^2p^2+64R^2pr+48R^2r^2-4Rp^3+8Rp^2r+32Rpr^2+12Rr^3-p^4-4p^3r+4pr^3+r^4)=0\)

3.  \((2p+4R+r)^2(-2p+4R+r)^2HJ^4+(-2048R^6-2048R^5r+1536R^4p^2-768R^4r^2+1024R^3p^2r-128R^3r^3-384R^2p^4+352R^2p^2r^2-8R^2r^4-128Rp^4r+80Rp^2r^3+32p^6-56p^4r^2+8p^2r^4)HJ^2+(16(16R^4-16R^3p+8R^3r-12R^2pr+R^2r^2+4Rp^3+6Rp^2r-6Rpr^2-p^4-p^3r+3p^2r^2-pr^3))(16R^4+16R^3p+8R^3r+12R^2pr+R^2r^2-4Rp^3+6Rp^2r+6Rpr^2-p^4+p^3r+3p^2r^2+pr^3)=0\)

4.  \((2p+4R+r)^2(-2p+4R+r)^2IJ^4-2r^2(16R^2+8Rr+4p^2+r^2)(16R^2+8Rr-3p^2+r^2)IJ^2+r^4(16R^2+8Rr-3p^2+r^2)^2=0\)

8.  \(9(16R^2r^2-8Rp^2r+8Rr^3+p^4-14p^2r^2+r^4)(4R-2p+r)^4FJ^4+6r^2(3072R^5r-768R^4p^2-3072R^4pr+3840R^4r^2+768R^3p^3-2048R^3p^2r-3072R^3pr^2+1920R^3r^3-64R^2p^4+2144R^2p^3r-1152R^2p^2r^2-1152R^2pr^3+480R^2r^4-152Rp^5+20Rp^4r+712Rp^3r^2-240Rp^2r^3-192Rpr^4+60Rr^5+41p^6-188p^5r+117p^4r^2+56p^3r^3-17p^2r^4-12pr^5+3r^6)(4R-2p+r)^2FJ^2+r^4(589824R^8-1179648R^7p+1179648R^7r+491520R^6p^2-2064384R^6pr+1032192R^6r^2+380928R^5p^3+774144R^5p^2r-1548288R^5pr^2+516096R^5r^3-307712R^4p^4+374784R^4p^3r+506880R^4p^2r^2-645120R^4pr^3+161280R^4r^4+1024R^3p^5-226304R^3p^4r+136704R^3p^3r^2+176640R^3p^2r^3-161280R^3pr^4+32256R^3r^5+39936R^2p^6-5760R^2p^5r-55488R^2p^4r^2+21504R^2p^3r^3+34560R^2p^2r^4-24192R^2pr^5+4032R^2r^6-5744Rp^7+4176Rp^6r-1344Rp^5r^2-4544Rp^4r^3+1104Rp^3r^4+3600Rp^2r^5-2016Rpr^6+288Rr^7-671p^8+3064p^7r-2100p^6r^2+40p^5r^3-2p^4r^4-24p^3r^5+156p^2r^6-72pr^7+9r^8)=0\)

9.  \(16(2p+4R+r)^2(-2p+4R+r)^2LJ^4+(-2048R^6+14336R^5r+1024R^4p^2+19712R^4r^2-8704R^3p^2r+10112R^3r^3-128R^2p^4-6848R^2p^2r^2+2552R^2r^4+1280Rp^4r-1728Rp^2r^3+320Rr^5+64p^4r^2-144p^2r^4+16r^6)LJ^2+(16R^4-16R^3p-120R^3r+4R^2p^2+92R^2pr-95R^2r^2+8Rp^2r+40Rpr^2-24Rr^3-12p^3r+10p^2r^2+4pr^3-2r^4)(16R^4+16R^3p-120R^3r+4R^2p^2-92R^2pr-95R^2r^2+8Rp^2r-40Rpr^2-24Rr^3+12p^3r+10p^2r^2-4pr^3-2r^4)=0\)

数学星空

关于 Steiner椭圆焦点\(F_1,F_2\),有如下基本计算公式

设三角形的内切Steiner椭圆的长轴与短轴计算见 http://bbs.emath.ac.cn/forum.php ... 83&fromuid=1455

\(m=\frac{\sqrt{a^2+b^2+c^2+2\sqrt{a^4+b^4+c^4-a^2b^2-a^2c^2-b^2c^2}}}{6}\)

\(n=\frac{\sqrt{a^2+b^2+c^2-2\sqrt{a^4+b^4+c^4-a^2b^2-a^2c^2-b^2c^2}}}{6}\)

椭圆的中心为三角形的重心\(G\),且椭圆相切于各边的中点\(D,E,F\),设\(s=\sqrt{a^4-a^2b^2-a^2c^2+b^4-b^2c^2+c^4}\)

\(AF_1,AF_2\)满足下列方程(实根\(z\))：

\(-b^4c^4-81z^8-4(a^2-2b^2-2c^2)b^2c^2z^2+36(-a^2+2b^2+2c^2)z^6+6(2a^2b^2+2a^2c^2-2b^4-9b^2c^2-2c^4)z^4=0\)

\(AF_1=\frac{\sqrt{-a^2+2b^2+2c^2+s-\sqrt{2a^4-5a^2b^2-5a^2c^2+5b^4-2b^2c^2+5c^4-2a^2s+4b^2s+4c^2s}}}{3}\)

\(AF_2=\frac{\sqrt{-a^2+2b^2+2c^2+s+\sqrt{2a^4-5a^2b^2-5a^2c^2+5b^4-2b^2c^2+5c^4-2a^2s+4b^2s+4c^2s}}}{3}\)

\(BF_1,BF_2\)满足下列方程(实根\(z\))：

\(-c^4a^4-81z^8-4(-2a^2+b^2-2c^2)c^2a^2z^2+36(2a^2-b^2+2c^2)z^6+6(-2a^4+2a^2b^2-9a^2c^2+2b^2c^2-2c^4)z^4=0\)

\(BF_1=\frac{\sqrt{2a^2-b^2+2c^2+s-\sqrt{5a^4-5a^2b^2-2a^2c^2+2b^4-5b^2c^2+5c^4+4a^2s-2b^2s+4c^2s}}}{3}\)

\(BF_2=\frac{\sqrt{2a^2-b^2+2c^2+s+\sqrt{5a^4-5a^2b^2-2a^2c^2+2b^4-5b^2c^2+5c^4+4a^2s-2b^2s+4c^2s}}}{3}\)

\(CF_1,CF_2\)满足下列方程(实根\(z\))：

\(-a^4b^4-81z^8-4(-2a^2-2b^2+c^2)a^2b^2z^2+36(2a^2+2b^2-c^2)z^6+6(-2a^4-9a^2b^2+2a^2c^2-2b^4+2b^2c^2)z^4=0\)

\(CF_2=\frac{\sqrt{2a^2+2b^2-c^2+s-\sqrt{5a^4-2a^2b^2-5a^2c^2+5b^4-5b^2c^2+2c^4+4a^2s+4b^2s-2c^2s}}}{3}\)

\(CF_1=\frac{\sqrt{2a^2+2b^2-c^2+s+\sqrt{5a^4-2a^2b^2-5a^2c^2+5b^4-5b^2c^2+2c^4+4a^2s+4b^2s-2c^2s}}}{3}\)

数学星空

若设\(A(x,y),B(0,0),C(a,0)\),我们用解析法求解焦点坐标\(F_1(x_1,y_1),F_2(x_2,y_2)\)

则我们有结果：

为了表达方便，我们选取如下参数:

\(S =\sqrt{-a^4+2a^2b^2+2a^2c^2-b^4+2b^2c^2-c^4}\)

\(s =\sqrt{a^4-a^2b^2-a^2c^2+b^4-b^2c^2+c^4}\)

\(s_1 =\sqrt{5a^4-5a^2b^2-2a^2c^2+2b^4-5b^2c^2+5c^4+4a^2s-2b^2s+4c^2s}\)

\(s_2 =\sqrt{2a^4-5a^2b^2-5a^2c^2+5b^4-2b^2c^2+5c^4-2a^2s+4b^2s+4c^2s}\)

\(s_3 =\sqrt{-16a^4+28a^2b^2+25a^2c^2-16b^4+25b^2c^2-19c^4-2a^2s+6a^2s_1-6a^2s_2-2b^2s-6b^2s_1+6b^2s_2+28c^2s-18c^2s_1-18c^2s_2+2s_1s_2}\)

\(s_4 =\sqrt{-16a^4+28a^2b^2+25a^2c^2-16b^4+25b^2c^2-19c^4-2a^2s-6a^2s_1+6a^2s_2-2b^2s+6b^2s_1-6b^2s_2+28c^2s+18c^2s_1+18c^2s_2+2s_1s_2}\)

则

\(x_1 = \frac{3a^4-6a^2b^2+12a^2c^2+3b^4-12b^2c^2+9c^4-a^2s_1+a^2s_2+b^2s_1-b^2s_2-c^2s_1+c^2s_2+Ss_3}{36ac^2}\)

\(y_1= \frac{3Sa^2-3Sb^2+9Sc^2-a^2s_3+b^2s_3-c^2s_3-Ss_1+Ss_2}{36ac^2}\)

\(x_2 = \frac{3a^4-6a^2b^2+12a^2c^2+3b^4-12b^2c^2+9c^4+a^2s_1-a^2s_2-b^2s_1+b^2s_2+c^2s_1-c^2s_2+Ss_4}{36ac^2}\)

\(y_2 = \frac{3Sa^2-3Sb^2+9Sc^2-a^2s_4+b^2s_4-c^2s_4+Ss_1-Ss_2}{36ac^2}\)

在坐标系中椭圆方程为：\(\sqrt{(x-x_1)^2+(y-y_1)^2}+\sqrt{(x-x_2)^2+(y-y_2)^2}=2m\)

数学星空

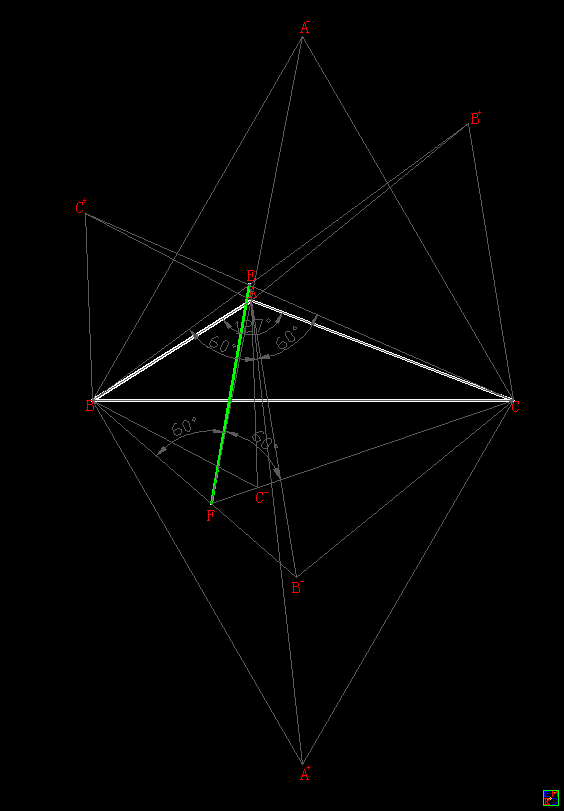
关于正负等角中心\(E,F\),我们可以得到如下基本公式：

设\(s=\sqrt{a^4-a^2b^2-a^2c^2+b^4-b^2c^2+c^4}\),   \(s_0=\sqrt{3(-a^4+2a^2b^2+2a^2c^2-b^4+2b^2c^2-c^4)}\)

\(AE,AF\)满足下列方程：（\(t_1\)实根）

\((9a^4-9a^2b^2-9a^2c^2+9b^4-9b^2c^2+9c^4)t_1^4+(3a^6-12a^4b^2-12a^4c^2+15a^2b^4+9a^2b^2c^2+15a^2c^4-6b^6-3b^4c^2-3b^2c^4-6c^6)t_1^2+(a^2-b^2-bc-c^2)^2(a^2-b^2+bc-c^2)^2=0\)

\(AE=\frac{\sqrt{-a^6+4a^4b^2+4a^4c^2-5a^2b^4-3a^2b^2c^2-5a^2c^4+2b^6+b^4c^2+b^2c^4+2c^6-a^4s_0+a^2b^2s_0+a^2c^2s_0-b^2c^2s_0}}{\sqrt{6}s}\)

\(AF=\frac{\sqrt{-a^6+4a^4b^2+4a^4c^2-5a^2b^4-3a^2b^2c^2-5a^2c^4+2b^6+b^4c^2+b^2c^4+2c^6+a^4s_0-a^2b^2s_0-a^2c^2s_0+b^2c^2s_0}}{\sqrt{6}s}\)


\(BE,BF\)满足下列方程：（\(t_2\)实根）

\((9a^4-9a^2b^2-9a^2c^2+9b^4-9b^2c^2+9c^4)t_2^4+(-6a^6+15a^4b^2-3a^4c^2-12a^2b^4+9a^2b^2c^2-3a^2c^4+3b^6-12b^4c^2+15b^2c^4-6c^6)t_2^2+(a^2-ac-b^2+c^2)^2(a^2+ac-b^2+c^2)^2=0\)

\(BE=\frac{\sqrt{12a^6-30a^4b^2+6a^4c^2+24a^2b^4-18a^2b^2c^2+6a^2c^4-6b^6+24b^4c^2-30b^2c^4+12c^6+6a^2b^2s_0-6a^2c^2s_0-6b^4s_0+6b^2c^2s_0}}{6s}\)

\(BF=\frac{\sqrt{12a^6-30a^4b^2+6a^4c^2+24a^2b^4-18a^2b^2c^2+6a^2c^4-6b^6+24b^4c^2-30b^2c^4+12c^6-6a^2b^2s_0+6a^2c^2s_0+6b^4s_0-6b^2c^2s_0}}{6s}\)

\(CE,CF\)满足下列方程：（\(t_3\)实根）

\((9a^4-9a^2b^2-9a^2c^2+9b^4-9b^2c^2+9c^4)t_3^4+(-6a^6-3a^4b^2+15a^4c^2-3a^2b^4+9a^2b^2c^2-12a^2c^4-6b^6+15b^4c^2-12b^2c^4+3c^6)t_3^2+(a^2+ab+b^2-c^2)^2(a^2-ab+b^2-c^2)^2=0\)

\(CE=\frac{\sqrt{2a^6+a^4b^2-5a^4c^2+a^2b^4-3a^2b^2c^2+4a^2c^4+2b^6-5b^4c^2+4b^2c^4-c^6-a^2b^2s_0+a^2c^2s_0+b^2c^2s_0-c^4s_0}}{\sqrt{6}s}\)

\(CF=\frac{\sqrt{2a^6+a^4b^2-5a^4c^2+a^2b^4-3a^2b^2c^2+4a^2c^4+2b^6-5b^4c^2+4b^2c^4-c^6+a^2b^2s_0-a^2c^2s_0-b^2c^2s_0+c^4s_0}}{\sqrt{6}s}\)



--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
为了不引起混淆，由于前面已将费马点定义为\(F\),故重新定义正负等角中心为(\E_1,E_2\)，注此时定义的\(E_1\)可理解为广义的费马点 \(F\)

即重新定义后的参数如下：

关于正负等角中心\(E_1,E_2\),我们可以得到如下基本公式：

设\(s=\sqrt{a^4-a^2b^2-a^2c^2+b^4-b^2c^2+c^4}\),   \(s_0=\sqrt{3(-a^4+2a^2b^2+2a^2c^2-b^4+2b^2c^2-c^4)}\)

\(AE_1,AE_2\)满足下列方程：（\(t_1\)实根）

\((9a^4-9a^2b^2-9a^2c^2+9b^4-9b^2c^2+9c^4)t_1^4+(3a^6-12a^4b^2-12a^4c^2+15a^2b^4+9a^2b^2c^2+15a^2c^4-6b^6-3b^4c^2-3b^2c^4-6c^6)t_1^2+(a^2-b^2-bc-c^2)^2(a^2-b^2+bc-c^2)^2=0\)

\(AE_1=\frac{\sqrt{-a^6+4a^4b^2+4a^4c^2-5a^2b^4-3a^2b^2c^2-5a^2c^4+2b^6+b^4c^2+b^2c^4+2c^6-a^4s_0+a^2b^2s_0+a^2c^2s_0-b^2c^2s_0}}{\sqrt{6}s}\)

\(AE_2=\frac{\sqrt{-a^6+4a^4b^2+4a^4c^2-5a^2b^4-3a^2b^2c^2-5a^2c^4+2b^6+b^4c^2+b^2c^4+2c^6+a^4s_0-a^2b^2s_0-a^2c^2s_0+b^2c^2s_0}}{\sqrt{6}s}\)


\(BE_1,BE_2\)满足下列方程：（\(t_2\)实根）

\((9a^4-9a^2b^2-9a^2c^2+9b^4-9b^2c^2+9c^4)t_2^4+(-6a^6+15a^4b^2-3a^4c^2-12a^2b^4+9a^2b^2c^2-3a^2c^4+3b^6-12b^4c^2+15b^2c^4-6c^6)t_2^2+(a^2-ac-b^2+c^2)^2(a^2+ac-b^2+c^2)^2=0\)

\(BE_1=\frac{\sqrt{12a^6-30a^4b^2+6a^4c^2+24a^2b^4-18a^2b^2c^2+6a^2c^4-6b^6+24b^4c^2-30b^2c^4+12c^6+6a^2b^2s_0-6a^2c^2s_0-6b^4s_0+6b^2c^2s_0}}{6s}\)

\(BE_2=\frac{\sqrt{12a^6-30a^4b^2+6a^4c^2+24a^2b^4-18a^2b^2c^2+6a^2c^4-6b^6+24b^4c^2-30b^2c^4+12c^6-6a^2b^2s_0+6a^2c^2s_0+6b^4s_0-6b^2c^2s_0}}{6s}\)

\(CE_1,CE_2\)满足下列方程：（\(t_3\)实根）

\((9a^4-9a^2b^2-9a^2c^2+9b^4-9b^2c^2+9c^4)t_3^4+(-6a^6-3a^4b^2+15a^4c^2-3a^2b^4+9a^2b^2c^2-12a^2c^4-6b^6+15b^4c^2-12b^2c^4+3c^6)t_3^2+(a^2+ab+b^2-c^2)^2(a^2-ab+b^2-c^2)^2=0\)

\(CE_1=\frac{\sqrt{2a^6+a^4b^2-5a^4c^2+a^2b^4-3a^2b^2c^2+4a^2c^4+2b^6-5b^4c^2+4b^2c^4-c^6-a^2b^2s_0+a^2c^2s_0+b^2c^2s_0-c^4s_0}}{\sqrt{6}s}\)

\(CE_2=\frac{\sqrt{2a^6+a^4b^2-5a^4c^2+a^2b^4-3a^2b^2c^2+4a^2c^4+2b^6-5b^4c^2+4b^2c^4-c^6+a^2b^2s_0-a^2c^2s_0-b^2c^2s_0+c^4s_0}}{\sqrt{6}s}\)

数学星空

关于等力点\(S,T\)的基本计算公式：

\(s=\sqrt{a^4-a^2b^2-a^2c^2+b^4-b^2c^2+c^4}\)

\(S=\sqrt{2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4}\)

\(K_1=\frac{\sqrt{(a^2+b^2+c^2+\sqrt{3}S)}abc}{\sqrt{2}s}=\frac{\sqrt{2}abc}{\sqrt{a^2+b^2+c^2-\sqrt{3}S}}\)

\(K_2=\frac{\sqrt{(a^2+b^2+c^2-\sqrt{3}S)}abc}{\sqrt{2}s}=\frac{\sqrt{2}abc}{\sqrt{a^2+b^2+c^2+\sqrt{3}S}}\)


则

\(AS=\frac{K_1}{a},BS=\frac{K_1}{b},CS=\frac{K_1}{c}\)

\(AT=\frac{K_2}{a},BT=\frac{K_2}{b},CT=\frac{K_2}{c}\)

数学星空

对于正负Brocard点\(X,Y\)有如下基本公式：设\(AX=x,BX=y,CX=z\)

\((a^2b^2+a^2c^2+b^2c^2)x^2-c^4b^2=0\)

\((a^2b^2+a^2c^2+b^2c^2)y^2-c^2a^4=0\)

\((a^2b^2+a^2c^2+b^2c^2)z^2-b^4a^2=0\)

\((4a^2b^2+4a^2c^2+4b^2c^2)\sin(\varphi)^2+a^4-2a^2b^2-2a^2c^2+b^4-2b^2c^2+c^4=0\)

容易得到

\(\sin(\varphi) =\frac{\sqrt{-a^4+2a^2b^2+2a^2c^2-b^4+2b^2c^2-c^4}}{2\sqrt{a^2b^2+a^2c^2+b^2c^2}}\)

\(AX=\frac{c^2b}{\sqrt{a^2b^2+a^2c^2+b^2c^2}}\)

\(BX=\frac{ca^2}{\sqrt{a^2b^2+a^2c^2+b^2c^2}}\)

\(CX=\frac{b^2a}{\sqrt{a^2b^2+a^2c^2+b^2c^2}}\)



若设\(AY=x,BY=y,CY=z\),则

\((a^2b^2+a^2c^2+b^2c^2)x^2-c^2b^4=0\)

\((a^2b^2+a^2c^2+b^2c^2)y^2-c^4a^2=0\)

\((a^2b^2+a^2c^2+b^2c^2)z^2-b^2a^4=0\)

\((4a^2b^2+4a^2c^2+4b^2c^2)\sin(\varphi)^2+a^4-2a^2b^2-2a^2c^2+b^4-2b^2c^2+c^4=0\)

容易得到

\(\sin(\varphi) =\frac{\sqrt{-a^4+2a^2b^2+2a^2c^2-b^4+2b^2c^2-c^4}}{2\sqrt{a^2b^2+a^2c^2+b^2c^2}}\)

\(AY=\frac{b^2c}{\sqrt{a^2b^2+a^2c^2+b^2c^2}}\)

\(BY=\frac{ac^2}{\sqrt{a^2b^2+a^2c^2+b^2c^2}}\)

\(CY=\frac{a^2b}{\sqrt{a^2b^2+a^2c^2+b^2c^2}}\)

并且有\(\frac{1}{\sin(\varphi)^2}=\frac{1}{\sin(A)^2}+\frac{1}{\sin(B)^2}+\frac{1}{\sin(C)^2}\)

数学星空

关于11#提到的内点\(PA=x,PB=y,PC=z\)的一个很简洁表达式的注记

\( (-a^2+y^2+z^2)^2x^2+(-b^2+x^2+z^2)^2y^2+(-c^2+x^2+y^2)^2z^2-(-a^2+y^2+z^2)(-b^2+x^2+z^2)(-c^2+x^2+y^2)-4x^2y^2z^2＝0\)

\(＝(2yz\cos(\alpha))^2x^2+(2xz\cos(\beta))^2y^2+(2xy\cos(\gamma))^2z^2-2yz\cos(\alpha)2xz\cos(\beta)2xy\cos(\gamma)-4x^2y^2z^2\)

\(=4x^2y^2z^2((\cos(\alpha))^2+(\cos(\beta))^2+(\cos(\gamma))^2-2\cos(\alpha)\cos(\beta)\cos(\gamma)-1)\)

即本质上就是\( \alpha+\beta+\gamma=2\pi\) 条件下

\((\cos(\alpha))^2+(\cos(\beta))^2+(\cos(\gamma))^2-2\cos(\alpha)\cos(\beta)\cos(\gamma)-1\)

\(＝(\cos(\alpha))^2+(\cos(\beta))^2+(\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta))^2-2\cos(\alpha)\cos(\beta)(\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta))-1\)

\(=(\cos(\alpha))^2+(\cos(\beta))^2+(\cos(\alpha))^2(\cos(\beta))^2+(1-(\cos(\alpha))^2)(1-(\cos(\beta))^2)-2(\cos(\alpha))^2(\cos(\beta))^2-1\)

\(=0\)

数学星空

关于正负Brocard点\(X,Y\)的心距公式：

1.  (a^2+b^2+c^2)*(a+b+c)^2*(-c+a-b)^2*(-c+a+b)^2*(c+a-b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*OX^4+(a+b+c)*(-c+a-b)*(-c+a+b)*(c+a-b)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^10*b^2-3*a^8*b^4-a^8*b^2*c^2-a^8*c^4+3*a^6*b^6+a^6*b^4*c^2+4*a^6*b^2*c^4+3*a^6*c^6-a^4*b^8+4*a^4*b^6*c^2-3*a^4*b^4*c^4+a^4*b^2*c^6-3*a^4*c^8-a^2*b^8*c^2+a^2*b^6*c^4+4*a^2*b^4*c^6-a^2*b^2*c^8+a^2*c^10+b^10*c^2-3*b^8*c^4+3*b^6*c^6-b^4*c^8)*OX^2+a^2*b^2*c^2*(a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)*(a^10*b^2-3*a^8*b^4-2*a^8*b^2*c^2-a^8*c^4+3*a^6*b^6+a^6*b^4*c^2+4*a^6*b^2*c^4+3*a^6*c^6-a^4*b^8+4*a^4*b^6*c^2+a^4*b^2*c^6-3*a^4*c^8-2*a^2*b^8*c^2+a^2*b^6*c^4+4*a^2*b^4*c^6-2*a^2*b^2*c^8+a^2*c^10+b^10*c^2-3*b^8*c^4+3*b^6*c^6-b^4*c^8)=0

2.  (81*(a^2+b^2+c^2))*(a^2*b^2+a^2*c^2+b^2*c^2)^2*GX^4+(9*(a^2*b^2+a^2*c^2+b^2*c^2))*(5*a^6*b^2-a^6*c^2-8*a^4*b^4-5*a^4*b^2*c^2-8*a^4*c^4-a^2*b^6-5*a^2*b^4*c^2-5*a^2*b^2*c^4+5*a^2*c^6+5*b^6*c^2-8*b^4*c^4-b^2*c^6)*GX^2+(a^4*b^2-2*a^4*c^2-2*a^2*b^4+3*a^2*b^2*c^2+a^2*c^4+b^4*c^2-2*b^2*c^4)*(4*a^6*b^2+a^6*c^2-7*a^4*b^4-7*a^4*b^2*c^2-7*a^4*c^4+a^2*b^6-7*a^2*b^4*c^2-7*a^2*b^2*c^4+4*a^2*c^6+4*b^6*c^2-7*b^4*c^4+b^2*c^6)=0

3.  (a^2+b^2+c^2)*(-c+a+b)^2*(a+b+c)^2*(c+a-b)^2*(-c+a-b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*HX^4+(-c+a+b)*(a+b+c)*(c+a-b)*(-c+a-b)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^2+b^2+c^2)*(a^8*b^2+a^8*c^2-a^6*b^4-3*a^6*b^2*c^2-a^6*c^4-a^4*b^6+4*a^4*b^4*c^2+4*a^4*b^2*c^4-a^4*c^6+a^2*b^8-3*a^2*b^6*c^2+4*a^2*b^4*c^4-3*a^2*b^2*c^6+a^2*c^8+b^8*c^2-b^6*c^4-b^4*c^6+b^2*c^8)*HX^2+(a^2+b^2+c^2)*(a^8*b^2-2*a^6*b^4-a^6*b^2*c^2+a^6*c^4+a^4*b^6+a^4*b^4*c^2+a^4*b^2*c^4-2*a^4*c^6-a^2*b^6*c^2+a^2*b^4*c^4-a^2*b^2*c^6+a^2*c^8+b^8*c^2-2*b^6*c^4+b^4*c^6)*(a^8*c^2+a^6*b^4-2*a^6*b^2*c^2-2*a^6*c^4-2*a^4*b^6+3*a^4*b^4*c^2+3*a^4*b^2*c^4+a^4*c^6+a^2*b^8-2*a^2*b^6*c^2+3*a^2*b^4*c^4-2*a^2*b^2*c^6+b^6*c^4-2*b^4*c^6+b^2*c^8)=0

4.  (a^2+b^2+c^2)*(a+b+c)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*IX^4+(a+b+c)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^7*b^2-2*a^6*b*c^2+a^6*c^3-2*a^5*b^4+2*a^5*b^3*c-2*a^5*b^2*c^2+2*a^5*b*c^3-2*a^4*b^4*c-a^4*b^3*c^2-2*a^4*b^2*c^3-2*a^4*b*c^4-2*a^4*c^5+a^3*b^6+2*a^3*b^5*c-2*a^3*b^4*c^2+6*a^3*b^3*c^3-a^3*b^2*c^4+2*a^3*b*c^5-2*a^2*b^6*c-2*a^2*b^5*c^2-a^2*b^4*c^3-2*a^2*b^3*c^4-2*a^2*b^2*c^5+a^2*c^7+2*a*b^5*c^3-2*a*b^4*c^4+2*a*b^3*c^5-2*a*b^2*c^6+b^7*c^2-2*b^5*c^4+b^3*c^6)*IX^2-a*b*c*(a^3*c-a^2*b^2-a^2*c^2+a*b^3-b^2*c^2+b*c^3)*(a^7*b^2-a^6*b*c^2+a^6*c^3-2*a^5*b^4+a^5*b^3*c-2*a^5*b^2*c^2+a^5*b*c^3-a^4*b^4*c-2*a^4*b^2*c^3-a^4*b*c^4-2*a^4*c^5+a^3*b^6+a^3*b^5*c-2*a^3*b^4*c^2+3*a^3*b^3*c^3+a^3*b*c^5-a^2*b^6*c-2*a^2*b^5*c^2-2*a^2*b^3*c^4-2*a^2*b^2*c^5+a^2*c^7+a*b^5*c^3-a*b^4*c^4+a*b^3*c^5-a*b^2*c^6+b^7*c^2-2*b^5*c^4+b^3*c^6)=0

5.  (a^2+b^2+c^2)*(-c+a-b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*O1X^4+(-c+a-b)*(a^7*b^2+2*a^6*b*c^2-a^6*c^3-2*a^5*b^4+2*a^5*b^3*c-2*a^5*b^2*c^2+2*a^5*b*c^3+2*a^4*b^4*c+a^4*b^3*c^2+2*a^4*b^2*c^3+2*a^4*b*c^4+2*a^4*c^5+a^3*b^6+2*a^3*b^5*c-2*a^3*b^4*c^2+6*a^3*b^3*c^3-a^3*b^2*c^4+2*a^3*b*c^5+2*a^2*b^6*c+2*a^2*b^5*c^2+a^2*b^4*c^3+2*a^2*b^3*c^4+2*a^2*b^2*c^5-a^2*c^7+2*a*b^5*c^3-2*a*b^4*c^4+2*a*b^3*c^5-2*a*b^2*c^6-b^7*c^2+2*b^5*c^4-b^3*c^6)*(a^2*b^2+a^2*c^2+b^2*c^2)*O1X^2+a*b*c*(a^7*b^2+a^6*b*c^2-a^6*c^3-2*a^5*b^4+a^5*b^3*c-2*a^5*b^2*c^2+a^5*b*c^3+a^4*b^4*c+2*a^4*b^2*c^3+a^4*b*c^4+2*a^4*c^5+a^3*b^6+a^3*b^5*c-2*a^3*b^4*c^2+3*a^3*b^3*c^3+a^3*b*c^5+a^2*b^6*c+2*a^2*b^5*c^2+2*a^2*b^3*c^4+2*a^2*b^2*c^5-a^2*c^7+a*b^5*c^3-a*b^4*c^4+a*b^3*c^5-a*b^2*c^6-b^7*c^2+2*b^5*c^4-b^3*c^6)*(a^3*c+a^2*b^2+a^2*c^2+a*b^3+b^2*c^2-b*c^3)=0

6.  (a^2+b^2+c^2)*(c+a-b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*O2X^4+(c+a-b)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^7*b^2+2*a^6*b*c^2+a^6*c^3-2*a^5*b^4-2*a^5*b^3*c-2*a^5*b^2*c^2-2*a^5*b*c^3-2*a^4*b^4*c+a^4*b^3*c^2-2*a^4*b^2*c^3+2*a^4*b*c^4-2*a^4*c^5+a^3*b^6-2*a^3*b^5*c-2*a^3*b^4*c^2-6*a^3*b^3*c^3-a^3*b^2*c^4-2*a^3*b*c^5-2*a^2*b^6*c+2*a^2*b^5*c^2-a^2*b^4*c^3+2*a^2*b^3*c^4-2*a^2*b^2*c^5+a^2*c^7-2*a*b^5*c^3-2*a*b^4*c^4-2*a*b^3*c^5-2*a*b^2*c^6-b^7*c^2+2*b^5*c^4-b^3*c^6)*O2X^2+a*b*c*(a^3*c-a^2*b^2-a^2*c^2-a*b^3-b^2*c^2-b*c^3)*(a^7*b^2+a^6*b*c^2+a^6*c^3-2*a^5*b^4-a^5*b^3*c-2*a^5*b^2*c^2-a^5*b*c^3-a^4*b^4*c-2*a^4*b^2*c^3+a^4*b*c^4-2*a^4*c^5+a^3*b^6-a^3*b^5*c-2*a^3*b^4*c^2-3*a^3*b^3*c^3-a^3*b*c^5-a^2*b^6*c+2*a^2*b^5*c^2+2*a^2*b^3*c^4-2*a^2*b^2*c^5+a^2*c^7-a*b^5*c^3-a*b^4*c^4-a*b^3*c^5-a*b^2*c^6-b^7*c^2+2*b^5*c^4-b^3*c^6)=0

7.  (a^2+b^2+c^2)*(-c+a+b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*O3X^4+(-c+a+b)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^7*b^2-2*a^6*b*c^2-a^6*c^3-2*a^5*b^4-2*a^5*b^3*c-2*a^5*b^2*c^2-2*a^5*b*c^3+2*a^4*b^4*c-a^4*b^3*c^2+2*a^4*b^2*c^3-2*a^4*b*c^4+2*a^4*c^5+a^3*b^6-2*a^3*b^5*c-2*a^3*b^4*c^2-6*a^3*b^3*c^3-a^3*b^2*c^4-2*a^3*b*c^5+2*a^2*b^6*c-2*a^2*b^5*c^2+a^2*b^4*c^3-2*a^2*b^3*c^4+2*a^2*b^2*c^5-a^2*c^7-2*a*b^5*c^3-2*a*b^4*c^4-2*a*b^3*c^5-2*a*b^2*c^6+b^7*c^2-2*b^5*c^4+b^3*c^6)*O3X^2-a*b*c*(a^3*c+a^2*b^2+a^2*c^2-a*b^3+b^2*c^2+b*c^3)*(a^7*b^2-a^6*b*c^2-a^6*c^3-2*a^5*b^4-a^5*b^3*c-2*a^5*b^2*c^2-a^5*b*c^3+a^4*b^4*c+2*a^4*b^2*c^3-a^4*b*c^4+2*a^4*c^5+a^3*b^6-a^3*b^5*c-2*a^3*b^4*c^2-3*a^3*b^3*c^3-a^3*b*c^5+a^2*b^6*c-2*a^2*b^5*c^2-2*a^2*b^3*c^4+2*a^2*b^2*c^5-a^2*c^7-a*b^5*c^3-a*b^4*c^4-a*b^3*c^5-a*b^2*c^6+b^7*c^2-2*b^5*c^4+b^3*c^6)=0

8.  b^4*a^12+a^12*c^4+c^12*b^4+b^12*c^4+a^4*b^12+a^4*c^12-4*a^6*c^10+6*b^8*a^8-4*b^10*a^6-4*c^10*b^6+6*c^8*b^8-4*b^10*c^6-4*c^6*a^10-4*b^6*a^10+6*c^8*a^8+(9*(a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4))*(a^2*b^2+a^2*c^2+b^2*c^2)^2*FX^4-a^6*b^8*c^2-a^2*b^8*c^6-a^12*b^2*c^2-c^2*a^2*b^12-a^2*b^2*c^12-a^8*b^2*c^6-a^8*b^6*c^2-a^2*b^6*c^8-a^6*b^2*c^8+3*a^4*b^6*c^6+2*a^10*c^4*b^2+3*a^6*b^6*c^4-4*c^8*a^4*b^4+(3*(a^2*b^2+a^2*c^2+b^2*c^2))*(a^8*b^2-2*a^8*c^2-4*a^6*b^4-a^6*b^2*c^2+5*a^6*c^4+5*a^4*b^6+a^4*b^4*c^2+a^4*b^2*c^4-4*a^4*c^6-2*a^2*b^8-a^2*b^6*c^2+a^2*b^4*c^4-a^2*b^2*c^6+a^2*c^8+b^8*c^2-4*b^6*c^4+5*b^4*c^6-2*b^2*c^8)*FX^2-4*c^4*b^8*a^4+2*c^4*b^10*a^2+2*b^10*a^4*c^2+2*c^10*b^4*a^2+2*c^2*a^10*b^4+3*a^6*b^4*c^6-4*c^4*a^8*b^4+2*a^4*b^2*c^10=0

9.  (16*(a^2+b^2+c^2))*(a+b+c)^2*(-c+a-b)^2*(-c+a+b)^2*(c+a-b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*LX^4+(8*(c+a-b))*(-c+a+b)*(a+b+c)*(-c+a-b)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^10*b^2-3*a^8*b^4-3*a^8*b^2*c^2-a^8*c^4+3*a^6*b^6+2*a^6*b^4*c^2+5*a^6*b^2*c^4+3*a^6*c^6-a^4*b^8+5*a^4*b^6*c^2+6*a^4*b^4*c^4+2*a^4*b^2*c^6-3*a^4*c^8-3*a^2*b^8*c^2+2*a^2*b^6*c^4+5*a^2*b^4*c^6-3*a^2*b^2*c^8+a^2*c^10+b^10*c^2-3*b^8*c^4+3*b^6*c^6-b^4*c^8)*LX^2+(a^2*b^2+a^2*c^2+b^2*c^2)*(a^8*b^2-a^8*c^2-3*a^6*b^4+a^6*b^2*c^2+3*a^6*c^4+3*a^4*b^6-a^4*b^4*c^2-a^4*b^2*c^4-3*a^4*c^6-a^2*b^8+a^2*b^6*c^2-a^2*b^4*c^4+a^2*b^2*c^6+a^2*c^8+b^8*c^2-3*b^6*c^4+3*b^4*c^6-b^2*c^8)*(a^8-4*a^6*b^2-4*a^6*c^2+6*a^4*b^4+5*a^4*b^2*c^2+6*a^4*c^4-4*a^2*b^6+5*a^2*b^4*c^2+5*a^2*b^2*c^4-4*a^2*c^6+b^8-4*b^6*c^2+6*b^4*c^4-4*b^2*c^6+c^8)=0

10.  a^4*b^20+a^20*c^4+b^4*c^20+16*c^4*b^20+271*c^12*b^12+129*a^16*b^8-84*a^10*b^14+70*a^6*b^18-42*a^14*b^10-84*c^10*a^14+168*a^7*c^17+271*c^12*a^12+223*a^8*b^16-42*c^10*b^14-42*c^14*a^10-32*a^19*b^5+271*a^12*b^12-384*a^15*b^9-72*c^6*b^18+70*c^6*a^18-32*a^5*c^19+16*a^4*c^20-384*c^13*b^11-72*a^6*c^18-8*a^5*b^19-32*c^5*b^19+88*a^9*b^15-224*b^7*c^17+70*b^6*c^18+16*a^20*b^4+88*c^15*b^9+223*c^8*a^16+129*c^8*b^16+264*c^11*b^13+264*c^13*a^11+129*c^16*a^8+223*c^16*b^8-224*a^7*b^17+88*c^9*a^15-84*c^14*b^10-384*c^11*a^13+168*c^7*b^17+264*a^13*b^11+168*a^17*b^7-384*c^15*a^9-72*a^18*b^6-224*c^7*a^17-8*c^5*a^19-384*c^9*b^15-384*a^11*b^13-8*b^5*c^19+(a^2+b^2+c^2)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*(5*a^4-4*a^3*b-4*a^3*c-2*a^2*b^2+4*a^2*b*c-2*a^2*c^2-4*a*b^3+4*a*b^2*c+4*a*b*c^2-4*a*c^3+5*b^4-4*b^3*c-2*b^2*c^2-4*b*c^3+5*c^4)^2*JX^4-8*c^3*a^10*b^11-352*c^6*a^11*b^7+192*c^10*a^9*b^5-872*c^3*a^11*b^10-1024*c^12*a^11*b+488*c^12*a^9*b^3+136*c^3*a^4*b^17-784*c^3*a^6*b^15+272*c^3*a^8*b^13+96*a*b^6*c^17-322*c^12*b^6*a^6-10*a^2*c^18*b^4-64*a*b^5*c^18+39*c^12*b^8*a^4+554*c^12*a^8*b^4+720*c^3*a^9*b^12+1560*c^5*a^7*b^12+128*a^5*c^18*b+280*c^9*a^11*b^4-1518*c^10*a^12*b^2+952*c^10*b^10*a^4+1560*c^12*b^7*a^5+152*c^12*a^7*b^5-656*c^10*a*b^13+64*c^10*b^9*a^5+122*c^10*b^6*a^8-64*c^5*a^18*b+952*c^10*a^10*b^4+648*c^10*b^8*a^6-288*c^10*b^7*a^7-1518*c^12*a^2*b^10-256*c^7*a^8*b^9+544*c^3*a^14*b^7+192*c^9*a^5*b^10+1056*c^10*a^13*b-352*c^13*a^2*b^9-48*a^2*b^5*c^17-8*c^11*a^3*b^10+432*c^12*a*b^11-8*c^10*a^11*b^3+152*c^5*a^12*b^7+8*c^3*a^2*b^19+8*a^6*c^17*b-1704*c^13*a^4*b^7-352*c^11*a^7*b^6+1390*c^10*a^2*b^12+8*c^6*a*b^17-8*a^20*b^2*c^2-288*c^7*a^7*b^10-432*c^13*a^9*b^2-352*c^9*a^13*b^2+208*c^7*a^15*b^2-296*c^5*a^15*b^4+96*c^6*a^3*b^15-1152*c^13*a^6*b^5-312*c^9*a^14*b-16*c^7*a^2*b^15-48*c^5*a^17*b^2-80*c^3*a^7*b^14-240*c^5*a^6*b^13+544*c^14*a^7*b^3-352*c^7*a^6*b^11+152*c^7*a^5*b^12+352*c^3*a^5*b^16+8*a^3*b^2*c^19-712*c^15*a^5*b^4-32*c*a^19*b^4+432*c*a^11*b^12-80*a^3*b^3*c^18-1704*c^7*a^13*b^4-16*a^4*b^3*c^17-872*c^10*a^3*b^11-240*c^6*a^13*b^5+752*c^11*a^6*b^7-16*c^4*a^3*b^17+242*c^4*b^6*a^14-1024*c^11*a*b^12+280*c^4*a^9*b^11-32*c^4*a*b^19+328*c^4*a^13*b^7+248*c^15*a^8*b+39*c^4*b^12*a^8+1430*c^4*b^14*a^6+99*c^4*b^16*a^4-296*c^4*a^5*b^15-10*a^18*b^2*c^4+268*c^6*a^2*b^16-784*c^6*a^15*b^3-1152*c^5*a^13*b^6-30*a^4*b^2*c^18-1152*c^6*a^5*b^13+952*c^4*b^10*a^10+554*c^4*b^8*a^12-712*c^4*a^15*b^5-30*c^4*a^2*b^18-1704*c^4*a^7*b^13+192*c^5*a^10*b^9-1376*c^4*a^11*b^9+136*c^4*a^17*b^3+1390*c^12*a^10*b^2+488*c^3*a^12*b^9-872*c^11*a^10*b^3-784*c^15*a^3*b^6+752*c^6*a^7*b^11+720*c^12*a^3*b^9-64*c^5*a^3*b^16+99*b^4*a^16*c^4+720*c^5*a^14*b^5-672*c^3*a^13*b^8-352*c^7*a^9*b^8+792*c^14*a^2*b^8+248*c^8*a*b^15-636*c^8*a^2*b^14+592*c^2*a^11*b^11-64*a^5*b^3*c^16+1430*c^6*a^14*b^4-672*c^13*a^8*b^3-16*c^15*a^7*b^2-248*c^9*a^6*b^9+720*c^14*a^5*b^5+488*c^9*a^3*b^12-296*c^15*a^4*b^5-312*c^14*a*b^9+64*c^9*a^10*b^5+752*c^7*a^11*b^6-752*c^15*a*b^8-240*c^6*a^16*b^2+504*c^5*a^11*b^8+122*c^6*a^10*b^8+432*c^11*a^12*b-80*c^14*a^3*b^7-712*c^5*a^4*b^15-352*c^9*a^8*b^7+8*c*a^17*b^6-248*c^6*a^9*b^9-80*b^3*a^18*c^3+1269*c^8*b^8*a^8+39*c^8*b^4*a^12+792*c^8*a^14*b^2-1776*c^8*a^11*b^5+122*c^8*b^10*a^6-288*c^7*a^10*b^7+592*c^11*a^2*b^11+280*c^11*a^4*b^9-240*c^13*a^5*b^6+376*c^7*a^16*b+328*c^13*a^7*b^4-80*c^7*a^14*b^3+1024*c^9*a*b^14+1560*c^7*a^12*b^5-528*c^7*a*b^16+328*c^7*a^4*b^13-1776*c^5*a^8*b^11-636*c^14*a^8*b^2-256*c^9*a^7*b^8-1776*c^11*a^5*b^8-672*c^8*a^3*b^13+272*c^8*a^13*b^3-752*c^8*a^15*b-1376*c^11*a^9*b^4+96*c^3*a^15*b^6-10*c^2*b^18*a^4-80*c^3*a^3*b^18+242*c^14*b^4*a^6+1430*c^14*b^6*a^4+1024*c^14*a^9*b+242*c^6*b^14*a^4+554*c^8*a^4*b^12+136*a^3*b^4*c^17+544*c^7*a^3*b^14-32*a^4*c^19*b-752*c*a^8*b^15+96*c^6*a^17*b-312*c*a^9*b^14+248*c*a^15*b^8+40*a^2*b^3*c^19+1024*c*a^14*b^9-256*c^8*a^9*b^7-352*c^8*a^7*b^9-30*c^2*a^18*b^4+40*c^2*a^3*b^19+8*c^2*a^19*b^3+648*c^6*a^8*b^10+720*c^5*a^5*b^14+272*c^13*a^3*b^8+64*c^5*a^9*b^10-656*c^13*a^10*b-322*c^6*a^12*b^6-352*c^2*a^9*b^13-16*c^2*a^15*b^7-1518*c^2*b^12*a^10+1390*c^2*b^10*a^12-636*c^2*a^14*b^8+268*c^2*a^16*b^6+376*c*a^7*b^16-322*c^6*a^6*b^12-528*c*a^16*b^7-1024*c*a^12*b^11-8*a^2*b^2*c^20-16*b^4*a^17*c^3+40*b^2*a^19*c^3+376*a*b^7*c^16+1056*c^13*a*b^10-432*c^2*a^13*b^9-48*c^2*a^5*b^17-240*c^2*b^16*a^6+792*c^2*b^14*a^8-8*c^2*a^2*b^20-432*c^9*a^2*b^13+208*c^2*a^7*b^15+128*c^5*a*b^18+268*c^16*a^6*b^2-240*c^16*a^2*b^6+99*c^16*a^4*b^4-248*c^9*a^9*b^6+352*a^3*b^5*c^16+128*c*a^18*b^5-64*c*a^5*b^18-64*b^5*a^16*c^3+648*c^8*b^6*a^10-656*c*a^13*b^10+96*c*a^6*b^17+504*c^11*a^8*b^5+96*c^15*a^6*b^3+720*c^9*a^12*b^3+504*c^8*a^5*b^11+208*c^15*a^2*b^7+1056*c*a^10*b^13+352*c^5*a^16*b^3-528*a^7*b*c^16-1376*c^9*a^4*b^11+592*c^11*a^11*b^2+(2*(a^2*b^2+a^2*c^2+b^2*c^2))*(a^2+b^2+c^2)*(12*a^14*b^2-3*a^14*c^2-12*a^13*b^3-12*a^13*b^2*c-20*a^13*b*c^2+40*a^13*c^3-63*a^12*b^4+40*a^12*b^3*c-7*a^12*b^2*c^2-28*a^12*b*c^3-99*a^12*c^4+88*a^11*b^5+52*a^11*b^4*c+80*a^11*b^3*c^2-32*a^11*b^2*c^3+200*a^11*b*c^4+52*a^11*c^5+33*a^10*b^6-228*a^10*b^5*c+3*a^10*b^4*c^2-224*a^10*b^3*c^3+a^10*b^2*c^4-92*a^10*b*c^5+22*a^10*c^6-8*a^9*b^7+40*a^9*b^6*c+12*a^9*b^5*c^2+376*a^9*b^4*c^3+28*a^9*b^3*c^4+20*a^9*b^2*c^5-232*a^9*b*c^6+96*a^9*c^7-158*a^8*b^8+240*a^8*b^7*c-78*a^8*b^6*c^2+44*a^8*b^5*c^3-563*a^8*b^4*c^4+184*a^8*b^3*c^5+207*a^8*b^2*c^6+40*a^8*b*c^7-158*a^8*c^8+96*a^7*b^9+40*a^7*b^8*c-176*a^7*b^7*c^2-256*a^7*b^6*c^3+464*a^7*b^5*c^4-64*a^7*b^4*c^5-16*a^7*b^3*c^6-176*a^7*b^2*c^7+240*a^7*b*c^8-8*a^7*c^9+22*a^6*b^10-232*a^6*b^9*c+207*a^6*b^8*c^2-16*a^6*b^7*c^3+228*a^6*b^6*c^4-240*a^6*b^5*c^5+228*a^6*b^4*c^6-256*a^6*b^3*c^7-78*a^6*b^2*c^8+40*a^6*b*c^9+33*a^6*c^10+52*a^5*b^11-92*a^5*b^10*c+20*a^5*b^9*c^2+184*a^5*b^8*c^3-64*a^5*b^7*c^4-240*a^5*b^6*c^5-240*a^5*b^5*c^6+464*a^5*b^4*c^7+44*a^5*b^3*c^8+12*a^5*b^2*c^9-228*a^5*b*c^10+88*a^5*c^11-99*a^4*b^12+200*a^4*b^11*c+a^4*b^10*c^2+28*a^4*b^9*c^3-563*a^4*b^8*c^4+464*a^4*b^7*c^5+228*a^4*b^6*c^6-64*a^4*b^5*c^7-563*a^4*b^4*c^8+376*a^4*b^3*c^9+3*a^4*b^2*c^10+52*a^4*b*c^11-63*a^4*c^12+40*a^3*b^13-28*a^3*b^12*c-32*a^3*b^11*c^2-224*a^3*b^10*c^3+376*a^3*b^9*c^4+44*a^3*b^8*c^5-256*a^3*b^7*c^6-16*a^3*b^6*c^7+184*a^3*b^5*c^8+28*a^3*b^4*c^9-224*a^3*b^3*c^10+80*a^3*b^2*c^11+40*a^3*b*c^12-12*a^3*c^13-3*a^2*b^14-20*a^2*b^13*c-7*a^2*b^12*c^2+80*a^2*b^11*c^3+3*a^2*b^10*c^4+12*a^2*b^9*c^5-78*a^2*b^8*c^6-176*a^2*b^7*c^7+207*a^2*b^6*c^8+20*a^2*b^5*c^9+a^2*b^4*c^10-32*a^2*b^3*c^11-7*a^2*b^2*c^12-12*a^2*b*c^13+12*a^2*c^14-12*a*b^13*c^2+40*a*b^12*c^3+52*a*b^11*c^4-228*a*b^10*c^5+40*a*b^9*c^6+240*a*b^8*c^7+40*a*b^7*c^8-232*a*b^6*c^9-92*a*b^5*c^10+200*a*b^4*c^11-28*a*b^3*c^12-20*a*b^2*c^13+12*b^14*c^2-12*b^13*c^3-63*b^12*c^4+88*b^11*c^5+33*b^10*c^6-8*b^9*c^7-158*b^8*c^8+96*b^7*c^9+22*b^6*c^10+52*b^5*c^11-99*b^4*c^12+40*b^3*c^13-3*b^2*c^14)*JX^2=0

数学星空

1. (a^2+b^2+c^2)*(a+b+c)^2*(-c+a+b)^2*(-c+a-b)^2*(c+a-b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*OY^4+(-c+a+b)*(c+a-b)*(a+b+c)*(-c+a-b)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^10*c^2-a^8*b^4-a^8*b^2*c^2-3*a^8*c^4+3*a^6*b^6+4*a^6*b^4*c^2+a^6*b^2*c^4+3*a^6*c^6-3*a^4*b^8+a^4*b^6*c^2-3*a^4*b^4*c^4+4*a^4*b^2*c^6-a^4*c^8+a^2*b^10-a^2*b^8*c^2+4*a^2*b^6*c^4+a^2*b^4*c^6-a^2*b^2*c^8-b^8*c^4+3*b^6*c^6-3*b^4*c^8+b^2*c^10)*OY^2+a^2*b^2*c^2*(a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)*(a^10*c^2-a^8*b^4-2*a^8*b^2*c^2-3*a^8*c^4+3*a^6*b^6+4*a^6*b^4*c^2+a^6*b^2*c^4+3*a^6*c^6-3*a^4*b^8+a^4*b^6*c^2+4*a^4*b^2*c^6-a^4*c^8+a^2*b^10-2*a^2*b^8*c^2+4*a^2*b^6*c^4+a^2*b^4*c^6-2*a^2*b^2*c^8-b^8*c^4+3*b^6*c^6-3*b^4*c^8+b^2*c^10)=0

2.  (81*(a^2+b^2+c^2))*(a^2*b^2+a^2*c^2+b^2*c^2)^2*GY^4-(9*(a^2*b^2+a^2*c^2+b^2*c^2))*(a^6*b^2-5*a^6*c^2+8*a^4*b^4+5*a^4*b^2*c^2+8*a^4*c^4-5*a^2*b^6+5*a^2*b^4*c^2+5*a^2*b^2*c^4+a^2*c^6+b^6*c^2+8*b^4*c^4-5*b^2*c^6)*GY^2-(2*a^4*b^2-a^4*c^2-a^2*b^4-3*a^2*b^2*c^2+2*a^2*c^4+2*b^4*c^2-b^2*c^4)*(a^6*b^2+4*a^6*c^2-7*a^4*b^4-7*a^4*b^2*c^2-7*a^4*c^4+4*a^2*b^6-7*a^2*b^4*c^2-7*a^2*b^2*c^4+a^2*c^6+b^6*c^2-7*b^4*c^4+4*b^2*c^6)=0

3.  (a^2+b^2+c^2)*(-c+a+b)^2*(c+a-b)^2*(a+b+c)^2*(-c+a-b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*HY^4+(-c+a+b)*(c+a-b)*(a+b+c)*(-c+a-b)*(a^2+b^2+c^2)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^8*b^2+a^8*c^2-a^6*b^4-3*a^6*b^2*c^2-a^6*c^4-a^4*b^6+4*a^4*b^4*c^2+4*a^4*b^2*c^4-a^4*c^6+a^2*b^8-3*a^2*b^6*c^2+4*a^2*b^4*c^4-3*a^2*b^2*c^6+a^2*c^8+b^8*c^2-b^6*c^4-b^4*c^6+b^2*c^8)*HY^2+(a^2+b^2+c^2)*(a^8*b^2-2*a^6*b^4-2*a^6*b^2*c^2+a^6*c^4+a^4*b^6+3*a^4*b^4*c^2+3*a^4*b^2*c^4-2*a^4*c^6-2*a^2*b^6*c^2+3*a^2*b^4*c^4-2*a^2*b^2*c^6+a^2*c^8+b^8*c^2-2*b^6*c^4+b^4*c^6)*(a^8*c^2+a^6*b^4-a^6*b^2*c^2-2*a^6*c^4-2*a^4*b^6+a^4*b^4*c^2+a^4*b^2*c^4+a^4*c^6+a^2*b^8-a^2*b^6*c^2+a^2*b^4*c^4-a^2*b^2*c^6+b^6*c^4-2*b^4*c^6+b^2*c^8)=0

4.  (a^2+b^2+c^2)*(a+b+c)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*IY^4+(a+b+c)*(a^7*c^2+a^6*b^3-2*a^6*b^2*c+2*a^5*b^3*c-2*a^5*b^2*c^2+2*a^5*b*c^3-2*a^5*c^4-2*a^4*b^5-2*a^4*b^4*c-2*a^4*b^3*c^2-a^4*b^2*c^3-2*a^4*b*c^4+2*a^3*b^5*c-a^3*b^4*c^2+6*a^3*b^3*c^3-2*a^3*b^2*c^4+2*a^3*b*c^5+a^3*c^6+a^2*b^7-2*a^2*b^5*c^2-2*a^2*b^4*c^3-a^2*b^3*c^4-2*a^2*b^2*c^5-2*a^2*b*c^6-2*a*b^6*c^2+2*a*b^5*c^3-2*a*b^4*c^4+2*a*b^3*c^5+b^6*c^3-2*b^4*c^5+b^2*c^7)*(a^2*b^2+a^2*c^2+b^2*c^2)*IY^2-a*b*c*(a^3*b-a^2*b^2-a^2*c^2+a*c^3+b^3*c-b^2*c^2)*(a^7*c^2+a^6*b^3-a^6*b^2*c+a^5*b^3*c-2*a^5*b^2*c^2+a^5*b*c^3-2*a^5*c^4-2*a^4*b^5-a^4*b^4*c-2*a^4*b^3*c^2-a^4*b*c^4+a^3*b^5*c+3*a^3*b^3*c^3-2*a^3*b^2*c^4+a^3*b*c^5+a^3*c^6+a^2*b^7-2*a^2*b^5*c^2-2*a^2*b^4*c^3-2*a^2*b^2*c^5-a^2*b*c^6-a*b^6*c^2+a*b^5*c^3-a*b^4*c^4+a*b^3*c^5+b^6*c^3-2*b^4*c^5+b^2*c^7)=0

5.  (a^2+b^2+c^2)*(-c+a-b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*O1Y^4+(-c+a-b)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^7*c^2-a^6*b^3+2*a^6*b^2*c+2*a^5*b^3*c-2*a^5*b^2*c^2+2*a^5*b*c^3-2*a^5*c^4+2*a^4*b^5+2*a^4*b^4*c+2*a^4*b^3*c^2+a^4*b^2*c^3+2*a^4*b*c^4+2*a^3*b^5*c-a^3*b^4*c^2+6*a^3*b^3*c^3-2*a^3*b^2*c^4+2*a^3*b*c^5+a^3*c^6-a^2*b^7+2*a^2*b^5*c^2+2*a^2*b^4*c^3+a^2*b^3*c^4+2*a^2*b^2*c^5+2*a^2*b*c^6-2*a*b^6*c^2+2*a*b^5*c^3-2*a*b^4*c^4+2*a*b^3*c^5-b^6*c^3+2*b^4*c^5-b^2*c^7)*O1Y^2+a*b*c*(a^3*b+a^2*b^2+a^2*c^2+a*c^3-b^3*c+b^2*c^2)*(a^7*c^2-a^6*b^3+a^6*b^2*c+a^5*b^3*c-2*a^5*b^2*c^2+a^5*b*c^3-2*a^5*c^4+2*a^4*b^5+a^4*b^4*c+2*a^4*b^3*c^2+a^4*b*c^4+a^3*b^5*c+3*a^3*b^3*c^3-2*a^3*b^2*c^4+a^3*b*c^5+a^3*c^6-a^2*b^7+2*a^2*b^5*c^2+2*a^2*b^4*c^3+2*a^2*b^2*c^5+a^2*b*c^6-a*b^6*c^2+a*b^5*c^3-a*b^4*c^4+a*b^3*c^5-b^6*c^3+2*b^4*c^5-b^2*c^7)=0

6.  (a^2+b^2+c^2)*(c+a-b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*O2Y^4+(c+a-b)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^7*c^2-a^6*b^3-2*a^6*b^2*c-2*a^5*b^3*c-2*a^5*b^2*c^2-2*a^5*b*c^3-2*a^5*c^4+2*a^4*b^5-2*a^4*b^4*c+2*a^4*b^3*c^2-a^4*b^2*c^3+2*a^4*b*c^4-2*a^3*b^5*c-a^3*b^4*c^2-6*a^3*b^3*c^3-2*a^3*b^2*c^4-2*a^3*b*c^5+a^3*c^6-a^2*b^7+2*a^2*b^5*c^2-2*a^2*b^4*c^3+a^2*b^3*c^4-2*a^2*b^2*c^5+2*a^2*b*c^6-2*a*b^6*c^2-2*a*b^5*c^3-2*a*b^4*c^4-2*a*b^3*c^5+b^6*c^3-2*b^4*c^5+b^2*c^7)*O2Y^2-a*b*c*(a^7*c^2-a^6*b^3-a^6*b^2*c-a^5*b^3*c-2*a^5*b^2*c^2-a^5*b*c^3-2*a^5*c^4+2*a^4*b^5-a^4*b^4*c+2*a^4*b^3*c^2+a^4*b*c^4-a^3*b^5*c-3*a^3*b^3*c^3-2*a^3*b^2*c^4-a^3*b*c^5+a^3*c^6-a^2*b^7+2*a^2*b^5*c^2-2*a^2*b^4*c^3-2*a^2*b^2*c^5+a^2*b*c^6-a*b^6*c^2-a*b^5*c^3-a*b^4*c^4-a*b^3*c^5+b^6*c^3-2*b^4*c^5+b^2*c^7)*(a^3*b+a^2*b^2+a^2*c^2-a*c^3+b^3*c+b^2*c^2)=0

7.  (a^2+b^2+c^2)*(-c+a+b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*O3Y^4+(-c+a+b)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^7*c^2+a^6*b^3+2*a^6*b^2*c-2*a^5*b^3*c-2*a^5*b^2*c^2-2*a^5*b*c^3-2*a^5*c^4-2*a^4*b^5+2*a^4*b^4*c-2*a^4*b^3*c^2+a^4*b^2*c^3-2*a^4*b*c^4-2*a^3*b^5*c-a^3*b^4*c^2-6*a^3*b^3*c^3-2*a^3*b^2*c^4-2*a^3*b*c^5+a^3*c^6+a^2*b^7-2*a^2*b^5*c^2+2*a^2*b^4*c^3-a^2*b^3*c^4+2*a^2*b^2*c^5-2*a^2*b*c^6-2*a*b^6*c^2-2*a*b^5*c^3-2*a*b^4*c^4-2*a*b^3*c^5-b^6*c^3+2*b^4*c^5-b^2*c^7)*O3Y^2+a*b*c*(a^3*b-a^2*b^2-a^2*c^2-a*c^3-b^3*c-b^2*c^2)*(a^7*c^2+a^6*b^3+a^6*b^2*c-a^5*b^3*c-2*a^5*b^2*c^2-a^5*b*c^3-2*a^5*c^4-2*a^4*b^5+a^4*b^4*c-2*a^4*b^3*c^2-a^4*b*c^4-a^3*b^5*c-3*a^3*b^3*c^3-2*a^3*b^2*c^4-a^3*b*c^5+a^3*c^6+a^2*b^7-2*a^2*b^5*c^2+2*a^2*b^4*c^3+2*a^2*b^2*c^5-a^2*b*c^6-a*b^6*c^2-a*b^5*c^3-a*b^4*c^4-a*b^3*c^5-b^6*c^3+2*b^4*c^5-b^2*c^7)=0

8. -(3*(a^2*b^2+a^2*c^2+b^2*c^2))*(2*a^8*b^2-a^8*c^2-5*a^6*b^4+a^6*b^2*c^2+4*a^6*c^4+4*a^4*b^6-a^4*b^4*c^2-a^4*b^2*c^4-5*a^4*c^6-a^2*b^8+a^2*b^6*c^2-a^2*b^4*c^4+a^2*b^2*c^6+2*a^2*c^8+2*b^8*c^2-5*b^6*c^4+4*b^4*c^6-b^2*c^8)*FY^2+(9*(a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4))*(a^2*b^2+a^2*c^2+b^2*c^2)^2*FY^4+2*c^4*b^10*a^2+2*a^4*b^2*c^10+3*a^4*b^6*c^6+3*a^6*b^4*c^6+3*a^6*b^6*c^4+2*a^10*c^4*b^2+2*c^10*b^4*a^2+2*c^2*a^10*b^4+2*b^10*a^4*c^2-4*c^4*b^8*a^4-4*c^4*a^8*b^4-4*c^8*a^4*b^4+b^4*a^12+a^12*c^4+c^12*b^4+b^12*c^4+a^4*b^12+a^4*c^12-4*a^6*c^10+6*b^8*a^8-4*b^10*a^6-4*c^10*b^6+6*c^8*b^8-4*b^10*c^6-4*c^6*a^10-4*b^6*a^10+6*c^8*a^8-a^8*b^2*c^6-a^8*b^6*c^2-a^2*b^6*c^8-a^6*b^2*c^8-a^6*b^8*c^2-a^2*b^8*c^6-a^12*b^2*c^2-c^2*a^2*b^12-a^2*b^2*c^12=0

9.  (16*(a^2+b^2+c^2))*(a+b+c)^2*(-c+a+b)^2*(-c+a-b)^2*(c+a-b)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*LY^4+(8*(a+b+c))*(-c+a+b)*(-c+a-b)*(c+a-b)*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^10*c^2-a^8*b^4-3*a^8*b^2*c^2-3*a^8*c^4+3*a^6*b^6+5*a^6*b^4*c^2+2*a^6*b^2*c^4+3*a^6*c^6-3*a^4*b^8+2*a^4*b^6*c^2+6*a^4*b^4*c^4+5*a^4*b^2*c^6-a^4*c^8+a^2*b^10-3*a^2*b^8*c^2+5*a^2*b^6*c^4+2*a^2*b^4*c^6-3*a^2*b^2*c^8-b^8*c^4+3*b^6*c^6-3*b^4*c^8+b^2*c^10)*LY^2-(a^2*b^2+a^2*c^2+b^2*c^2)*(a^8*b^2-a^8*c^2-3*a^6*b^4-a^6*b^2*c^2+3*a^6*c^4+3*a^4*b^6+a^4*b^4*c^2+a^4*b^2*c^4-3*a^4*c^6-a^2*b^8-a^2*b^6*c^2+a^2*b^4*c^4-a^2*b^2*c^6+a^2*c^8+b^8*c^2-3*b^6*c^4+3*b^4*c^6-b^2*c^8)*(a^8-4*a^6*b^2-4*a^6*c^2+6*a^4*b^4+5*a^4*b^2*c^2+6*a^4*c^4-4*a^2*b^6+5*a^2*b^4*c^2+5*a^2*b^2*c^4-4*a^2*c^6+b^8-4*b^6*c^2+6*b^4*c^4-4*b^2*c^6+c^8)=0

10. -72*b^6*c^18+16*b^4*c^20+168*b^7*c^17+129*b^8*c^16-(2*(a^2*b^2+a^2*c^2+b^2*c^2))*(a^2+b^2+c^2)*(3*a^14*b^2-12*a^14*c^2-40*a^13*b^3+20*a^13*b^2*c+12*a^13*b*c^2+12*a^13*c^3+99*a^12*b^4+28*a^12*b^3*c+7*a^12*b^2*c^2-40*a^12*b*c^3+63*a^12*c^4-52*a^11*b^5-200*a^11*b^4*c+32*a^11*b^3*c^2-80*a^11*b^2*c^3-52*a^11*b*c^4-88*a^11*c^5-22*a^10*b^6+92*a^10*b^5*c-a^10*b^4*c^2+224*a^10*b^3*c^3-3*a^10*b^2*c^4+228*a^10*b*c^5-33*a^10*c^6-96*a^9*b^7+232*a^9*b^6*c-20*a^9*b^5*c^2-28*a^9*b^4*c^3-376*a^9*b^3*c^4-12*a^9*b^2*c^5-40*a^9*b*c^6+8*a^9*c^7+158*a^8*b^8-40*a^8*b^7*c-207*a^8*b^6*c^2-184*a^8*b^5*c^3+563*a^8*b^4*c^4-44*a^8*b^3*c^5+78*a^8*b^2*c^6-240*a^8*b*c^7+158*a^8*c^8+8*a^7*b^9-240*a^7*b^8*c+176*a^7*b^7*c^2+16*a^7*b^6*c^3+64*a^7*b^5*c^4-464*a^7*b^4*c^5+256*a^7*b^3*c^6+176*a^7*b^2*c^7-40*a^7*b*c^8-96*a^7*c^9-33*a^6*b^10-40*a^6*b^9*c+78*a^6*b^8*c^2+256*a^6*b^7*c^3-228*a^6*b^6*c^4+240*a^6*b^5*c^5-228*a^6*b^4*c^6+16*a^6*b^3*c^7-207*a^6*b^2*c^8+232*a^6*b*c^9-22*a^6*c^10-88*a^5*b^11+228*a^5*b^10*c-12*a^5*b^9*c^2-44*a^5*b^8*c^3-464*a^5*b^7*c^4+240*a^5*b^6*c^5+240*a^5*b^5*c^6+64*a^5*b^4*c^7-184*a^5*b^3*c^8-20*a^5*b^2*c^9+92*a^5*b*c^10-52*a^5*c^11+63*a^4*b^12-52*a^4*b^11*c-3*a^4*b^10*c^2-376*a^4*b^9*c^3+563*a^4*b^8*c^4+64*a^4*b^7*c^5-228*a^4*b^6*c^6-464*a^4*b^5*c^7+563*a^4*b^4*c^8-28*a^4*b^3*c^9-a^4*b^2*c^10-200*a^4*b*c^11+99*a^4*c^12+12*a^3*b^13-40*a^3*b^12*c-80*a^3*b^11*c^2+224*a^3*b^10*c^3-28*a^3*b^9*c^4-184*a^3*b^8*c^5+16*a^3*b^7*c^6+256*a^3*b^6*c^7-44*a^3*b^5*c^8-376*a^3*b^4*c^9+224*a^3*b^3*c^10+32*a^3*b^2*c^11+28*a^3*b*c^12-40*a^3*c^13-12*a^2*b^14+12*a^2*b^13*c+7*a^2*b^12*c^2+32*a^2*b^11*c^3-a^2*b^10*c^4-20*a^2*b^9*c^5-207*a^2*b^8*c^6+176*a^2*b^7*c^7+78*a^2*b^6*c^8-12*a^2*b^5*c^9-3*a^2*b^4*c^10-80*a^2*b^3*c^11+7*a^2*b^2*c^12+20*a^2*b*c^13+3*a^2*c^14+20*a*b^13*c^2+28*a*b^12*c^3-200*a*b^11*c^4+92*a*b^10*c^5+232*a*b^9*c^6-40*a*b^8*c^7-240*a*b^7*c^8-40*a*b^6*c^9+228*a*b^5*c^10-52*a*b^4*c^11-40*a*b^3*c^12+12*a*b^2*c^13+3*b^14*c^2-40*b^13*c^3+99*b^12*c^4-52*b^11*c^5-22*b^10*c^6-96*b^9*c^7+158*b^8*c^8+8*b^7*c^9-33*b^6*c^10-88*b^5*c^11+63*b^4*c^12+12*b^3*c^13-12*b^2*c^14)*JY^2+a^20*b^4+16*a^20*c^4-8*a^19*b^5-32*a^19*c^5+70*a^18*b^6-72*a^18*c^6-224*a^17*b^7+168*a^17*c^7+223*a^16*b^8+129*a^16*c^8+88*a^15*b^9-384*a^15*c^9-84*a^14*b^10-42*a^14*c^10-384*a^13*b^11+264*a^13*c^11+271*a^12*b^12+271*a^12*c^12+264*a^11*b^13-384*a^11*c^13-42*a^10*b^14-84*a^10*c^14-384*a^9*b^15+88*a^9*c^15+129*a^8*b^16+223*a^8*c^16+168*a^7*b^17-224*a^7*c^17-72*a^6*b^18+70*a^6*c^18-32*a^5*b^19-8*a^5*c^19+16*a^4*b^20+a^4*c^20+b^20*c^4-8*b^19*c^5+70*b^18*c^6-224*b^17*c^7+223*b^16*c^8+88*b^15*c^9-84*b^14*c^10-384*b^13*c^11+271*b^12*c^12+264*b^11*c^13-42*b^10*c^14-384*b^9*c^15-8*a^20*b^2*c^2+40*a^19*b^3*c^2+8*a^19*b^2*c^3-32*a^19*b*c^4-64*a^18*b^5*c-10*a^18*b^4*c^2-80*a^18*b^3*c^3-30*a^18*b^2*c^4+128*a^18*b*c^5+96*a^17*b^6*c-48*a^17*b^5*c^2+136*a^17*b^4*c^3-16*a^17*b^3*c^4+8*a^17*b*c^6+376*a^16*b^7*c-240*a^16*b^6*c^2+352*a^16*b^5*c^3+99*a^16*b^4*c^4-64*a^16*b^3*c^5+268*a^16*b^2*c^6-528*a^16*b*c^7-752*a^15*b^8*c+208*a^15*b^7*c^2-784*a^15*b^6*c^3-296*a^15*b^5*c^4-712*a^15*b^4*c^5+96*a^15*b^3*c^6-16*a^15*b^2*c^7+248*a^15*b*c^8-312*a^14*b^9*c+792*a^14*b^8*c^2-80*a^14*b^7*c^3+1430*a^14*b^6*c^4+720*a^14*b^5*c^5+242*a^14*b^4*c^6+544*a^14*b^3*c^7-636*a^14*b^2*c^8+1024*a^14*b*c^9+1056*a^13*b^10*c-352*a^13*b^9*c^2+272*a^13*b^8*c^3-1704*a^13*b^7*c^4-240*a^13*b^6*c^5-1152*a^13*b^5*c^6+328*a^13*b^4*c^7-672*a^13*b^3*c^8-432*a^13*b^2*c^9-656*a^13*b*c^10+432*a^12*b^11*c-1518*a^12*b^10*c^2+720*a^12*b^9*c^3+39*a^12*b^8*c^4+1560*a^12*b^7*c^5-322*a^12*b^6*c^6+152*a^12*b^5*c^7+554*a^12*b^4*c^8+488*a^12*b^3*c^9+1390*a^12*b^2*c^10-1024*a^12*b*c^11-1024*a^11*b^12*c+592*a^11*b^11*c^2-8*a^11*b^10*c^3+280*a^11*b^9*c^4-1776*a^11*b^8*c^5+752*a^11*b^7*c^6-352*a^11*b^6*c^7+504*a^11*b^5*c^8-1376*a^11*b^4*c^9-872*a^11*b^3*c^10+592*a^11*b^2*c^11+432*a^11*b*c^12-656*a^10*b^13*c+1390*a^10*b^12*c^2-872*a^10*b^11*c^3+952*a^10*b^10*c^4+64*a^10*b^9*c^5+648*a^10*b^8*c^6-288*a^10*b^7*c^7+122*a^10*b^6*c^8+192*a^10*b^5*c^9+952*a^10*b^4*c^10-8*a^10*b^3*c^11-1518*a^10*b^2*c^12+1056*a^10*b*c^13+1024*a^9*b^14*c-432*a^9*b^13*c^2+488*a^9*b^12*c^3-1376*a^9*b^11*c^4+192*a^9*b^10*c^5-248*a^9*b^9*c^6-256*a^9*b^8*c^7-352*a^9*b^7*c^8-248*a^9*b^6*c^9+64*a^9*b^5*c^10+280*a^9*b^4*c^11+720*a^9*b^3*c^12-352*a^9*b^2*c^13-312*a^9*b*c^14+248*a^8*b^15*c-636*a^8*b^14*c^2-672*a^8*b^13*c^3+554*a^8*b^12*c^4+504*a^8*b^11*c^5+122*a^8*b^10*c^6-352*a^8*b^9*c^7+1269*a^8*b^8*c^8-256*a^8*b^7*c^9+648*a^8*b^6*c^10-1776*a^8*b^5*c^11+39*a^8*b^4*c^12+272*a^8*b^3*c^13+792*a^8*b^2*c^14-752*a^8*b*c^15-528*a^7*b^16*c-16*a^7*b^15*c^2+544*a^7*b^14*c^3+328*a^7*b^13*c^4+152*a^7*b^12*c^5-352*a^7*b^11*c^6-288*a^7*b^10*c^7-256*a^7*b^9*c^8-352*a^7*b^8*c^9-288*a^7*b^7*c^10+752*a^7*b^6*c^11+1560*a^7*b^5*c^12-1704*a^7*b^4*c^13-80*a^7*b^3*c^14+208*a^7*b^2*c^15+376*a^7*b*c^16+8*a^6*b^17*c+268*a^6*b^16*c^2+96*a^6*b^15*c^3+242*a^6*b^14*c^4-1152*a^6*b^13*c^5-322*a^6*b^12*c^6+752*a^6*b^11*c^7+648*a^6*b^10*c^8-248*a^6*b^9*c^9+122*a^6*b^8*c^10-352*a^6*b^7*c^11-322*a^6*b^6*c^12-240*a^6*b^5*c^13+1430*a^6*b^4*c^14-784*a^6*b^3*c^15-240*a^6*b^2*c^16+96*a^6*b*c^17+128*a^5*b^18*c-64*a^5*b^16*c^3-712*a^5*b^15*c^4+720*a^5*b^14*c^5-240*a^5*b^13*c^6+1560*a^5*b^12*c^7-1776*a^5*b^11*c^8+64*a^5*b^10*c^9+192*a^5*b^9*c^10+504*a^5*b^8*c^11+152*a^5*b^7*c^12-1152*a^5*b^6*c^13+720*a^5*b^5*c^14-296*a^5*b^4*c^15+352*a^5*b^3*c^16-48*a^5*b^2*c^17-64*a^5*b*c^18-32*a^4*b^19*c-30*a^4*b^18*c^2-16*a^4*b^17*c^3+99*a^4*b^16*c^4-296*a^4*b^15*c^5+1430*a^4*b^14*c^6-1704*a^4*b^13*c^7+39*a^4*b^12*c^8+280*a^4*b^11*c^9+952*a^4*b^10*c^10-1376*a^4*b^9*c^11+554*a^4*b^8*c^12+328*a^4*b^7*c^13+242*a^4*b^6*c^14-712*a^4*b^5*c^15+99*a^4*b^4*c^16+136*a^4*b^3*c^17-10*a^4*b^2*c^18+8*a^3*b^19*c^2-80*a^3*b^18*c^3+136*a^3*b^17*c^4+352*a^3*b^16*c^5-784*a^3*b^15*c^6-80*a^3*b^14*c^7+272*a^3*b^13*c^8+720*a^3*b^12*c^9-8*a^3*b^11*c^10-872*a^3*b^10*c^11+488*a^3*b^9*c^12-672*a^3*b^8*c^13+544*a^3*b^7*c^14+96*a^3*b^6*c^15-64*a^3*b^5*c^16-16*a^3*b^4*c^17-80*a^3*b^3*c^18+40*a^3*b^2*c^19-8*a^2*b^20*c^2+40*a^2*b^19*c^3-10*a^2*b^18*c^4-48*a^2*b^17*c^5-240*a^2*b^16*c^6+208*a^2*b^15*c^7+792*a^2*b^14*c^8-352*a^2*b^13*c^9-1518*a^2*b^12*c^10+592*a^2*b^11*c^11+1390*a^2*b^10*c^12-432*a^2*b^9*c^13-636*a^2*b^8*c^14-16*a^2*b^7*c^15+268*a^2*b^6*c^16-30*a^2*b^4*c^18+8*a^2*b^3*c^19-8*a^2*b^2*c^20-64*a*b^18*c^5+96*a*b^17*c^6+376*a*b^16*c^7-752*a*b^15*c^8-312*a*b^14*c^9+1056*a*b^13*c^10+432*a*b^12*c^11-1024*a*b^11*c^12-656*a*b^10*c^13+1024*a*b^9*c^14+248*a*b^8*c^15-528*a*b^7*c^16+8*a*b^6*c^17+128*a*b^5*c^18-32*a*b^4*c^19-32*b^5*c^19+(a^2+b^2+c^2)^2*(a^2*b^2+a^2*c^2+b^2*c^2)^2*(5*a^4-4*a^3*b-4*a^3*c-2*a^2*b^2+4*a^2*b*c-2*a^2*c^2-4*a*b^3+4*a*b^2*c+4*a*b*c^2-4*a*c^3+5*b^4-4*b^3*c-2*b^2*c^2-4*b*c^3+5*c^4)^2*JY^4=0

11. (a^2+b^2+c^2)*(a^2*b^2+a^2*c^2+b^2*c^2)^3*XY^4-a^2*b^2*c^2*(a^2*b^2+a^2*c^2+b^2*c^2)*(a^2+b^2+c^2)*(a^4+b^4+c^4)*XY^2+b^4*c^4*a^4*(a^2+b^2+c^2)*(a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)=0

数学星空

关于等力点S,T的心距公式：

1.  (a^12-5*a^10*b^2-5*a^10*c^2+11*a^8*b^4+11*a^8*b^2*c^2+11*a^8*c^4-14*a^6*b^6-6*a^6*b^4*c^2-6*a^6*b^2*c^4-14*a^6*c^6+11*a^4*b^8-6*a^4*b^6*c^2+6*a^4*b^4*c^4-6*a^4*b^2*c^6+11*a^4*c^8-5*a^2*b^10+11*a^2*b^8*c^2-6*a^2*b^6*c^4-6*a^2*b^4*c^6+11*a^2*b^2*c^8-5*a^2*c^10+b^12-5*b^10*c^2+11*b^8*c^4-14*b^6*c^6+11*b^4*c^8-5*b^2*c^10+c^12)*OS^4+(-a^10*b^2*c^2+6*a^8*b^4*c^2+6*a^8*b^2*c^4-10*a^6*b^6*c^2-10*a^6*b^4*c^4-10*a^6*b^2*c^6+6*a^4*b^8*c^2-10*a^4*b^6*c^4-10*a^4*b^4*c^6+6*a^4*b^2*c^8-a^2*b^10*c^2+6*a^2*b^8*c^4-10*a^2*b^6*c^6+6*a^2*b^4*c^8-a^2*b^2*c^10)*OS^2-c^6*b^6*a^4+a^8*b^4*c^4-c^4*b^6*a^6+a^4*c^8*b^4+a^4*b^8*c^4-c^6*a^6*b^4=0

2.  (81*a^4-81*a^2*b^2-81*a^2*c^2+81*b^4-81*b^2*c^2+81*c^4)*GS^4+(9*(a^2+b^2+c^2))*(2*a^4-5*a^2*b^2-5*a^2*c^2+2*b^4-5*b^2*c^2+2*c^4)*GS^2+(a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)^2=0

3.   (a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)*(-c+a+b)^2*(a+b+c)^2*(c+a-b)^2*(-c+a-b)^2*HS^4+(a+b+c)*(-c+a+b)*(-c+a-b)*(c+a-b)*(2*a^10-5*a^8*b^2-5*a^8*c^2+3*a^6*b^4+5*a^6*b^2*c^2+3*a^6*c^4+3*a^4*b^6+3*a^4*c^6-5*a^2*b^8+5*a^2*b^6*c^2+5*a^2*b^2*c^6-5*a^2*c^8+2*b^10-5*b^8*c^2+3*b^6*c^4+3*b^4*c^6-5*b^2*c^8+2*c^10)*HS^2-4*a^8*c^8+5*c^12*a^4+5*c^12*b^4+5*a^12*b^4-4*a^8*b^8-4*a^14*b^2+5*a^12*c^4-4*a^14*c^2+5*b^12*c^4-4*c^14*b^2-4*c^8*b^8-4*c^14*a^2-4*b^14*a^2+5*a^4*b^12-4*b^14*c^2+a^16+b^16+c^16+9*a^4*c^8*b^4+9*a^8*b^4*c^4+4*a^6*b^8*c^2+4*a^6*c^8*b^2+9*a^4*b^8*c^4+4*a^8*b^2*c^6+4*a^8*b^6*c^2+12*a^2*c^2*b^12+12*a^2*c^12*b^2+4*a^2*b^6*c^8+4*a^2*b^8*c^6-4*c^4*b^6*a^6-12*a^4*b^2*c^10-12*a^4*b^10*c^2-12*a^10*b^4*c^2-12*a^10*b^2*c^4-12*a^2*b^4*c^10-12*a^2*b^10*c^4+12*a^12*b^2*c^2-4*c^6*a^6*b^4-4*c^6*b^6*a^4=0

4.   (a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)*(a+b+c)^2*IS^4+b*a*c*(a+b+c)*(2*a^4-a^3*b-a^3*c-2*a^2*b^2-a^2*b*c-2*a^2*c^2-a*b^3-a*b^2*c-a*b*c^2-a*c^3+2*b^4-b^3*c-2*b^2*c^2-b*c^3+2*c^4)*IS^2+a^2*b^2*c^2*(a^4-a^3*b-a^3*c+a^2*b*c-a*b^3+a*b^2*c+a*b*c^2-a*c^3+b^4-b^3*c-b*c^3+c^4)=0

5.   (a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)*(a-b-c)^2*O1S^4+b*a*c*(a-b-c)*(2*a^4+a^3*b+a^3*c-2*a^2*b^2-a^2*b*c-2*a^2*c^2+a*b^3+a*b^2*c+a*b*c^2+a*c^3+2*b^4-b^3*c-2*b^2*c^2-b*c^3+2*c^4)*O1S^2+a^2*b^2*c^2*(a^4+a^3*b+a^3*c+a^2*b*c+a*b^3-a*b^2*c-a*b*c^2+a*c^3+b^4-b^3*c-b*c^3+c^4)=0

6.   (a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)*(-b+c+a)^2*O2S^4-b*a*c*(-b+c+a)*(2*a^4+a^3*b-a^3*c-2*a^2*b^2+a^2*b*c-2*a^2*c^2+a*b^3-a*b^2*c+a*b*c^2-a*c^3+2*b^4+b^3*c-2*b^2*c^2+b*c^3+2*c^4)*O2S^2+a^2*b^2*c^2*(a^4+a^3*b-a^3*c-a^2*b*c+a*b^3+a*b^2*c-a*b*c^2-a*c^3+b^4+b^3*c+b*c^3+c^4)=0

7.   (a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)*(-c+a+b)^2*O3S^4-b*a*c*(-c+a+b)*(2*a^4-a^3*b+a^3*c-2*a^2*b^2+a^2*b*c-2*a^2*c^2-a*b^3+a*b^2*c-a*b*c^2+a*c^3+2*b^4+b^3*c-2*b^2*c^2+b*c^3+2*c^4)*O3S^2+a^2*b^2*c^2*(a^4-a^3*b+a^3*c-a^2*b*c-a*b^3-a*b^2*c+a*b*c^2+a*c^3+b^4+b^3*c+b*c^3+c^4)=0

8.   9*(a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)^2*FS^4+(3*(a^4-4*a^2*b^2-4*a^2*c^2+b^4-4*b^2*c^2+c^4))*(a^6-a^4*b^2-a^4*c^2-a^2*b^4+3*a^2*b^2*c^2-a^2*c^4+b^6-b^4*c^2-b^2*c^4+c^6)*FS^2+(a^6-a^4*b^2-a^4*c^2-a^2*b^4+3*a^2*b^2*c^2-a^2*c^4+b^6-b^4*c^2-b^2*c^4+c^6)^2=0

9.  -11*a^6*c^10+10*a^8*c^8-5*a^14*b^2-5*a^14*c^2-5*a^2*b^14-5*a^2*c^14-5*b^14*c^2-5*b^2*c^14+10*b^4*c^12+10*b^12*c^4+10*b^8*c^8-11*b^10*c^6-11*b^6*c^10-11*a^6*b^10+10*a^4*b^12+10*a^12*b^4-11*a^10*b^6+10*a^8*b^8+10*a^4*c^12+10*a^12*c^4-11*a^10*c^6+c^16+b^16+a^16+a^4*b^6*c^6+a^6*b^6*c^4+a^6*b^4*c^6+5*a^8*b^6*c^2+5*a^4*b^8*c^4+5*a^2*b^6*c^8+5*a^4*b^4*c^8-15*a^10*b^4*c^2+5*a^6*b^2*c^8-15*a^2*b^4*c^10-15*a^4*b^10*c^2+15*a^12*b^2*c^2+15*a^2*b^2*c^12+5*a^8*b^4*c^4-15*a^10*b^2*c^4+5*a^8*b^2*c^6+15*a^2*b^12*c^2-15*a^2*b^10*c^4+5*a^6*b^8*c^2-15*a^4*b^2*c^10+5*a^2*b^8*c^6+(16*(a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4))*(-c+a+b)^2*(a+b+c)^2*(-b+c+a)^2*(a-b-c)^2*LS^4+(8*(a+b+c))*(-c+a+b)*(a-b-c)*(-b+c+a)*(a^10-3*a^8*b^2-3*a^8*c^2+2*a^6*b^4+2*a^6*c^4+2*a^4*b^6+7*a^4*b^4*c^2+7*a^4*b^2*c^4+2*a^4*c^6-3*a^2*b^8+7*a^2*b^4*c^4-3*a^2*c^8+b^10-3*b^8*c^2+2*b^6*c^4+2*b^4*c^6-3*b^2*c^8+c^10)*LS^2=0

10.  (a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)^2*(5*a^4-4*a^3*b-4*a^3*c-2*a^2*b^2+4*a^2*b*c-2*a^2*c^2-4*a*b^3+4*a*b^2*c+4*a*b*c^2-4*a*c^3+5*b^4-4*b^3*c-2*b^2*c^2-4*b*c^3+5*c^4)^4*JS^8-(2*(6*a^14-20*a^13*b-20*a^13*c+13*a^12*b^2+56*a^12*b*c+13*a^12*c^2+12*a^11*b^3-18*a^11*b^2*c-18*a^11*b*c^2+12*a^11*c^3+21*a^10*b^4-58*a^10*b^3*c-21*a^10*b^2*c^2-58*a^10*b*c^3+21*a^10*c^4-92*a^9*b^5+70*a^9*b^3*c^2+70*a^9*b^2*c^3-92*a^9*c^5+88*a^8*b^6+108*a^8*b^5*c-81*a^8*b^4*c^2-20*a^8*b^3*c^3-81*a^8*b^2*c^4+108*a^8*b*c^5+88*a^8*c^6-56*a^7*b^7-68*a^7*b^6*c+12*a^7*b^5*c^2+40*a^7*b^4*c^3+40*a^7*b^3*c^4+12*a^7*b^2*c^5-68*a^7*b*c^6-56*a^7*c^7+88*a^6*b^8-68*a^6*b^7*c+50*a^6*b^6*c^2-44*a^6*b^5*c^3+12*a^6*b^4*c^4-44*a^6*b^3*c^5+50*a^6*b^2*c^6-68*a^6*b*c^7+88*a^6*c^8-92*a^5*b^9+108*a^5*b^8*c+12*a^5*b^7*c^2-44*a^5*b^6*c^3+16*a^5*b^5*c^4+16*a^5*b^4*c^5-44*a^5*b^3*c^6+12*a^5*b^2*c^7+108*a^5*b*c^8-92*a^5*c^9+21*a^4*b^10-81*a^4*b^8*c^2+40*a^4*b^7*c^3+12*a^4*b^6*c^4+16*a^4*b^5*c^5+12*a^4*b^4*c^6+40*a^4*b^3*c^7-81*a^4*b^2*c^8+21*a^4*c^10+12*a^3*b^11-58*a^3*b^10*c+70*a^3*b^9*c^2-20*a^3*b^8*c^3+40*a^3*b^7*c^4-44*a^3*b^6*c^5-44*a^3*b^5*c^6+40*a^3*b^4*c^7-20*a^3*b^3*c^8+70*a^3*b^2*c^9-58*a^3*b*c^10+12*a^3*c^11+13*a^2*b^12-18*a^2*b^11*c-21*a^2*b^10*c^2+70*a^2*b^9*c^3-81*a^2*b^8*c^4+12*a^2*b^7*c^5+50*a^2*b^6*c^6+12*a^2*b^5*c^7-81*a^2*b^4*c^8+70*a^2*b^3*c^9-21*a^2*b^2*c^10-18*a^2*b*c^11+13*a^2*c^12-20*a*b^13+56*a*b^12*c-18*a*b^11*c^2-58*a*b^10*c^3+108*a*b^8*c^5-68*a*b^7*c^6-68*a*b^6*c^7+108*a*b^5*c^8-58*a*b^3*c^10-18*a*b^2*c^11+56*a*b*c^12-20*a*c^13+6*b^14-20*b^13*c+13*b^12*c^2+12*b^11*c^3+21*b^10*c^4-92*b^9*c^5+88*b^8*c^6-56*b^7*c^7+88*b^6*c^8-92*b^5*c^9+21*b^4*c^10+12*b^3*c^11+13*b^2*c^12-20*b*c^13+6*c^14))*(a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)*(5*a^4-4*a^3*b-4*a^3*c-2*a^2*b^2+4*a^2*b*c-2*a^2*c^2-4*a*b^3+4*a*b^2*c+4*a*b*c^2-4*a*c^3+5*b^4-4*b^3*c-2*b^2*c^2-4*b*c^3+5*c^4)^2*JS^6+(86*a^28-520*a^27*b-520*a^27*c+1018*a^26*b^2+3056*a^26*b*c+1018*a^26*c^2-332*a^25*b^3-5592*a^25*b^2*c-5592*a^25*b*c^2-332*a^25*c^3-599*a^24*b^4+372*a^24*b^3*c+8484*a^24*b^2*c^2+372*a^24*b*c^3-599*a^24*c^4-2120*a^23*b^5+6960*a^23*b^4*c+6144*a^23*b^3*c^2+6144*a^23*b^2*c^3+6960*a^23*b*c^4-2120*a^23*c^5+7772*a^22*b^6+5192*a^22*b^5*c-25210*a^22*b^4*c^2-24624*a^22*b^3*c^3-25210*a^22*b^2*c^4+5192*a^22*b*c^5+7772*a^22*c^6-11704*a^21*b^7-25960*a^21*b^6*c+5320*a^21*b^5*c^2+37132*a^21*b^4*c^3+37132*a^21*b^3*c^4+5320*a^21*b^2*c^5-25960*a^21*b*c^6-11704*a^21*c^7+14433*a^20*b^8+24240*a^20*b^7*c+22574*a^20*b^6*c^2-16884*a^20*b^5*c^3-12815*a^20*b^4*c^4-16884*a^20*b^3*c^5+22574*a^20*b^2*c^6+24240*a^20*b*c^7+14433*a^20*c^8-16028*a^19*b^9-20460*a^19*b^8*c+17120*a^19*b^7*c^2-5664*a^19*b^6*c^3-22756*a^19*b^5*c^4-22756*a^19*b^4*c^5-5664*a^19*b^3*c^6+17120*a^19*b^2*c^7-20460*a^19*b*c^8-16028*a^19*c^9+17446*a^18*b^10+27064*a^18*b^9*c-61448*a^18*b^8*c^2-35184*a^18*b^7*c^3+32414*a^18*b^6*c^4+72584*a^18*b^5*c^5+32414*a^18*b^4*c^6-35184*a^18*b^3*c^7-61448*a^18*b^2*c^8+27064*a^18*b*c^9+17446*a^18*c^10-28912*a^17*b^11-7568*a^17*b^10*c+37048*a^17*b^9*c^2+96732*a^17*b^8*c^3-56816*a^17*b^7*c^4-35400*a^17*b^6*c^5-35400*a^17*b^5*c^6-56816*a^17*b^4*c^7+96732*a^17*b^3*c^8+37048*a^17*b^2*c^9-7568*a^17*b*c^10-28912*a^17*c^11+43296*a^16*b^12-96*a^16*b^11*c-56534*a^16*b^10*c^2-71524*a^16*b^9*c^3+96699*a^16*b^8*c^4+21800*a^16*b^7*c^5-58284*a^16*b^6*c^6+21800*a^16*b^5*c^7+96699*a^16*b^4*c^8-71524*a^16*b^3*c^9-56534*a^16*b^2*c^10-96*a^16*b*c^11+43296*a^16*c^12-38688*a^15*b^13-42752*a^15*b^12*c+127264*a^15*b^11*c^2+15216*a^15*b^10*c^3-71456*a^15*b^9*c^4-138080*a^15*b^8*c^5+127008*a^15*b^7*c^6+127008*a^15*b^6*c^7-138080*a^15*b^5*c^8-71456*a^15*b^4*c^9+15216*a^15*b^3*c^10+127264*a^15*b^2*c^11-42752*a^15*b*c^12-38688*a^15*c^13+29704*a^14*b^14+36064*a^14*b^13*c-85492*a^14*b^12*c^2-29616*a^14*b^11*c^3+51356*a^14*b^10*c^4+124576*a^14*b^9*c^5-112864*a^14*b^8*c^6+15168*a^14*b^7*c^7-112864*a^14*b^6*c^8+124576*a^14*b^5*c^9+51356*a^14*b^4*c^10-29616*a^14*b^3*c^11-85492*a^14*b^2*c^12+36064*a^14*b*c^13+29704*a^14*c^14-38688*a^13*b^15+36064*a^13*b^14*c+18608*a^13*b^13*c^2+28232*a^13*b^12*c^3-163400*a^13*b^11*c^4+103440*a^13*b^10*c^5+141104*a^13*b^9*c^6-134576*a^13*b^8*c^7-134576*a^13*b^7*c^8+141104*a^13*b^6*c^9+103440*a^13*b^5*c^10-163400*a^13*b^4*c^11+28232*a^13*b^3*c^12+18608*a^13*b^2*c^13+36064*a^13*b*c^14-38688*a^13*c^15+43296*a^12*b^16-42752*a^12*b^15*c-85492*a^12*b^14*c^2+28232*a^12*b^13*c^3+256982*a^12*b^12*c^4-117672*a^12*b^11*c^5-247964*a^12*b^10*c^6-169472*a^12*b^9*c^7+673780*a^12*b^8*c^8-169472*a^12*b^7*c^9-247964*a^12*b^6*c^10-117672*a^12*b^5*c^11+256982*a^12*b^4*c^12+28232*a^12*b^3*c^13-85492*a^12*b^2*c^14-42752*a^12*b*c^15+43296*a^12*c^16-28912*a^11*b^17-96*a^11*b^16*c+127264*a^11*b^15*c^2-29616*a^11*b^14*c^3-163400*a^11*b^13*c^4-117672*a^11*b^12*c^5+310528*a^11*b^11*c^6+202416*a^11*b^10*c^7-300512*a^11*b^9*c^8-300512*a^11*b^8*c^9+202416*a^11*b^7*c^10+310528*a^11*b^6*c^11-117672*a^11*b^5*c^12-163400*a^11*b^4*c^13-29616*a^11*b^3*c^14+127264*a^11*b^2*c^15-96*a^11*b*c^16-28912*a^11*c^17+17446*a^10*b^18-7568*a^10*b^17*c-56534*a^10*b^16*c^2+15216*a^10*b^15*c^3+51356*a^10*b^14*c^4+103440*a^10*b^13*c^5-247964*a^10*b^12*c^6+202416*a^10*b^11*c^7-227408*a^10*b^10*c^8+299200*a^10*b^9*c^9-227408*a^10*b^8*c^10+202416*a^10*b^7*c^11-247964*a^10*b^6*c^12+103440*a^10*b^5*c^13+51356*a^10*b^4*c^14+15216*a^10*b^3*c^15-56534*a^10*b^2*c^16-7568*a^10*b*c^17+17446*a^10*c^18-16028*a^9*b^19+27064*a^9*b^18*c+37048*a^9*b^17*c^2-71524*a^9*b^16*c^3-71456*a^9*b^15*c^4+124576*a^9*b^14*c^5+141104*a^9*b^13*c^6-169472*a^9*b^12*c^7-300512*a^9*b^11*c^8+299200*a^9*b^10*c^9+299200*a^9*b^9*c^10-300512*a^9*b^8*c^11-169472*a^9*b^7*c^12+141104*a^9*b^6*c^13+124576*a^9*b^5*c^14-71456*a^9*b^4*c^15-71524*a^9*b^3*c^16+37048*a^9*b^2*c^17+27064*a^9*b*c^18-16028*a^9*c^19+14433*a^8*b^20-20460*a^8*b^19*c-61448*a^8*b^18*c^2+96732*a^8*b^17*c^3+96699*a^8*b^16*c^4-138080*a^8*b^15*c^5-112864*a^8*b^14*c^6-134576*a^8*b^13*c^7+673780*a^8*b^12*c^8-300512*a^8*b^11*c^9-227408*a^8*b^10*c^10-300512*a^8*b^9*c^11+673780*a^8*b^8*c^12-134576*a^8*b^7*c^13-112864*a^8*b^6*c^14-138080*a^8*b^5*c^15+96699*a^8*b^4*c^16+96732*a^8*b^3*c^17-61448*a^8*b^2*c^18-20460*a^8*b*c^19+14433*a^8*c^20-11704*a^7*b^21+24240*a^7*b^20*c+17120*a^7*b^19*c^2-35184*a^7*b^18*c^3-56816*a^7*b^17*c^4+21800*a^7*b^16*c^5+127008*a^7*b^15*c^6+15168*a^7*b^14*c^7-134576*a^7*b^13*c^8-169472*a^7*b^12*c^9+202416*a^7*b^11*c^10+202416*a^7*b^10*c^11-169472*a^7*b^9*c^12-134576*a^7*b^8*c^13+15168*a^7*b^7*c^14+127008*a^7*b^6*c^15+21800*a^7*b^5*c^16-56816*a^7*b^4*c^17-35184*a^7*b^3*c^18+17120*a^7*b^2*c^19+24240*a^7*b*c^20-11704*a^7*c^21+7772*a^6*b^22-25960*a^6*b^21*c+22574*a^6*b^20*c^2-5664*a^6*b^19*c^3+32414*a^6*b^18*c^4-35400*a^6*b^17*c^5-58284*a^6*b^16*c^6+127008*a^6*b^15*c^7-112864*a^6*b^14*c^8+141104*a^6*b^13*c^9-247964*a^6*b^12*c^10+310528*a^6*b^11*c^11-247964*a^6*b^10*c^12+141104*a^6*b^9*c^13-112864*a^6*b^8*c^14+127008*a^6*b^7*c^15-58284*a^6*b^6*c^16-35400*a^6*b^5*c^17+32414*a^6*b^4*c^18-5664*a^6*b^3*c^19+22574*a^6*b^2*c^20-25960*a^6*b*c^21+7772*a^6*c^22-2120*a^5*b^23+5192*a^5*b^22*c+5320*a^5*b^21*c^2-16884*a^5*b^20*c^3-22756*a^5*b^19*c^4+72584*a^5*b^18*c^5-35400*a^5*b^17*c^6+21800*a^5*b^16*c^7-138080*a^5*b^15*c^8+124576*a^5*b^14*c^9+103440*a^5*b^13*c^10-117672*a^5*b^12*c^11-117672*a^5*b^11*c^12+103440*a^5*b^10*c^13+124576*a^5*b^9*c^14-138080*a^5*b^8*c^15+21800*a^5*b^7*c^16-35400*a^5*b^6*c^17+72584*a^5*b^5*c^18-22756*a^5*b^4*c^19-16884*a^5*b^3*c^20+5320*a^5*b^2*c^21+5192*a^5*b*c^22-2120*a^5*c^23-599*a^4*b^24+6960*a^4*b^23*c-25210*a^4*b^22*c^2+37132*a^4*b^21*c^3-12815*a^4*b^20*c^4-22756*a^4*b^19*c^5+32414*a^4*b^18*c^6-56816*a^4*b^17*c^7+96699*a^4*b^16*c^8-71456*a^4*b^15*c^9+51356*a^4*b^14*c^10-163400*a^4*b^13*c^11+256982*a^4*b^12*c^12-163400*a^4*b^11*c^13+51356*a^4*b^10*c^14-71456*a^4*b^9*c^15+96699*a^4*b^8*c^16-56816*a^4*b^7*c^17+32414*a^4*b^6*c^18-22756*a^4*b^5*c^19-12815*a^4*b^4*c^20+37132*a^4*b^3*c^21-25210*a^4*b^2*c^22+6960*a^4*b*c^23-599*a^4*c^24-332*a^3*b^25+372*a^3*b^24*c+6144*a^3*b^23*c^2-24624*a^3*b^22*c^3+37132*a^3*b^21*c^4-16884*a^3*b^20*c^5-5664*a^3*b^19*c^6-35184*a^3*b^18*c^7+96732*a^3*b^17*c^8-71524*a^3*b^16*c^9+15216*a^3*b^15*c^10-29616*a^3*b^14*c^11+28232*a^3*b^13*c^12+28232*a^3*b^12*c^13-29616*a^3*b^11*c^14+15216*a^3*b^10*c^15-71524*a^3*b^9*c^16+96732*a^3*b^8*c^17-35184*a^3*b^7*c^18-5664*a^3*b^6*c^19-16884*a^3*b^5*c^20+37132*a^3*b^4*c^21-24624*a^3*b^3*c^22+6144*a^3*b^2*c^23+372*a^3*b*c^24-332*a^3*c^25+1018*a^2*b^26-5592*a^2*b^25*c+8484*a^2*b^24*c^2+6144*a^2*b^23*c^3-25210*a^2*b^22*c^4+5320*a^2*b^21*c^5+22574*a^2*b^20*c^6+17120*a^2*b^19*c^7-61448*a^2*b^18*c^8+37048*a^2*b^17*c^9-56534*a^2*b^16*c^10+127264*a^2*b^15*c^11-85492*a^2*b^14*c^12+18608*a^2*b^13*c^13-85492*a^2*b^12*c^14+127264*a^2*b^11*c^15-56534*a^2*b^10*c^16+37048*a^2*b^9*c^17-61448*a^2*b^8*c^18+17120*a^2*b^7*c^19+22574*a^2*b^6*c^20+5320*a^2*b^5*c^21-25210*a^2*b^4*c^22+6144*a^2*b^3*c^23+8484*a^2*b^2*c^24-5592*a^2*b*c^25+1018*a^2*c^26-520*a*b^27+3056*a*b^26*c-5592*a*b^25*c^2+372*a*b^24*c^3+6960*a*b^23*c^4+5192*a*b^22*c^5-25960*a*b^21*c^6+24240*a*b^20*c^7-20460*a*b^19*c^8+27064*a*b^18*c^9-7568*a*b^17*c^10-96*a*b^16*c^11-42752*a*b^15*c^12+36064*a*b^14*c^13+36064*a*b^13*c^14-42752*a*b^12*c^15-96*a*b^11*c^16-7568*a*b^10*c^17+27064*a*b^9*c^18-20460*a*b^8*c^19+24240*a*b^7*c^20-25960*a*b^6*c^21+5192*a*b^5*c^22+6960*a*b^4*c^23+372*a*b^3*c^24-5592*a*b^2*c^25+3056*a*b*c^26-520*a*c^27+86*b^28-520*b^27*c+1018*b^26*c^2-332*b^25*c^3-599*b^24*c^4-2120*b^23*c^5+7772*b^22*c^6-11704*b^21*c^7+14433*b^20*c^8-16028*b^19*c^9+17446*b^18*c^10-28912*b^17*c^11+43296*b^16*c^12-38688*b^15*c^13+29704*b^14*c^14-38688*b^13*c^15+43296*b^12*c^16-28912*b^11*c^17+17446*b^10*c^18-16028*b^9*c^19+14433*b^8*c^20-11704*b^7*c^21+7772*b^6*c^22-2120*b^5*c^23-599*b^4*c^24-332*b^3*c^25+1018*b^2*c^26-520*b*c^27+86*c^28)*JS^4-(2*(a^4-a^3*b-a^3*c+a^2*b*c-a*b^3+a*b^2*c+a*b*c^2-a*c^3+b^4-b^3*c-b*c^3+c^4))*(6*a^26-38*a^25*b-38*a^25*c+79*a^24*b^2+230*a^24*b*c+79*a^24*c^2-23*a^23*b^3-449*a^23*b^2*c-449*a^23*b*c^2-23*a^23*c^3-136*a^22*b^4+73*a^22*b^3*c+735*a^22*b^2*c^2+73*a^22*b*c^3-136*a^22*c^4+195*a^21*b^5+775*a^21*b^4*c+353*a^21*b^3*c^2+353*a^21*b^2*c^3+775*a^21*b*c^4+195*a^21*c^5+18*a^20*b^6-797*a^20*b^5*c-1963*a^20*b^4*c^2-2067*a^20*b^3*c^3-1963*a^20*b^2*c^4-797*a^20*b*c^5+18*a^20*c^6-967*a^19*b^7+273*a^19*b^6*c+765*a^19*b^5*c^2+3209*a^19*b^4*c^3+3209*a^19*b^3*c^4+765*a^19*b^2*c^5+273*a^19*b*c^6-967*a^19*c^7+2925*a^18*b^8+407*a^18*b^7*c+617*a^18*b^6*c^2+205*a^18*b^5*c^3-3305*a^18*b^4*c^4+205*a^18*b^3*c^5+617*a^18*b^2*c^6+407*a^18*b*c^7+2925*a^18*c^8-3582*a^17*b^9-4662*a^17*b^8*c+3771*a^17*b^7*c^2-4619*a^17*b^6*c^3+223*a^17*b^5*c^4+223*a^17*b^4*c^5-4619*a^17*b^3*c^6+3771*a^17*b^2*c^7-4662*a^17*b*c^8-3582*a^17*c^9+894*a^16*b^10+10158*a^16*b^9*c-5727*a^16*b^8*c^2+501*a^16*b^7*c^3+4136*a^16*b^6*c^4-557*a^16*b^5*c^5+4136*a^16*b^4*c^6+501*a^16*b^3*c^7-5727*a^16*b^2*c^8+10158*a^16*b*c^9+894*a^16*c^10+350*a^15*b^11-4790*a^15*b^10*c-4506*a^15*b^9*c^2+7298*a^15*b^8*c^3-5944*a^15*b^7*c^4+1424*a^15*b^6*c^5+1424*a^15*b^5*c^6-5944*a^15*b^4*c^7+7298*a^15*b^3*c^8-4506*a^15*b^2*c^9-4790*a^15*b*c^10+350*a^15*c^11+4406*a^14*b^12-8186*a^14*b^11*c+8600*a^14*b^10*c^2-3134*a^14*b^9*c^3+9540*a^14*b^8*c^4-7776*a^14*b^7*c^5+238*a^14*b^6*c^6-7776*a^14*b^5*c^7+9540*a^14*b^4*c^8-3134*a^14*b^3*c^9+8600*a^14*b^2*c^10-8186*a^14*b*c^11+4406*a^14*c^12-8254*a^13*b^13+7006*a^13*b^12*c+10306*a^13*b^11*c^2-8238*a^13*b^10*c^3-13814*a^13*b^9*c^4+1410*a^13*b^8*c^5+8440*a^13*b^7*c^6+8440*a^13*b^6*c^7+1410*a^13*b^5*c^8-13814*a^13*b^4*c^9-8238*a^13*b^3*c^10+10306*a^13*b^2*c^11+7006*a^13*b*c^12-8254*a^13*c^13+4406*a^12*b^14+7006*a^12*b^13*c-25162*a^12*b^12*c^2+6442*a^12*b^11*c^3+7600*a^12*b^10*c^4+23718*a^12*b^9*c^5-25138*a^12*b^8*c^6+5904*a^12*b^7*c^7-25138*a^12*b^6*c^8+23718*a^12*b^5*c^9+7600*a^12*b^4*c^10+6442*a^12*b^3*c^11-25162*a^12*b^2*c^12+7006*a^12*b*c^13+4406*a^12*c^14+350*a^11*b^15-8186*a^11*b^14*c+10306*a^11*b^13*c^2+6442*a^11*b^12*c^3-642*a^11*b^11*c^4-18810*a^11*b^10*c^5-782*a^11*b^9*c^6+11322*a^11*b^8*c^7+11322*a^11*b^7*c^8-782*a^11*b^6*c^9-18810*a^11*b^5*c^10-642*a^11*b^4*c^11+6442*a^11*b^3*c^12+10306*a^11*b^2*c^13-8186*a^11*b*c^14+350*a^11*c^15+894*a^10*b^16-4790*a^10*b^15*c+8600*a^10*b^14*c^2-8238*a^10*b^13*c^3+7600*a^10*b^12*c^4-18810*a^10*b^11*c^5+30786*a^10*b^10*c^6-15658*a^10*b^9*c^7-768*a^10*b^8*c^8-15658*a^10*b^7*c^9+30786*a^10*b^6*c^10-18810*a^10*b^5*c^11+7600*a^10*b^4*c^12-8238*a^10*b^3*c^13+8600*a^10*b^2*c^14-4790*a^10*b*c^15+894*a^10*c^16-3582*a^9*b^17+10158*a^9*b^16*c-4506*a^9*b^15*c^2-3134*a^9*b^14*c^3-13814*a^9*b^13*c^4+23718*a^9*b^12*c^5-782*a^9*b^11*c^6-15658*a^9*b^10*c^7+7600*a^9*b^9*c^8+7600*a^9*b^8*c^9-15658*a^9*b^7*c^10-782*a^9*b^6*c^11+23718*a^9*b^5*c^12-13814*a^9*b^4*c^13-3134*a^9*b^3*c^14-4506*a^9*b^2*c^15+10158*a^9*b*c^16-3582*a^9*c^17+2925*a^8*b^18-4662*a^8*b^17*c-5727*a^8*b^16*c^2+7298*a^8*b^15*c^3+9540*a^8*b^14*c^4+1410*a^8*b^13*c^5-25138*a^8*b^12*c^6+11322*a^8*b^11*c^7-768*a^8*b^10*c^8+7600*a^8*b^9*c^9-768*a^8*b^8*c^10+11322*a^8*b^7*c^11-25138*a^8*b^6*c^12+1410*a^8*b^5*c^13+9540*a^8*b^4*c^14+7298*a^8*b^3*c^15-5727*a^8*b^2*c^16-4662*a^8*b*c^17+2925*a^8*c^18-967*a^7*b^19+407*a^7*b^18*c+3771*a^7*b^17*c^2+501*a^7*b^16*c^3-5944*a^7*b^15*c^4-7776*a^7*b^14*c^5+8440*a^7*b^13*c^6+5904*a^7*b^12*c^7+11322*a^7*b^11*c^8-15658*a^7*b^10*c^9-15658*a^7*b^9*c^10+11322*a^7*b^8*c^11+5904*a^7*b^7*c^12+8440*a^7*b^6*c^13-7776*a^7*b^5*c^14-5944*a^7*b^4*c^15+501*a^7*b^3*c^16+3771*a^7*b^2*c^17+407*a^7*b*c^18-967*a^7*c^19+18*a^6*b^20+273*a^6*b^19*c+617*a^6*b^18*c^2-4619*a^6*b^17*c^3+4136*a^6*b^16*c^4+1424*a^6*b^15*c^5+238*a^6*b^14*c^6+8440*a^6*b^13*c^7-25138*a^6*b^12*c^8-782*a^6*b^11*c^9+30786*a^6*b^10*c^10-782*a^6*b^9*c^11-25138*a^6*b^8*c^12+8440*a^6*b^7*c^13+238*a^6*b^6*c^14+1424*a^6*b^5*c^15+4136*a^6*b^4*c^16-4619*a^6*b^3*c^17+617*a^6*b^2*c^18+273*a^6*b*c^19+18*a^6*c^20+195*a^5*b^21-797*a^5*b^20*c+765*a^5*b^19*c^2+205*a^5*b^18*c^3+223*a^5*b^17*c^4-557*a^5*b^16*c^5+1424*a^5*b^15*c^6-7776*a^5*b^14*c^7+1410*a^5*b^13*c^8+23718*a^5*b^12*c^9-18810*a^5*b^11*c^10-18810*a^5*b^10*c^11+23718*a^5*b^9*c^12+1410*a^5*b^8*c^13-7776*a^5*b^7*c^14+1424*a^5*b^6*c^15-557*a^5*b^5*c^16+223*a^5*b^4*c^17+205*a^5*b^3*c^18+765*a^5*b^2*c^19-797*a^5*b*c^20+195*a^5*c^21-136*a^4*b^22+775*a^4*b^21*c-1963*a^4*b^20*c^2+3209*a^4*b^19*c^3-3305*a^4*b^18*c^4+223*a^4*b^17*c^5+4136*a^4*b^16*c^6-5944*a^4*b^15*c^7+9540*a^4*b^14*c^8-13814*a^4*b^13*c^9+7600*a^4*b^12*c^10-642*a^4*b^11*c^11+7600*a^4*b^10*c^12-13814*a^4*b^9*c^13+9540*a^4*b^8*c^14-5944*a^4*b^7*c^15+4136*a^4*b^6*c^16+223*a^4*b^5*c^17-3305*a^4*b^4*c^18+3209*a^4*b^3*c^19-1963*a^4*b^2*c^20+775*a^4*b*c^21-136*a^4*c^22-23*a^3*b^23+73*a^3*b^22*c+353*a^3*b^21*c^2-2067*a^3*b^20*c^3+3209*a^3*b^19*c^4+205*a^3*b^18*c^5-4619*a^3*b^17*c^6+501*a^3*b^16*c^7+7298*a^3*b^15*c^8-3134*a^3*b^14*c^9-8238*a^3*b^13*c^10+6442*a^3*b^12*c^11+6442*a^3*b^11*c^12-8238*a^3*b^10*c^13-3134*a^3*b^9*c^14+7298*a^3*b^8*c^15+501*a^3*b^7*c^16-4619*a^3*b^6*c^17+205*a^3*b^5*c^18+3209*a^3*b^4*c^19-2067*a^3*b^3*c^20+353*a^3*b^2*c^21+73*a^3*b*c^22-23*a^3*c^23+79*a^2*b^24-449*a^2*b^23*c+735*a^2*b^22*c^2+353*a^2*b^21*c^3-1963*a^2*b^20*c^4+765*a^2*b^19*c^5+617*a^2*b^18*c^6+3771*a^2*b^17*c^7-5727*a^2*b^16*c^8-4506*a^2*b^15*c^9+8600*a^2*b^14*c^10+10306*a^2*b^13*c^11-25162*a^2*b^12*c^12+10306*a^2*b^11*c^13+8600*a^2*b^10*c^14-4506*a^2*b^9*c^15-5727*a^2*b^8*c^16+3771*a^2*b^7*c^17+617*a^2*b^6*c^18+765*a^2*b^5*c^19-1963*a^2*b^4*c^20+353*a^2*b^3*c^21+735*a^2*b^2*c^22-449*a^2*b*c^23+79*a^2*c^24-38*a*b^25+230*a*b^24*c-449*a*b^23*c^2+73*a*b^22*c^3+775*a*b^21*c^4-797*a*b^20*c^5+273*a*b^19*c^6+407*a*b^18*c^7-4662*a*b^17*c^8+10158*a*b^16*c^9-4790*a*b^15*c^10-8186*a*b^14*c^11+7006*a*b^13*c^12+7006*a*b^12*c^13-8186*a*b^11*c^14-4790*a*b^10*c^15+10158*a*b^9*c^16-4662*a*b^8*c^17+407*a*b^7*c^18+273*a*b^6*c^19-797*a*b^5*c^20+775*a*b^4*c^21+73*a*b^3*c^22-449*a*b^2*c^23+230*a*b*c^24-38*a*c^25+6*b^26-38*b^25*c+79*b^24*c^2-23*b^23*c^3-136*b^22*c^4+195*b^21*c^5+18*b^20*c^6-967*b^19*c^7+2925*b^18*c^8-3582*b^17*c^9+894*b^16*c^10+350*b^15*c^11+4406*b^14*c^12-8254*b^13*c^13+4406*b^12*c^14+350*b^11*c^15+894*b^10*c^16-3582*b^9*c^17+2925*b^8*c^18-967*b^7*c^19+18*b^6*c^20+195*b^5*c^21-136*b^4*c^22-23*b^3*c^23+79*b^2*c^24-38*b*c^25+6*c^26)*JS^2+(a^8-5*a^6*b^2+4*a^6*b*c-5*a^6*c^2+2*a^5*b^3-2*a^5*b^2*c-2*a^5*b*c^2+2*a^5*c^3+8*a^4*b^4-12*a^4*b^3*c+17*a^4*b^2*c^2-12*a^4*b*c^3+8*a^4*c^4-8*a^3*b^5+12*a^3*b^4*c-4*a^3*b^3*c^2-4*a^3*b^2*c^3+12*a^3*b*c^4-8*a^3*c^5+3*a^2*b^6-4*a^2*b^5*c-5*a^2*b^4*c^2+12*a^2*b^3*c^3-5*a^2*b^2*c^4-4*a^2*b*c^5+3*a^2*c^6-2*a*b^7+6*a*b^6*c-6*a*b^5*c^2+2*a*b^4*c^3+2*a*b^3*c^4-6*a*b^2*c^5+6*a*b*c^6-2*a*c^7+b^8-4*b^7*c+5*b^6*c^2-4*b^4*c^4+5*b^2*c^6-4*b*c^7+c^8)*(a^8-4*a^7*b-2*a^7*c+5*a^6*b^2+6*a^6*b*c+3*a^6*c^2-6*a^5*b^2*c-4*a^5*b*c^2-8*a^5*c^3-4*a^4*b^4+2*a^4*b^3*c-5*a^4*b^2*c^2+12*a^4*b*c^3+8*a^4*c^4+2*a^3*b^4*c+12*a^3*b^3*c^2-4*a^3*b^2*c^3-12*a^3*b*c^4+2*a^3*c^5+5*a^2*b^6-6*a^2*b^5*c-5*a^2*b^4*c^2-4*a^2*b^3*c^3+17*a^2*b^2*c^4-2*a^2*b*c^5-5*a^2*c^6-4*a*b^7+6*a*b^6*c-4*a*b^5*c^2+12*a*b^4*c^3-12*a*b^3*c^4-2*a*b^2*c^5+4*a*b*c^6+b^8-2*b^7*c+3*b^6*c^2-8*b^5*c^3+8*b^4*c^4+2*b^3*c^5-5*b^2*c^6+c^8)*(a^8-2*a^7*b-4*a^7*c+3*a^6*b^2+6*a^6*b*c+5*a^6*c^2-8*a^5*b^3-4*a^5*b^2*c-6*a^5*b*c^2+8*a^4*b^4+12*a^4*b^3*c-5*a^4*b^2*c^2+2*a^4*b*c^3-4*a^4*c^4+2*a^3*b^5-12*a^3*b^4*c-4*a^3*b^3*c^2+12*a^3*b^2*c^3+2*a^3*b*c^4-5*a^2*b^6-2*a^2*b^5*c+17*a^2*b^4*c^2-4*a^2*b^3*c^3-5*a^2*b^2*c^4-6*a^2*b*c^5+5*a^2*c^6+4*a*b^6*c-2*a*b^5*c^2-12*a*b^4*c^3+12*a*b^3*c^4-4*a*b^2*c^5+6*a*b*c^6-4*a*c^7+b^8-5*b^6*c^2+2*b^5*c^3+8*b^4*c^4-8*b^3*c^5+3*b^2*c^6-2*b*c^7+c^8)*(a^4-a^3*b-a^3*c+a^2*b*c-a*b^3+a*b^2*c+a*b*c^2-a*c^3+b^4-b^3*c-b*c^3+c^4)^2=0

11. (a^8*b^4+2*a^8*b^2*c^2+a^8*c^4-a^6*b^6-a^6*b^4*c^2-a^6*b^2*c^4-a^6*c^6+a^4*b^8-a^4*b^6*c^2-3*a^4*b^4*c^4-a^4*b^2*c^6+a^4*c^8+2*a^2*b^8*c^2-a^2*b^6*c^4-a^2*b^4*c^6+2*a^2*b^2*c^8+b^8*c^4-b^6*c^6+b^4*c^8)*YS^4+(a^8*b^4*c^2+a^8*b^2*c^4-4*a^6*b^6*c^2-7*a^6*b^4*c^4-4*a^6*b^2*c^6+a^4*b^8*c^2-7*a^4*b^6*c^4-7*a^4*b^4*c^6+a^4*b^2*c^8+a^2*b^8*c^4-4*a^2*b^6*c^6+a^2*b^4*c^8)*YS^2+a^8*b^4*c^4-a^6*b^6*c^4-a^6*b^4*c^6+a^4*b^8*c^4-a^4*b^6*c^6+a^4*b^4*c^8=0

12. (a^4-a^2*b^2-a^2*c^2+b^4-b^2*c^2+c^4)*ST^2-3*a^2*b^2*c^2=0