果树问题讨论:这两个问题等价么？

mathe

比如看第一个例子,其中后面标上~的点表示这个点被变换到无穷远点，也就是说，直线
BEHK被映射成无穷远直线。然后A点作为原点，AB作为x轴,AE作为y轴建立仿射坐标系（也就是两个坐标轴不需要相互垂直，对于每个平面上的点，分别过这个点做坐标轴平行线同坐标轴交点到原点距离就是它的坐标）。由于B,E都是无穷远点，我们可以取AC作为x轴的单位,AF作为y轴的单位。
同样还有D点在x轴，G点在y轴，分别假设他们坐标为(d,0)和(0,g)其中d,g为待定系数。
为方便起见，对于每个点的坐标我采用了射影几何种的齐次坐标，也就是平面上每个点$(x_0,y_0)$的齐次坐标为$(k*x_0,k*y_0,k)$,其中k为任意非0的数(比如这里我基本上采用k=1),而齐次坐标的最大好处可以表示无穷远点（在射影几何中，平行线相交于无穷远点，所有任何多条相互平行的直线相交于同一个无穷远点），而所有斜率为t的直线相交的无穷远点齐次坐标可以表示为$(k,k*t,0)$.
然后对于其他点I,J,K,M分别用未知数表示它们的坐标就可以了。然后代入各条方程。
实际上对于n不是太大的时候，好像每条直线都会经过至少一个无穷远点，从而方程很简单（也就是直线的方向都已经知道了），比如对于直线AHIJ，H是无穷远点，所以我们知道线段AI和AJ的斜率都是kH,A是原点，那么马上可以得出Iy=kH*Ix, Jy=kH*Jx；对于直线BFIL,B是无穷远点(1,0,0),也就是直线FIL同x轴平行，而F的y坐标为1，马上得出Iy=Ly=1

mathe

现在采用上面的思路，证明了13个点最多9条线
使用方法如下:
首先使用计算机穷举关于问题2在n=13时线的数目不少于9的所有情况，得到如下各种:
ABCDAEFGAHIJAKLMBEHKBFILBGJMCEJLCFHMCGIKDEIMDFJKDGHL
ABCDAEFGAHIMBEHJBFKMCELMCGIKDGJMDHKLFIJL
ABCDAELMBFGLBHIMCFJMCHKLDGKMDIJLEFIKEGHJ
ABDEAFGHBIJKCFILCGJMDFKMDHJLEGKLEHIM
ABEFAGHMBIJMCEKMCGILDFLMDGJKEHJLFHIK
ABKLAGHMBIJMCDKMCGILDHJLEFLMEGJKFHIK
ABLMAFGHBIJKCFILCGJMDGKLDHIMEFKMEHJL
ACDEBFGHBIJKCFILCGJMDFKMDHJLEGKLEHIM
ADEFAGHIBDGJBHKLCEIKCFJLDILMEHJMFGKM
ADEFAGHIBDJKBEGLCDHMCIJLEIKMFGJMFHKL
ADJKAELMBFJLBGKMCHKLCIJMDFHMDGILEFIKEGHJ
AEFGAHIJAKLMBEHKBFILBGJMCEJLCFHMCGIKDEIMDFJKDGHL
AEFGAHIMBEHJBFKMCELMCGIKDGJMDHKLFIJL
AELMBFGLBHIMCFJMCHKLDGKMDIJLEFIKEGHJ
AHIJAKLMBCHKBDILBEJMCFJLCGIMDFHMDGJKEFIKEGHL
AKLMBCDKBEFLBGHMCEIMCGJLDFJMDHILEHJKFGIK
BCDEBFGHBIJKCFILCGJMDFKMDHJLEGKLEHIM
其中相邻4个字母代表一条“直线”，其中最少9条“直线”，最多13条“直线”。
然后使用上面思路将某条较好的直线通过射影变换映射成无穷远直线，建立仿射坐标系求解
使用计算机产生Wimaxami可以识别的方程组，分别如下：
solve([1=I_x,1=J_x,K_x=L_x,K_x=M_x,1=I_y,1=L_y,G_y=J_y,G_y=M_y,J_y-0=C_y*(J_x-0),L_y-0=C_y*(L_x-0),0-1=C_y*(1-0),M_y-1=C_y*(M_x-0),0-G_y=C_y*(K_x-0),I_y-G_y=C_y*(I_x-0),I_y-0=D_y*(I_x-0),M_y-0=D_y*(M_x-0),0-1=D_y*(K_x-0),J_y-1=D_y*(J_x-0),G_y-0=D_y*(0-1),L_y-0=D_y*(L_x-1)],[C_y,D_y,G_y,I_x,I_y,J_x,J_y,K_x,L_x,L_y,M_x,M_y])
        A=(0,1,0) B=(1,0,0) C=(1,C_y,0) D=(1,D_y,0) E_x=0 E_y=0 F_x=0 F_y=1 G_x=0 H_x=1 H_y=0 K_y=0
solve([H_y-0=M_y*(H_x-0),I_y-0=M_y*(I_x-0),1=H_x,1=J_x,0-1=M_y*(1-0),L_y-1=M_y*(L_x-0),0-1=K_y*(G_x-0),I_y-1=K_y*(I_x-0),0-D_y=M_y*(G_x-0),J_y-D_y=M_y*(J_x-0),H_y-D_y=K_y*(H_x-0),L_y-D_y=K_y*(L_x-0),I_y=J_y,I_y=L_y],[D_y,G_x,H_x,H_y,I_x,I_y,J_x,J_y,K_y,L_x,L_y,M_y])
        A_x=0 A_y=0 B=(0,1,0) C_x=0 C_y=1 D_x=0 E_x=1 E_y=0 F=(1,0,0) G_y=0 K=(1,K_y,0) M=(1,M_y,0)
solve([1=C_x,1=D_x,J_y-0=F_y*(J_x-0),C_y-0=F_y*(C_x-0),1=C_y,1=K_y,K_y-0=G_y*(K_x-0),D_y-0=G_y*(D_x-0),I_y=D_y,I_y=J_y,0-I_y=F_y*(E_x-0),K_y-I_y=F_y*(K_x-0),0-1=G_y*(E_x-0),J_y-1=G_y*(J_x-0)],[C_x,C_y,D_x,D_y,E_x,F_y,G_y,I_y,J_x,J_y,K_x,K_y])
        A_x=1 A_y=0 B=(0,1,0) E_y=0 F=(1,F_y,0) G=(1,G_y,0) H_x=0 H_y=1 I_x=0 L=(1,0,0) M_x=0 M_y=0
solve([1-0=F_y*(0-1),H_y-0=F_y*(H_x-1),B_x=I_x,B_x=J_x,I_y-L_y=F_y*(I_x-0),C_y-L_y=F_y*(C_x-0),C_y-1=M_y*(C_x-0),J_y-1=M_y*(J_x-0),L_y=J_y,L_y=H_y,H_y-0=M_y*(H_x-0),I_y-0=M_y*(I_x-0)],[B_x,C_x,C_y,F_y,H_x,H_y,I_x,I_y,J_x,J_y,L_y,M_y])
        A_x=1 A_y=0 B_y=0 D=(1,0,0) E_x=0 E_y=0 F=(1,F_y,0) G_x=0 G_y=1 K=(0,1,0) L_x=0 M=(1,M_y,0)
solve([0-1=E_y*(1-0),F_y-1=E_y*(F_x-0),K_y-0=E_y*(K_x-0),C_y-0=E_y*(C_x-0),0-G_y=L_y*(I_x-0),C_y-G_y=L_y*(C_x-0),F_y-0=L_y*(F_x-0),D_y-0=L_y*(D_x-0),G_y=D_y,G_y=K_y,I_x=F_x,I_x=K_x],[C_x,C_y,D_x,D_y,E_y,F_x,F_y,G_y,I_x,K_x,K_y,L_y])
[[C_x=1/4,C_y=-1/4,D_x=-1/2,D_y=-1/2,E_y=-1,F_x=1/2,F_y=1/2,G_y=-1/2,I_x=1/2,K_x=1/2,K_y=-1/2,L_y=1]]
        A_x=0 A_y=1 B_x=1 B_y=0 E=(1,E_y,0) G_x=0 H=(0,1,0) I_y=0 J=(1,0,0) L=(1,L_y,0) M_x=0 M_y=0
solve([D_y-0=K_y*(D_x-0),C_y-0=K_y*(C_x-0),0-1=L_y*(1-0),C_y-1=L_y*(C_x-0),0-H_y=L_y*(J_x-0),D_y-H_y=L_y*(D_x-0),F_y-0=L_y*(F_x-0),E_y-0=L_y*(E_x-0),0-1=K_y*(J_x-0),E_y-1=K_y*(E_x-0),H_y-0=K_y*(0-1),F_y-0=K_y*(F_x-1)],[C_x,C_y,D_x,D_y,E_x,E_y,F_x,F_y,H_y,J_x,K_y,L_y])
        A=(0,1,0) B=(1,0,0) G_x=0 G_y=1 H_x=0 I_x=1 I_y=0 J_y=0 K=(1,K_y,0) L=(1,L_y,0) M_x=0 M_y=0
solve([1-0=F_y*(0-1),H_y-0=F_y*(H_x-1),0-J_y=I_y*(B_x-0),K_y-J_y=I_y*(K_x-0),1=D_y,1=K_y,H_y-0=I_y*(H_x-0),D_y-0=I_y*(D_x-0),K_y-0=F_y*(K_x-0),E_y-0=F_y*(E_x-0),J_y=H_y,J_y=E_y],[B_x,D_x,D_y,E_x,E_y,F_y,H_x,H_y,I_y,J_y,K_x,K_y])
        A_x=1 A_y=0 B_y=0 C=(0,1,0) F=(1,F_y,0) G_x=0 G_y=1 I=(1,I_y,0) J_x=0 L=(1,0,0) M_x=0 M_y=0
solve([B_x=G_x,B_x=H_x,J_y-1=I_y*(J_x-0),B_y-1=I_y*(B_x-0),M_y=J_y,M_y=G_y,H_y-0=L_y*(H_x-0),J_y-0=L_y*(J_x-0),0-1=L_y*(E_x-0),G_y-1=L_y*(G_x-0),0-M_y=I_y*(E_x-0),H_y-M_y=I_y*(H_x-0)],[B_x,B_y,E_x,G_x,G_y,H_x,H_y,I_y,J_x,J_y,L_y,M_y])
        A_x=1 A_y=0 C=(1,0,0) D_x=0 D_y=0 E_y=0 F=(0,1,0) I=(1,I_y,0) K_x=0 K_y=1 L=(1,L_y,0) M_x=0
solve([0-1=H_y*(G_x-0),I_y-1=H_y*(I_x-0),K_y-0=H_y*(K_x-1),L_y-0=H_y*(L_x-1),C_x=I_x,C_x=K_x,F_y=C_y,F_y=L_y,I_y-0=M_y*(I_x-0),L_y-0=M_y*(L_x-0),0-F_y=M_y*(G_x-0),K_y-F_y=M_y*(K_x-0)],[C_x,C_y,F_y,G_x,H_y,I_x,I_y,K_x,K_y,L_x,L_y,M_y])
        A_x=0 A_y=1 B_x=1 B_y=0 D_x=0 D_y=0 E=(0,1,0) F_x=0 G_y=0 H=(1,H_y,0) J=(1,0,0) M=(1,M_y,0)
solve([G_y-1=I_y*(G_x-0),H_y-1=I_y*(H_x-0),1=G_x,1=L_x,C_y-0=M_y*(C_x-0),H_y-0=M_y*(H_x-0),C_y-0=I_y*(C_x-J_x),L_y-0=I_y*(L_x-J_x),0-F_y=M_y*(J_x-0),G_y-F_y=M_y*(G_x-0),F_y=H_y,F_y=L_y],[C_x,C_y,F_y,G_x,G_y,H_x,H_y,I_y,J_x,L_x,L_y,M_y])
        A_x=0 A_y=1 B_x=1 B_y=0 D_x=0 D_y=0 E=(0,1,0) F_x=0 I=(1,I_y,0) J_y=0 K=(1,0,0) M=(1,M_y,0)
solve([M_y-0=K_y*(0-1),G_y-0=K_y*(G_x-1),H_y-0=K_y*(H_x-0),C_y-0=K_y*(C_x-0),M_y=I_y,M_y=C_y,0-M_y=D_y*(F_x-0),H_y-M_y=D_y*(H_x-0),I_y-0=D_y*(I_x-0),G_y-0=D_y*(G_x-0),0-1=K_y*(F_x-0),I_y-1=K_y*(I_x-0),1=G_y,1=H_y],[C_x,C_y,D_y,F_x,G_x,G_y,H_x,H_y,I_x,I_y,K_y,M_y])
        A=(0,1,0) B_x=1 B_y=0 D=(1,D_y,0) E_x=0 E_y=1 F_y=0 J=(1,0,0) K=(1,K_y,0) L_x=0 L_y=0 M_x=0
solve([K_x=L_x,K_x=M_x,1-0=F_y*(0-1),L_y-0=F_y*(L_x-1),J_y-0=G_y*(0-1),M_y-0=G_y*(M_x-1),J_y=C_y,J_y=L_y,C_y-0=F_y*(C_x-0),M_y-0=F_y*(M_x-0),0-1=G_y*(K_x-0),C_y-1=G_y*(C_x-0),1=D_y,1=M_y,0-J_y=F_y*(K_x-0),D_y-J_y=F_y*(D_x-0),D_y-0=G_y*(D_x-0),L_y-0=G_y*(L_x-0)],[C_x,C_y,D_x,D_y,F_y,G_y,J_y,K_x,L_x,L_y,M_x,M_y])
        A=(0,1,0) B_x=1 B_y=0 E=(1,0,0) F=(1,F_y,0) G=(1,G_y,0) H_x=0 H_y=0 I_x=0 I_y=1 J_x=0 K_y=0
solve([1=E_y,1=G_y,H_y-0=J_y*(0-1),E_y-0=J_y*(E_x-1),E_y-0=L_y*(E_x-0),C_y-0=L_y*(C_x-0),K_x=G_x,K_x=C_x,G_y-0=J_y*(G_x-0),D_y-0=J_y*(D_x-0),0-H_y=L_y*(K_x-0),D_y-H_y=L_y*(D_x-0)],[C_x,C_y,D_x,D_y,E_x,E_y,G_x,G_y,H_y,J_y,K_x,L_y])
        A_x=0 A_y=1 B_x=1 B_y=0 F=(1,0,0) H_x=0 I=(0,1,0) J=(1,J_y,0) K_y=0 L=(1,L_y,0) M_x=0 M_y=0
solve([J_y-0=F_y*(J_x-0),C_y-0=F_y*(C_x-0),1=C_y,1=K_y,K_y-0=G_y*(K_x-0),D_y-0=G_y*(D_x-0),I_y=D_y,I_y=J_y,0-I_y=F_y*(E_x-0),K_y-I_y=F_y*(K_x-0),0-1=G_y*(E_x-0),J_y-1=G_y*(J_x-0)],[C_x,C_y,D_x,D_y,E_x,F_y,G_y,I_y,J_x,J_y,K_x,K_y])
        A_x=1 A_y=0 B=(0,1,0) E_y=0 F=(1,F_y,0) G=(1,G_y,0) H_x=0 H_y=1 I_x=0 L=(1,0,0) M_x=0 M_y=0
solve([1-0=I_y*(0-1),D_y-0=I_y*(D_x-1),M_y-0=J_y*(0-1),E_y-0=J_y*(E_x-1),0-1=J_y*(C_x-0),F_y-1=J_y*(F_x-0),0-M_y=I_y*(C_x-0),G_y-M_y=I_y*(G_x-0),M_y=F_y,M_y=D_y,G_y-0=J_y*(G_x-0),D_y-0=J_y*(D_x-0),F_y-0=I_y*(F_x-0),E_y-0=I_y*(E_x-0),1=G_y,1=E_y],[C_x,D_x,D_y,E_x,E_y,F_x,F_y,G_x,G_y,I_y,J_y,M_y])
        A=(0,1,0) B_x=1 B_y=0 C_y=0 H=(1,0,0) I=(1,I_y,0) J=(1,J_y,0) K_x=0 K_y=0 L_x=0 L_y=1 M_x=0
solve([M_x=H_x,M_x=G_x,0-1=C_y*(M_x-0),I_y-1=C_y*(I_x-0),J_y-0=C_y*(J_x-0),G_y-0=C_y*(G_x-0),0-F_y=D_y*(M_x-0),J_y-F_y=D_y*(J_x-0),I_y-0=D_y*(I_x-0),H_y-0=D_y*(H_x-0),1=H_y,1=J_y,F_y=G_y,F_y=I_y],[C_y,D_y,F_y,G_x,G_y,H_x,H_y,I_x,I_y,J_x,J_y,M_x])
        A_x=1 A_y=0 B=(0,1,0) C=(1,C_y,0) D=(1,D_y,0) E_x=0 E_y=1 F_x=0 K=(1,0,0) L_x=0 L_y=0 M_y=0
solve([1=J_x,1=K_x,1=J_y,1=M_y,K_y-0=D_y*(K_x-0),M_y-0=D_y*(M_x-0),0-H_y=D_y*(L_x-0),J_y-H_y=D_y*(J_x-0),0-1=E_y*(L_x-0),K_y-1=E_y*(K_x-0),H_y-0=E_y*(0-1),M_y-0=E_y*(M_x-1)],[A_x,A_y,D_y,E_y,H_y,J_x,J_y,K_x,K_y,L_x,M_x,M_y])
        B=(0,1,0) C=(1,0,0) D=(1,D_y,0) E=(1,E_y,0) F_x=0 F_y=0 G_x=0 G_y=1 H_x=0 I_x=1 I_y=0 L_y=0
然后使用计算机验证，可以非常快得到所有不小于10条直线的情况无解或解是虚数。
而9条直线的情况第一组解是虚数不符合要求。
而第二组情况得到解:
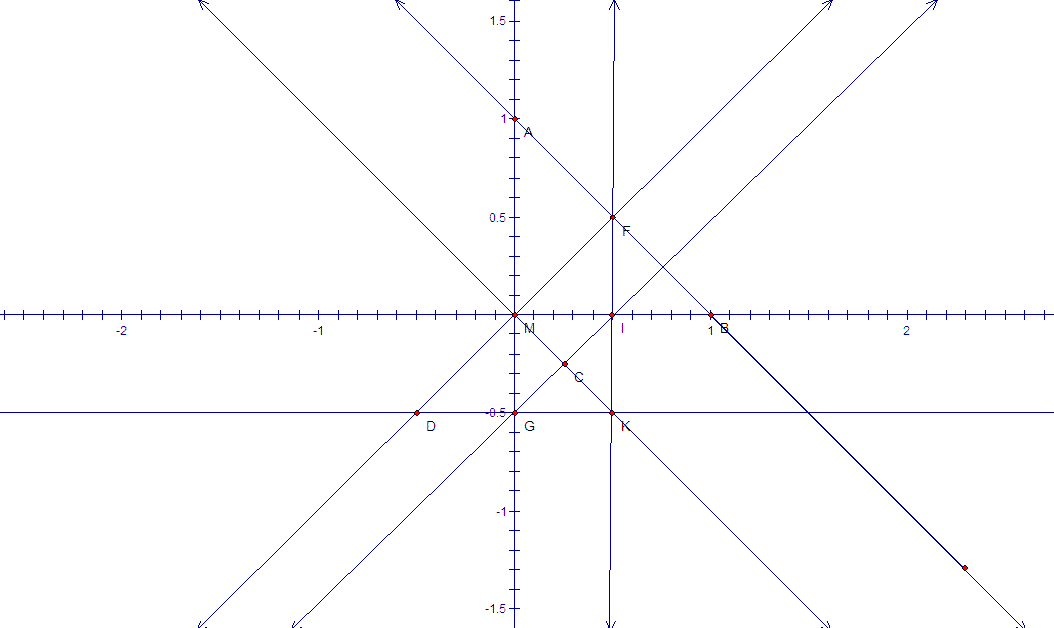
A(0,1)
B(1,0)
C(1/4,-1/4)
D(-1/2,-1/2)
E(1,-1,0)
F(1/2,1/2)
G(0,-1/2)
H(0,1,0)
I(1/2,0)
J(1,0,0)
K(1/2,-1/2)
L(1,1,0)
M(0,0)
对应图如下（需要注意还有一条无穷远直线没有画出来，而所有平行的直线交于无穷远点E,H,I,J也没有画出来）

无心人

呵呵
够乱的了
最大能证明到多少点？

mathe

对于14个点，已经比较麻烦，11条以上直线的问题2组合已经有66种了，让计算机依次验证，全部不合格。
其中59种情况无解，还有一种情况只有虚数解；余下6种情况都有实数解，但是都必然产生5个以上点在同一条直线上（很容易判断，发现解出来一些变量还取0，也就是坐标轴上除了我们事先设定的4个点，还有另外点落在上面）。
所以可以得到14个点情况最多10条直线。wolframe上给出14个点时大于等于10条直线，所以我们可以得到14个点的情况结果就是10。附件中给出上面计算过程。s14是通过计算机产生的关于问题2所有11条以上不等价"直线"情况。s14.solve2是计算机产生的WxMaxima求解表达式和对应的结果
s14.tar.gz (6.61 KB, 下载次数: 7)

2008-8-13 17:02 上传

点击文件名下载附件

无心人

也就是说验证20个点的24条直线的情况
恐怕是目前所无法完成的了？

无心人

我想应该存在20点的24直线解

mathe

不过14个点10条直线情况的问题2对应解已经有186组了，我检验了前面10来组都不行（而且其中不过14个点10条直线情况的问题2对应解已经有186组了，我检验了前面10来组都不行（而且其中有一组计算机求解失败）。而完全检验好像有点太繁琐了。附件中给出了所有10条直线的情况，大家看看能否利用它们找出一个14点10条直线的解。
l10.tar.gz (12.03 KB, 下载次数: 3)

2008-8-13 18:09 上传

点击文件名下载附件

mathe

需要解决如何有效的进行符号运算求解的问题。

mathe

还有通过这种方法，20个点超过14条直线的问题2的解的数目估计会非常非常之多，可能很难一一处理

无心人

应该找一个筛选的条件
使得能筛选掉一些不符合几何规律的
问题2的解