点到三角形三边中点距离之和与到三个顶点距离之和的比值

lsr314

记点$P$到三角形$ABC$三边中点的距离之和为$m$，到三个顶点距离之和为$n$，问$m/n>1/3$是否恒成立?
点$P$在直角三角形斜边中点, 一个角趋近于0的时候，比值可以无限接近$1/3$.

mathematica

估计没最小值！

dlpg070

m/n>1/3恒成立
如果P点在三角形的重心,与三角形形状无关,永远m/n=0.5
其他情形P点在AB中点D 或P点在AC中点E都是的m/n取较小值,但恒>1/3
我在三角形内外做了几十个样点,没发现例外
求最小值应该可行
给出几个图例

lsr314

这道题已经有人用复数法证明了。

wayne

我比较好奇的是，给定一个三角形，使得比值最小的点 是什么点，比值最小又是多少。

数学星空

对于直角三角形的斜边上的中点P,三边长分别为\(a,b,c\),且设\(a\leq b,c^2=a^2+b^2\)
有\(m=\frac{a+b}{2}\),\(n=\frac{3\sqrt{a^2+b^2}}{2}\)
则有\(\frac{1}{3}\lt\frac{m}{n}\leq\frac{\sqrt{2}}{3}\)

王守恩

dlpg070 发表于 2020-9-10 19:26
m/n>1/3恒成立
如果P点在三角形的重心,与三角形形状无关,永远m/n=0.5
其他情形P点在AB中点D 或P点在AC中 ...

   记A≤B≤C，  即：A≤60°，B<90°

\(\D BC=a=\sin A\ \ \ CA=b=\sin B\ \ \ AB=c=\sin(A+B)\)

求：\(\D\frac{m}{n}=\frac{PE+PD}{PA+PB+PC}=\frac{PE+PD}{AB+PC}\)

\(\D=\frac{\frac{\sin A}{2}+\frac{\sin B}{2}}{\sin(A+B)+\frac{1}{2}\sqrt{2\sin^2A+2\sin^2B-\sin^2(A+B)}}\) 的最小值。

dlpg070

王守恩 发表于 2020-9-11 03:22
记A≤B≤C，  即：A≤60°，B

经分析,你的公式在给定条件下是正确的
你的给定条件是:  AB中点F , BC中点D, CA中点E ,P点在AB的中点F
因为P点固定在F点,所以公式是特例,所求最小值没有普遍意义
P应在平面内,题目没有说P在三角形内

dlpg070

王守恩 发表于 2020-9-11 03:22
记A≤B≤C，  即：A≤60°，B

经分析,你的公式在给定条件下是正确的
你的给定条件是:  AB中点F , BC中点D, CA中点E ,P点在AB的中点F
因为P点固定在F点,所以公式是特例,所求最小值没有普遍意义
P应在平面内,题目没有说P在三角形内

数学星空

设三角形三个顶点\(A[x_1,y_1],B[x_2,y_2],C[x_3,y_3]\),三条边\(BC,AC,AB\)上三个点\(D[x_4,y_4],E[x_5,y_5],F[x_6,y_6]\),三角形内点\(P[x,y]\)

我们设最长边位于x轴上\(c\leq b\leq a\), B位于原点，C位于x正半轴上,且\(\frac{BD}{DC}=k_1,\frac{CE}{EA}=k_2,\frac{AF}{FB}=k_3\)

则有：\(x_2=0,y_2=0,x_3=a,y_3=0,x_1=\frac{a^2-b^2+c^2}{2a},y_1=\frac{2s}{a},x_4=\frac{k_1a}{1+k_1},y_4=0,x_5=\frac{k_2(a^2-b^2+c^2)+2a^2}{2a(1+k_2)},y_5=\frac{2sk_2}{a(1+k_2)},x_6=\frac{a^2-b^2+c^2}{2a(1+k_3)},y_6=\frac{2s}{a(1+k_3)},16s^2=2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4\)

\(L=\frac{AP+BP+CP}{DP+EP+FP}=\frac{\sqrt{(x-x_1)^2+(y-y_1)^2}+\sqrt{(x-x_2)^2+(y-y_2)^2}+\sqrt{(x-x_3)^2+(y-y_3)^2}}{\sqrt{(x-x_4)^2+(y-y_4)^2}+\sqrt{(x-x_5)^2+(y-y_5)^2}+\sqrt{(x-x_6)^2+(y-y_6)^2}}\)

\(L\)取极值条件为：分别对上式分别对x,y求导得到：

\(\frac{\sin(\alpha_1)+\sin(\alpha_2)+\sin(\alpha_3)}{\sin(\beta_1)+\sin(\beta_2)+\sin(\beta_3)}=\frac{\cos(\alpha_1)+\cos(\alpha_2)+\cos(\alpha_3)}{\cos(\beta_1)+\cos(\beta_2)+\cos(\beta_3)}=\frac{\sqrt{(x-x_1)^2+(y-y_1)^2}+\sqrt{(x-x_2)^2+(y-y_2)^2}+\sqrt{(x-x_3)^2+(y-y_3)^2}}{\sqrt{(x-x_4)^2+(y-y_4)^2}+\sqrt{(x-x_5)^2+(y-y_5)^2}+\sqrt{(x-x_6)^2+(y-y_6)^2}}\)

上式中

\(\cos(\alpha_1)=\frac{x-x_1}{\sqrt{(x-x_1)^2+(y-y_1)^2}},\sin(\alpha_1)=\frac{y-y_1}{\sqrt{(x-x_1)^2+(y-y_1)^2}}\)
\(\cos(\alpha_2)=\frac{x-x_2}{\sqrt{(x-x_2)^2+(y-y_2)^2}},\sin(\alpha_2)=\frac{y-y_2}{\sqrt{(x-x_2)^2+(y-y_2)^2}}\)
\(\cos(\alpha_3)=\frac{x-x_3}{\sqrt{(x-x_3)^2+(y-y_3)^2}},\sin(\alpha_3)=\frac{y-y_3}{\sqrt{(x-x_3)^2+(y-y_3)^2}}\)
\(\cos(\beta_1)=\frac{x-x_4}{\sqrt{(x-x_4)^2+(y-y_4)^2}},\sin(\beta_1)=\frac{y-y_4}{\sqrt{(x-x_4)^2+(y-y_4)^2}}\)
\(\cos(\beta_2)=\frac{x-x_5}{\sqrt{(x-x_5)^2+(y-y_5)^2}},\sin(\beta_2)=\frac{y-y_5}{\sqrt{(x-x_5)^2+(y-y_5)^2}}\)
\(\cos(\beta_3)=\frac{x-x_6}{\sqrt{(x-x_6)^2+(y-y_6)^2}},\sin(\beta_3)=\frac{y-y_6}{\sqrt{(x-x_6)^2+(y-y_6)^2}}\)

例如取：

\({a = 5, b = 4, c = 3, k_1 = 1, k_2 = 2, k_3 = 1}\)

得到：

\(L=\frac{\sqrt{(x-\frac{5}{2})^2+y^2}+\sqrt{(x-\frac{43}{15})^2+(y-\frac{8}{5})^2}+\sqrt{(x-\frac{9}{10})^2+(y-\frac{6}{5})^2}}{\sqrt{x^2+y^2}+\sqrt{(x-5)^2+y^2}+\sqrt{(x-\frac{9}{5})^2+(y-\frac{12}{5})^2}}\)

计算得到极值点\(x=0.9,y=1.2\)

画图得到：
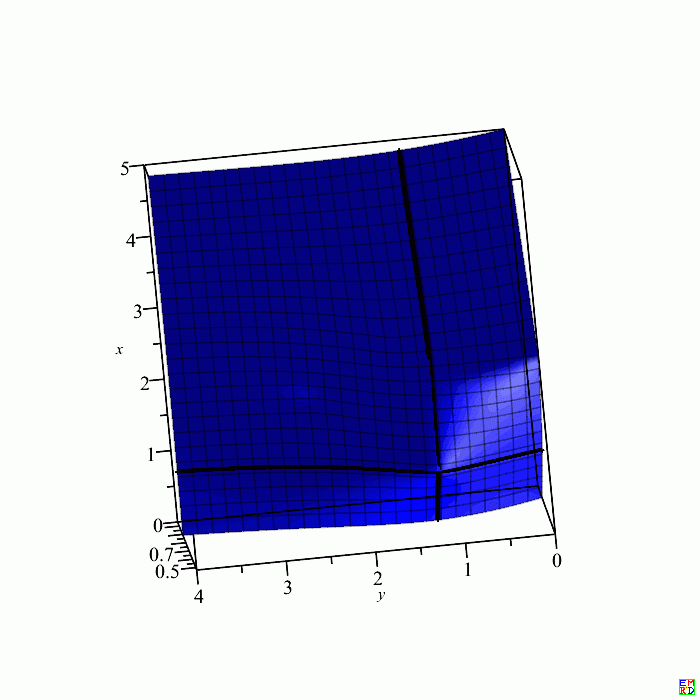