点到三角形三边中点距离之和与到三个顶点距离之和的比值

dlpg070

数学星空 发表于 2020-9-14 22:46
设三角形三个顶点\(A[x_1,y_1],B[x_2,y_2],C[x_3,y_3]\),三条边\(BC,AC,AB\)上三个点\(D[x_4,y_4],E[x_5,y_ ...

实例数据:
a = 5; b = 4; c = 3; k1 = 1; k2 = 2; k3 = 1;
L= ((Sqrt[(-(43/15)+x)^2+(-(8/5)+y)^2]+Sqrt[(-(5/2)+x)^2+y^2]+Sqrt[-50 x+2 (7 x-24 y)+5 (9+4 (x^2+y^2))]/(2 Sqrt[5]))/(Sqrt[(5-x)^2+y^2]+Sqrt[x^2+y^2]+Sqrt[9-(18 x)/5+x^2-(24 y)/5+y^2]))
验算结果表明:
1 全部给出的公式正确(偏导求极值没有给出公式和代码)
2 但是实例计算极值可能有误? 参看图片
  P(0.9,1.2)实际是F点 ,由下列测试数据,显然不是极小值点,可能是误入局部小坑

P=D {5/2,0}     L=0.48553
P=E {43/15,8/5} L=0.500952
P=H {59/20,3/5} L=0.534091
P=F {9/10,6/5}  L=0.551008

图形文件(k2=2)
3顶点3中点_数学星空k2_36.8699度_0.551008-20200915.png

dlpg070

dlpg070 发表于 2020-9-16 09:06
实例数据:
a = 5; b = 4; c = 3; k1 = 1; k2 = 2; k3 = 1;
L= ((Sqrt[(-(43/15)+x)^2+(-(8/5)+y)^2]+S ...

修改的实例1(符合原题要求)
a = 5; b = 4; c = 3; k1 = 1; k2 = 1; k3 = 1;
试图用解方程Solve或用Minimize函数求解极值没有成功,请求帮助
用瞎子登山笨法子得:
极值点在最长边的中点,D点
P=D {5/2,0}     L=0.466667
P=E {17/5,6/5}  L=0.525932
P=H {59/20,3/5} L=0.499286
P=F {9/10,6/5}  L=0.618812


3顶点3中点_数学星空k1_36.8699度_0.466667-20200915.png

mathe

如图，$m+n+h\gt a$
同理$m+n+h \gt b$, $m+n+h \gt c$
所以$\frac{m+n+h}{a+b+c} \gt \frac{1}{3}$
而接近极限时，必然$a=b=c$也就是P是$\Delta ABC$的外心，而且这时a,b,c三条原始线段应该接近平行，也就是B和C无穷接近的情况

dlpg070

mathe 发表于 2020-9-16 10:54
如图，$m+n+h\gt a$
同理$m+n+h \gt b$, $m+n+h \gt c$
所以$\frac{m+n+h}{a+b+c} \gt \frac{1}{3}$

为验证,做了2个例子
结果如下,供参考,如有错误请批评:
例1:
三角形 :A=20° s=10 C=40°
P=D {8.48733,1.26928}  L=0.695166
P=E {5,0}              L=0.430216(最长边中心点)
P=H {4.24366,0.634642} L=0.467184
P=F {3.48733,1.26928}  L=0.496153
P=O1 {5,-2.88675}      L=0.735246(外心)
除特殊情形外,外心不是最小值点,通常L值较大
图形文件名:
3顶点3中点_mathe例1_20.度_0.430216-20200916.png
--------------------
例2:小角度
三角形 :A=2° s=10 C=40°

P=D {9.80023,0.167628}  L=0.949621
P=E {5,0}               L=0.346545 (最长边中心点)
P=H {4.90011,0.0838138} L=0.350928
P=F {4.80023,0.167628}  L=0.355247
P=O1 {5,-5.55306}       L=0.836193 (外心)
除特殊情形外,A为小角度时,外心不是最小值点,通常L值较大
图形文件名:
3顶点3中点_mathe例1_2.度_0.346545-20200916.png

mathe

只是在全局最优时(接近1/3)时P点趋向外心，但是不代表每个三角形都是外心最优

mathe

这道题目固定三角形ABC求P使得题目中比值求最小值挺困难的。
但是如果我们固定PA,PB,PC的长度，但是三者可以自由绕P点旋转，这时求题目中比值的最小值就不难了。
假设$PA \ge PB, PA\ge PC$,那么当B和C都移动到PA的方向延长线上,比值可以取到最小值。

如上图，B和C很接近PA的方向延长线时，2m+2n+2h就会几乎和2a重叠，从而$\frac{m+n+h}{a+b+c}$趋向下界$\frac{a}{a+b+c}$

dlpg070

例9最小值点是外心

m/n最小值公式:已初步验证

约定:用角边角格式表示三角形,aA<=aC<=aB,P={x,y}
O:重心,O1:外心,E:最长边的中点(AC的中点)
如果P点在三角形的重心,与三角形形状无关,永远L=m/n=0.5
如果是钝角三角形 P在最长边中心,L=m/n最小
如果是直角角三角形 P在最长边中心=外心,L=m/n最小
如果是锐角三角形,P在外心,L=m/n最小

即:最小值点永远在E 或 O1点

计算L=m/n的公式:
fL[x_, y_] := (Sqrt[(-(s/2) + x)^2 +
       y^2] + \[Sqrt]((x -
           1/2 s Cos[aA] Csc[aA + aC] Sin[aC])^2 + (y -
           1/2 s Csc[aA + aC] Sin[aA] Sin[aC])^2) + \[Sqrt](1/
          4 (s - 2 x + s Cos[aA] Csc[aA + aC] Sin[aC])^2 + (y -
           1/2 s Csc[aA + aC] Sin[aA] Sin[aC])^2))/(Sqrt[(s - x)^2 +
       y^2] + Sqrt[x^2 + y^2] +
     Sqrt[(x - s Cos[aA] Csc[aA + aC] Sin[aC])^2 + (y -
          s Csc[aA + aC] Sin[aA] Sin[aC])^2]);
         
计算最小值点公式:
fP[aA_,s_,aC_]:=
  If[(aA+aC)>Pi/2],{s/2,1/2 (-s Cot[aA]+s Cos[aA] Cot[aA] Csc[aA+aC] Sin[aC]+s Csc[aA+aC] Sin[aA] Sin[aC])},{s/2,0}]
  

-----------------
计算实例:共设计12个,选录3个

例 1:20.度_10_40.度_例1一般三角形aA<=60度,aC>=aA
P=D {8.48733,1.26928}  L=0.695166
P=E {5,0}              L=0.430216 (最长边中心点 最小值点)
P=H {4.24366,0.634642} L=0.467184
P=F {3.48733,1.26928}  L=0.496153
P=O {5.65822,0.846189} L=0.5
P=O1 {5,-2.88675}      L=0.735246 (外心)
按公式计算结果:正确
最小值点= {5,0} L=m/n最小值= 0.430216
-----------------------
例 2:2.度_10_40.度_例2一般三角形aA小角,aC>=aA
P=D {9.80023,0.167628}  L=0.949621
P=E {5,0}               L=0.346545(最长边中心点 最小值点)
P=H {4.90011,0.0838138} L=0.350928
P=F {4.80023,0.167628}  L=0.355247
P=O {6.53349,0.111752}  L=0.5
P=O1 {5,-5.55306}       L=0.836193(外心)
按公式计算结果:正确
最小值点= {5,0} L=m/n最小值= 0.346545
----------------------
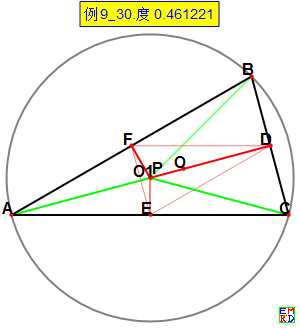
例 9:30.度_10_75.度_例9等腰三角形AB=AC
P=D {9.33013,2.5}     L=0.674053
P=E {5,0}             L=0.468506(最长边中心点)
P=H {4.66506,1.25}    L=0.469825
P=F {4.33013,2.5}     L=0.468506
P=O {6.22008,1.66667} L=0.5
P=O1 {5,1.33975}      L=0.461221(外心 最小值点)
按公式计算结果:正确
最小值点= {5,1.33975} L=m/n最小值= 0.461221

-------------------------
图片是例9的图形,最小值点是外心,不需要A趋于0,也不是趋于外心

数学星空

我们换一种平面几何的计算来演算一下：

设三角形\(ABC\)的内点P及\(BC,AC,AB\)边上的中点\(D,E,F\)，且

\(PA=x,PB=y,PC=z, PD=x_1,PE=y_1,PF=z_1\), 三边长及面积分别为\(a,b,c,s, \angle BPC=\alpha,\angle APC=\beta,\angle APB=\gamma\)

为输入方便记：

\(x_1=\sqrt{2(y^2+z^2)-a^2}\)

\(y_1=\sqrt{2(x^2+z^2)-b^2}\)

\(z_1=\sqrt{2(x^2+y^2)-c^2}\)

且有：

\(2s=yz\sin(\alpha)+xz\sin(\beta)+xy\sin(\gamma)\)

\(k=\frac{PD+PE+PF}{PA+PB+PC}=\frac{x_1+y_1+z_1}{2(x+y+z)}\)  (1)

对下式利用拉格朗日乘子法

\(\frac{x_1+y_1+z_1}{2(x+y+z)}-t(yz\sin(\alpha)+xz\sin(\beta)+xy\sin(\gamma)-2s)\)

得到：

\(4x(\frac{1}{y_1}+\frac{1}{z_1})(x+y+z)-(x_1+y_1+z_1)=2t(x+y+z)^2(y\sin(\gamma)+z\sin(\beta))\)

\(4y(\frac{1}{x_1}+\frac{1}{z_1})(x+y+z)-(x_1+y_1+z_1)=2t(x+y+z)^2(x\sin(\gamma)+z\sin(\alpha))\)

\(4z(\frac{1}{x_1}+\frac{1}{y_1})(x+y+z)-(x_1+y_1+z_1)=2t(x+y+z)^2(x\sin(\beta)+y\sin(\alpha))\)

然后对上面三式分别乘以\(x,y,z\)并相加可以得到：

\(4(x^2+y^2+z^2)(\frac{1}{x_1}+\frac{1}{y_1}+\frac{1}{z_1})-4(\frac{x^2}{x_1}+\frac{y^2}{y_1}+\frac{z^2}{z_1})=8ts(x+y+z)+(x_1+y_1+z_1)\)

我们利用（1）及

\((-a^2 + y^2 + z^2)^2x^2 + (-b^2 + x^2 + z^2)^2y^2 + (-c^2 + x^2 + y^2)^2z^2 - (-a^2 + y^2 + z^2)(-b^2 + x^2 + z^2)(-c^2 + x^2 + y^2) - 4x^2y^2z^2=0\)

可以方便的消元得到\(x,y,k\)的代数方程(这步较容易）

然后分别对\(x,y\)求导，可以求得取极值时\(x,y\)的代数方程（表达式太大，消元工作超出了我的计算机能力）

lsr314

试了几个例子，即使是直角三角形的时候，$P$一般也不是外心，只是有时离外心很近。
例如，当直角三角形的直角边$a=5,b=1$时，外心为斜边中点，坐标为$(x,y)=(5/2,1/2)$,对应的比值为$sqrt(2/13)=0.392232$
而当$x=2.42799,y=0.342129$时，对应的比值为$0.390927$.
锐角三角形也一样，就不举例了。

mathe

只是比较接近外心，但是应该不是外心。
通过GeoGebra做图，取A(-2.88,2.66), B(-5.06,-0.7), C(0.88.-0.74),各边中点D,E,F.
做图得到外心O坐标(-2.0867801412779,-0.2418509797661)

然后放大图片，并移动P尽量和外心O重叠时得到比例约为0.4812647264551

将P向左偏小移动，比如P(-2.1160412915557,-0.3017366751079)时
得到比例为0.4810946700579

所以显然外心不是比例最小的时候