火车站的最佳位置

KeyTo9_Fans

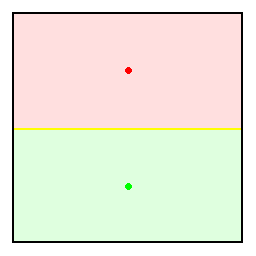
经过随机撒点试验，答案确实会收敛到$18#$的方案去。 代码如下：

1. #include<cstdio>
2. #include<cstdlib>
3. #include<cmath>
5. double xa,ya,xb,yb,tmp,min;
7. double f() //计算平均距离
8. {
9. double x,y,a,b,s;
10. s=0;
11. for(x=1e-4;x<1;x+=2e-3)
12. for(y=1e-4;y<1;y+=2e-3)
13. {
14. a=(x-xa)*(x-xa)+(y-ya)*(y-ya);
15. b=(x-xb)*(x-xb)+(y-yb)*(y-yb);
16. if(a<b)s+=sqrt(a);
17. else s+=sqrt(b);
18. }
19. return s/25e4;
20. }
22. int main()
23. {
24. min=1e9;
25. while(1) //死循环，不断地随机撒点试验
26. {
27. xa=rand()/32768.0;
28. ya=rand()/32768.0;
29. xb=1-xa;
30. yb=1-ya;
31. tmp=f(); //计算平均距离
32. if(tmp<min) //与最优结果比较
33. {
34. min=tmp; //更新最优结果
35. printf("(%lf,%lf),(%lf,%lf): %lf\n",xa,ya,xb,yb,min); //输出当前的最优结果
36. }
37. }
38. return 0;
39. }

复制代码

输出如下：

1. (0.001251,0.563568),(0.998749,0.436432): 0.384276
2. (0.193298,0.808716),(0.806702,0.191284): 0.346670
3. (0.584991,0.479858),(0.415009,0.520142): 0.334438
4. (0.822815,0.746582),(0.177185,0.253418): 0.333470
5. (0.710480,0.513519),(0.289520,0.486481): 0.298872
6. (0.462067,0.235321),(0.537933,0.764679): 0.297309
7. (0.743713,0.468445),(0.256287,0.531555): 0.296855
8. (0.747314,0.496887),(0.252686,0.503113): 0.296630
9. (0.247711,0.497955),(0.752289,0.502045): 0.296626
10. (0.505096,0.749603),(0.494904,0.250397): 0.296623
11. (0.502930,0.250977),(0.497070,0.749023): 0.296621
12. (0.500458,0.750427),(0.499542,0.249573): 0.296618

复制代码

所以$19#$的疑问已经解开： $1$. 把车站设在两个等腰三角形的$Fans$心上，答案不优，为$0.301221$。 $2$. 将正方形分成两个直角梯形，分别找这两个直角梯形的$Fans$心，那么当这两个直角梯形退化成矩形时，答案最优，为$0.29662$。 如下图所示：

056254628

楼上是对吧，关于对角线对称时，确实不是三等分点。 在对角线上，一个火车站距边的距离约等于0.324432，才取最小值0.301226609674926. 当时因只取到小数点后2位，得到0.32值，想当然的认为是0.3333..... 犯了大错误。

056254628

21楼的方法：将正方形分成两个直角梯形，分别找这两个直角梯形的Fans心。 是有问题的。 有时两个火车站点不能同时取到各自图形的Fans心。 因为两个相邻图形的分界线必须垂直平分两个火车点的连线

056254628

三个火车站点A、B、C 构成一个三角形。 三条边的三条垂直平分线相交于外心O. 与城市的边界分别交与A‘，B’，C’。 OA',OB',OC'把城市分成3个部分，每个部分都有自己内部的一个站点。 那么可以分别计算每个部分到各自火车站点的平均距离Da，Db，Dc 和各自图形的面积Sa，Sb，Sc。 其中 Sa+Sb+Sc=1 那么总的平均距离d=Sa*Da+Sb*Db+Sc*Dc

KeyTo9_Fans

上面几层楼的想法都很有道理。 猜想： 当$N$是完全平方数时，$N$个火车站的排列是有规律的。 规律如下： 将大正方形分成$n$*$n$个小正方形，其中$n$*$n$=$N$。 这$N$个火车站就分别位于$n$*$n$个小正方形的中心。 平均距离为$1/(6n)*(\sqrt(2)+ln(1+\sqrt(2)))$。

mathe

对于一个简单凸图形的"Fans心",发现它好像很简单，还是重心，只是不是通常意义上的重心，而是边界的重心。也就是说如果用均匀铁丝围成一个简单凸凸形，其"Fans心"就应该是铁丝的重心

jiaon

这个问题是不是等价于求3个圆把正方形完全覆盖，3个圆中最大的那个半径尽量小。

zgg___

对于一个简单凸图形的"Fans心",发现它好像很简单，还是重心，只是不是通常意义上的重心，而是边界的重心。也就是说如果用均匀铁丝围成一个简单凸凸形，其"Fans心"就应该是铁丝的重心 mathe 发表于 2010-11-7 06:55

如果真的是这样子的，就太神奇了，呵呵。 这是为什么呢？mathe是怎么发现的呢？

mathe

由于“Fans心”是到一个平面区域内所有点平均距离最小的点，我们可以先将这个平面区域离散化，假设离散化以后是n个点$(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$ 那么一个点$(x,y)$到这n个点的距离之和为 $\sum_{t=1}^nsqrt((x-x_i)^2+(y-y_i)^2)$ 我们要求这个和式最小，分别对x,y求偏导得到取最小值的条件为 ${(\sum_{t=1}^n{x-x_i}/{sqrt((x-x_i)^2+(y-y_i)^2)}=0),(\sum_{t=1}^n{y-y_i}/{sqrt((x-x_i)^2+(y-y_i)^2)}=0):}$ 于是如果我们取充分多的点，那么得到Fans心的坐标$(x_0,y_0)$满足积分式 ${(\int_D{x_0-x}/{sqrt((x_0-x)^2+(y_0-y)^2)}dxdy=0),(\int_D{y_0-y}/{sqrt((x_0-x)^2+(y_0-y)^2)}dxdy=0):}$ 如果我们以Fans心$(x_0,y_0)$为原点，建立极坐标，设$r=(x,y)$是有向向量,$\theta$是对应向量的角度，而对于每个角度，最大长度向量为$R(\theta)$那么上面表达式就是 $\int_D r/{|r|}dxdy=0$ 由于$dxdy=|r|d|r|d\theta$,我们可以将上面表达式转化为: $\int_{\theta=0}^{2pi}\int_{h=0}^{|R(\theta)|}rd|r|d\theta=0$ 我们知道对于固定的$\theta$,$r/{|r|}=R/{|R|}$(因为它们都代表这个方向的单位向量) 所以上面积分等于 $\int_{\theta=0}^{2pi}R/{|R|}d\theta\int_{h=0}^{|R(\theta)|}|r|d|r|=0$ 即$1/2\int_{\theta=0}^{2pi}R(\theta)|R(\theta)|d\theta=0$ 而对于边界$\delta D$,$|R(\theta)|d\theta=ds$,其中$s$代表边界的弧长，所以上面积分等于 $\int_{\delta D}Rds=0$ 或者也可以写成 ${(\int_{\delta D}xds=0),(\int_{\delta D}yds=0):}$ 也就是我们要求任何方向的最大向量（对应边界上的点）沿着边界曲线积分为0 也就是边界上所有点的坐标本身的曲线积分为原点，也就是原点（即Fans心）就是边界的重心。

hujunhua

mathe对Fans心的定性使我想起了高中时的数学老师讲的古鲁金(P.Guldin)定理的事情。 【古鲁金(P.Guldin)定理】平面图形绕与它不相交的定直线旋转而生成的旋转体的体积等于其面积与重心所画出的圆周长的乘积． 这个用来计算旋转体的体积显然是极其便捷的。高中本来是不学这个定理的，一般的数学老师也不知道。但我们高中的那个老师是大学的数学教授，当年被划为“牛鬼蛇神”下放改造时留在中学的，常跟我们讲些大学的东西。我高中就学完大学的高数也是他老人家拔苗助长的结果，“害”我大学的数学课没去上过几节期末考试60几分（记得在某个帖子里讲过这个糗事）。言归正传，老师出了一个三角形绕形外一条直线旋转，求旋转体体积和表面积的题。对比了两种计算方法，一个是分解为若干个锥台，另一个是用古鲁金定理。但是在计算表面积时两种方法的结果不一致，也就是用三角形重心所划的圆周长乘以三角形周长的结果与三个锥台的侧面积之和不相等。老师觉得不可思议，反复验算了几次，最后不得不说：古鲁金定理不包括旋转体的表面积计算。 我那时对这个定理很着迷，因为它效率高啊，觉得面积计算应该也有类似的方法，老师的想法是有道理的。于是试着计算了一下用三角形的边界重心所划的周长与三角形周长的乘积，果然相符，告诉老师后被狠狠表扬的一下，我对数学的兴趣就是这样被这位拔苗师一点点助长起来的。为了计算这道题，偶那时才发现三角形的边界重心是它的中点三角形的内心。