火车站的最佳位置

mathe

对于正方形内部三个火车站，那么根据对称性，可以猜测最优结果是下面三种之一: 其中第一种很简单，分割点都是三等分点。 第二个中间图形的Fans心就是正方形中心，而两边的Fans心是等腰直角三角形的Fans心，在根据两个Fans心关于分割线对称，可以非常容易计算出Fans心的坐标$(1/{4-sqrt(2)},1-1/{4-sqrt(2)})$ 但是第三个图形比较复杂，求解析解很难，但是通过数值计算可以得出3条分割线的交点坐标为 $(0.508163061658346268646554069976,0.508163061658346268646554069976)$ 而分割线同边的交点坐标为$(0,0.669356244688383322873772827933)$ 于是Fans心坐标为$(0.279986122929630824786523085934,0.279986122929630824786523085934)$ 和$(0.453231593602525618908990293995,0.826144137435582230878607355688)$ 有了这些信息，我们就可以计算出三种情况平均距离，取最小的就可以了。直观的看，应该第三种结果最优，第一种结果最差

mathe

模拟计算一下，第三种最好，平均距离为0.239,第二种最差，为0.306,而第一种为0.274 所以对于三个火车站，最优平均距离应该为0.239

KeyTo9_Fans

这种方案如何？

mathe

对的，我遗漏了这个方案，其中三个分割线交点坐标为(0.5,0.518207225941510822787332148797) 而分割线和边界交点为(0,0.774766575572345591507339519541) Fans心的坐标为(0.25,0.338738712728079676957958677813),(0.5,0.825955413970359352976709305153) 模拟计算平均距离为0.2366,比上面的方案要略好，而且这种方案应该还可以适用于矩形

mathe

发现我的结论是错误的， 原因在于我使用了一个错误的结论 在29#我认为$|R|d\theta=ds$,可是实际上这个结论不成立

056254628

mathe的方法都是建立在分图形的Fans心刚好都是关于分界垂直平分。这样的结果是不是能算出最小值，没有被证明。 我的思路，任意设定三个站点的坐标，利用解析方法计算出垂直平分线及图形的分界，计算每个图形的平均距离。对三个分图形的平均距离再进行平均。而权重系数就是图形的面积。 可以采用我在14楼所说的总平均距离的计算公式。 --------------------------------------------------------------------- 计算图形的平均距离，有精确公式。可以大大减少计算它所花的时间。 可以把目标点与图形的所有顶点相连，这样就把图形分成了若干个三角形的组合。 我们只要有了计算三角形对其顶点的平均距离的计算公式，就可计算所有图形的计算公式。为了计算方便，把 三角形对其顶点的平均距离乘以其面积作为一个关于三角形三个顶点的函数。 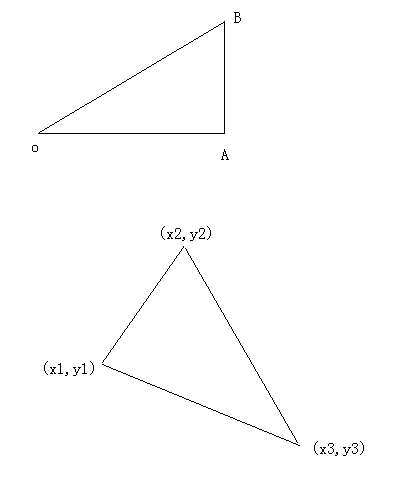d=OA L=AB k=L/d 直角三角形对O点的平均距离乘以面积记作f(d,L). 那么 $f(d,L)=1 / 6 * d ^ 3 * (k * sqrt(k ^ 2 + 1) + ln(k + sqrt(k ^ 2 + 1)))$ ------------------------------------------------- 一般三角形，三个顶点的坐标为(x1,y1),(x2,y2),(x3,y3). 那么三角形对点(x1,y1)的平均距离乘以面积(记作g(x1,y1,x2,y2,x3,y3)) 那么 g(x1,y1,x2,y2,x3,y3) 的计算公式： g(x1,y1,x2,y2,x3,y3)简写成g 设 $t=sqrt((y3 - y2) ^ 2 + (x3 - x2) ^ 2)$ 设$d = ((y3 - y2) * (x1 - x2) + (x2 - x3) * (y1 - y2)) / sqrt((y3 - y2) ^ 2 + (x3 - x2) ^ 2)$ 1.若 t=0或d=0 那么 g=0 2. x = x1 - (y3 - y2) * d/t y = y1 - (x2 - x3) * d/t $d1 = sqrt((x3 - x2) ^ 2 + (y3 - y2) ^ 2)$ $ d2 = sqrt((x - x2) ^ 2 + (y - y2) ^ 2)$ $d3 = sqrt((x - x3) ^ 2 + (y - y3) ^ 2)$ 当d2 < d1 且 d3 < d1 时 $g= f(|d|, d2) + f(|d|, d3)$ 否则 $ g= |f(|d|, d2) -f(|d|, d3)|$ 有了一般三角形的计算平均距离的公式，计算其他复杂图形的公式就非常简单了。根据站点计算图形的分界。再把每个分图形分成以各自站点为顶点的三角形。计算所有三角形的g值的和，除以总面积S就得到总图形的平均距离。对于单位正方形城市，S=1. 总图形的平均距离D=(∑ g)/S= ∑ g

056254628

有了上面的计算公式，只要确定一种站点的设置方案，就可马上利用电脑算出这种方案的平均距离。 假设把正方形城市看成100*100的点阵。那么三个站点的设置有10000^3 种。再利用对称性可以大大减少枚举次数，但觉得计算次数仍太大。 ------------------------------------------------------------ 还有一种方法，就是也随机设定3个站点的位置，利用上述计算公式，用电脑搜索出取最小值时的3个站点位置坐标（最小值的粗糙位置）。当最小值相等，但位置相差较大时，都记录下来。 然后对这些粗糙位置，再对其周围很近的点（上下左右相邻点）进行搜索，找到更精确的最小值位置。

056254628

用上述第二种方法找出的最小值=0.235616744773468 三个站点的坐标如下： 0.234341980267181，0.309584911869812 0.76565804565567 ，0.309584958516846 0.499999957277069，0.791443608965149 ----------------------------------------------------------------- 同34楼算的点位置不同。

mathe

对于区域D内部任意一点(x,y),我们定义 $T(x;y)=int_D sqrt((u-x)^2+(v-y)^2)dudv$ 那么计算Fans心，我们需要找到使得T(x;y)最小的点(x,y) 为此我们需要分别计算T(x;y)的一阶和二阶偏导数，如下: $T_x={del T}/{del x}=int_D {x-u}/{sqrt((u-x)^2+(v-y)^2)}dudv$ $T_y={del T}/{del y}=int_D {y-v}/{sqrt((u-x)^2+(v-y)^2)}dudv$ $T_{x x}={del^2 T}/{del x^2}=int_D{(y-v)^2}/{((u-x)^2+(v-y)^2)^{3/2}}dudv$ $T_{x y}={del^2 T}/{del x del y}=int_D {-(x-u)(y-v)}/{((u-x)^2+(v-y)^2)^{3/2}}dudv$ $T_{y y}={del^2 T}/{del y^2}=int_D{(x-u)^2}/{((u-x)^2+(v-y)^2)^{3/2}}dudv$ 容易看出总是$T_{x x}T_{y y}>=T_{x y}^2$ 也就是函数$T(x;y)$是凸函数，最小值如果存在，那么必然唯一存在，而且我们可以采用牛顿迭代法来找出这个最小值点。 迭代方法如下：搜先我们任意选择一个初始点$(x_0,y_0)$,比如可以选择边界重心作为初始值。 然后对于点$(x_k,y_k)$,如果${(T_x(x*;y*)=0),(T_y(x*;y*)=0):}$而且$(x_k,y_k)$非常接近$(x*,y*)$，那么必然近似的有 $[(0),(0)]~=[(T_x(x_k;y_k)),(T_y(x_k;y_k))]+[(T_{x x}(x_k;y_k),T_{x y}(x_k;y_k)),(T_{x y}(x_k;y_k),T_{y y}(x_k;y_k))][(x*-x_k),(y*-y_k)]$ 于是我们可以采用下面迭代法来逼近Fans心$(x*,y*)$ $[(x_{k+1}),(y_{k+1})]=[(x_k),(y_k)]-[(T_{x x}(x_k;y_k),T_{x y}(x_k;y_k)),(T_{x y}(x_k;y_k),T_{y y}(x_k;y_k))]^-1[(T_x(x_k;y_k)),(T_y(x_k;y_k))]$

mathe

于是下面的问题就是给定一个区域D及其内部一点(x,y),如何有效的计算 $T_x,T_y,T_{x x},T_{x y},T_{y y}$以及最后计算$T(x;y)$,从而得出平均距离 对于我们牵涉到的题目，区域总是一个凸多边形，我们可以先只考虑这种情况。 假设区域的边界凸边形的n个顶点坐标依次为$(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$ 再计算以上各个函数时，为了方便起见，我们可以先进行坐标平移，将目标点(x,y)平移到原点， 于是这时凸边形n个顶点坐标变成$(x'_k=x_k-x,y'_k=y_k-y)$,假设平移以后区域为$D'$ $T_x=-int_{D'}u/{sqrt(u^2+v^2)}dudv$ 然后左边变换为极坐标形式，得到 $T_x=-int_0^{2pi}d\theta int_0^{R(\theta)}rcos(\theta)dr$ 即 $T_x=-1/2int_0^{2pi}R^2(\theta)cos(\theta)d\theta$ 其中$R(\theta)$为$\theta$方向边界到原点（平移前的目标点）的距离 由于边界分段为线段，我们可以对每段线段一次计算，然后累加 假设其中第k段线段法线方向角度为$\theta_k$,到原点距离为$h_k$,那么这个线段上点满足方程$R*cos(\theta-\theta_k)=h_k$ 也就是我们只需要计算线段的方向和到原点的距离，就可以得到$\theta_k$和$h_k$,然后，上面积分中这个线段部分可以化为 而假设第k段线段对原点的张角占的范围为$(t_{k-1},t_k)$, $T_x=-1/2\sum_{k=1}^n int_{t_{k-1}}^{t_k}{h_k^2cos(\theta)}/{cos^2(\theta-\theta_k)}d\theta$ 或者 $T_x=-1/2\sum_{k=1}^n int_{t_{k-1}-theta_k}^{t_k-theta_k}{h_k^2cos(\theta+\theta_k)}/{cos^2(\theta)}d\theta$ 即 $T_x=-1/2\sum_{k=1}^n h_k^2({cos(\theta_k)}/2ln((1+sin(\theta))/(1-sin(theta)))-sin(\theta_k)/cos(\theta))|_{\theta=t_{k-1}-theta_k}^{t_k-theta_k}$ 而$T_y$的计算完全类似 $T_y=-1/2\sum_{k=1}^n h_k^2({sin(\theta_k)}/2ln((1+sin(\theta))/(1-sin(theta)))+cos(\theta_k)/cos(\theta))|_{\theta=t_{k-1}-theta_k}^{t_k-theta_k}$