超级几何难题：六个圆柱相交问题

iseemu2009

    空间中有六个完全一样的半径为 1 的圆柱，它们两两之间的轴线以相同的角度斜交。求相交部分实体的表面积和体积各是多少？

wayne

表面积是$24(2-\sqrt{2})$,体积是$8(2-\sqrt{2})$

1. RegionMeasure[ImplicitRegion[x^2+y^2<=1&&x^2+z^2<=1&&z^2+y^2<=1,{x,y,z}],3]

复制代码

1. RegionMeasure[ImplicitRegion[(x^2 + y^2 == 1 || x^2 + z^2 == 1 || z^2 + y^2 == 1) &&x^2 + y^2 <= 1 && x^2 + z^2 <= 1 && z^2 + y^2 <= 1, {x, y, z}], 2]

复制代码

hejoseph

wayne 发表于 2025-4-25 07:43
表面积是$24(2-\sqrt{2})$,体积是$8(2-\sqrt{2})$

不是这个，看这里
https://mathworld.wolfram.com/SteinmetzSolid.html
最后一个就是，上面算的是三个互相垂直的等圆柱相交部分的几何体，即链接里的第二个几何体。

iseemu2009

这个也就是6个相同的圆柱体，其轴线各自穿过正十二面体6组相对面的中心，形成的交集。

iseemu2009

正十二面体参考图

hejoseph

#1的几何体大概是这样的

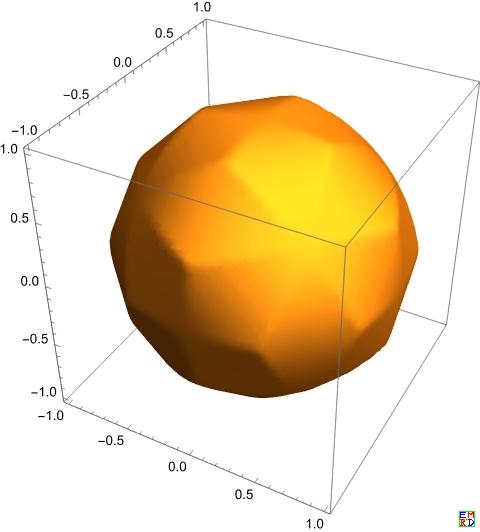
运行以下代码可得到

1. f[X_,Y_,Z_]:=((X^2+Y^2+Z^2) (x^2+y^2+z^2)-(X x+Y y+Z z)^2)/(X^2+Y^2+Z^2)
   
2. C0:=Sqrt[2]/2
   
3. V1:={C0,0,C0}
   
4. V2:={C0,0,-C0}
   
5. V3:={C0,C0,0}
   
6. V4:={C0,-C0,0}
   
7. V5:={0,C0,C0}
   
8. V6:={0,C0,-C0}
   
9. f1:=f[Part[V1,1],Part[V1,2],Part[V1,3]]
   
10. f2:=f[Part[V2,1],Part[V2,2],Part[V2,3]]
    
11. f3:=f[Part[V3,1],Part[V3,2],Part[V3,3]]
    
12. f4:=f[Part[V4,1],Part[V4,2],Part[V4,3]]
    
13. f5:=f[Part[V5,1],Part[V5,2],Part[V5,3]]
    
14. f6:=f[Part[V6,1],Part[V6,2],Part[V6,3]]
    
15. fAll:=f1<=1&&f2<=1&&f3<=1&&f4<=1&&f5<=1&&f6<=1
    
16. RegionPlot3D[fAll,{x,-1,1},{y,-1,1}, {z,-1,1}, PlotPoints->50,Mesh->None]

复制代码

#4的几何体大概是这样的

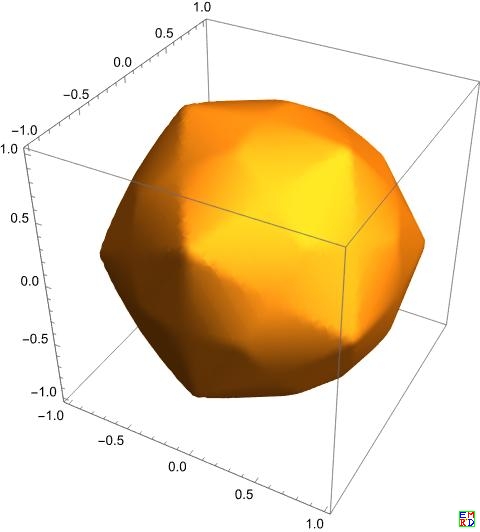
运行以下代码可得到

1. f[X_,Y_,Z_]:=((X^2+Y^2+Z^2) (x^2+y^2+z^2)-(X x+Y y+Z z)^2)/(X^2+Y^2+Z^2)
   
2. C0:=(1+Sqrt[5])/4
   
3. V1:={1/2,0,C0}
   
4. V2:={-1/2,0,C0}
   
5. V3:={C0,1/2,0}
   
6. V4:={-C0,1/2,0}
   
7. V5:={0,C0,1/2}
   
8. V6:={0,-C0,1/2}
   
9. f1:=f[Part[V1,1],Part[V1,2],Part[V1,3]]
   
10. f2:=f[Part[V2,1],Part[V2,2],Part[V2,3]]
    
11. f3:=f[Part[V3,1],Part[V3,2],Part[V3,3]]
    
12. f4:=f[Part[V4,1],Part[V4,2],Part[V4,3]]
    
13. f5:=f[Part[V5,1],Part[V5,2],Part[V5,3]]
    
14. f6:=f[Part[V6,1],Part[V6,2],Part[V6,3]]
    
15. fAll:=f1<=1&&f2<=1&&f3<=1&&f4<=1&&f5<=1&&f6<=1
    
16. RegionPlot3D[fAll,{x,-1,1},{y,-1,1}, {z,-1,1}, PlotPoints->50,Mesh->None]

复制代码

三个互相垂直的圆柱的图

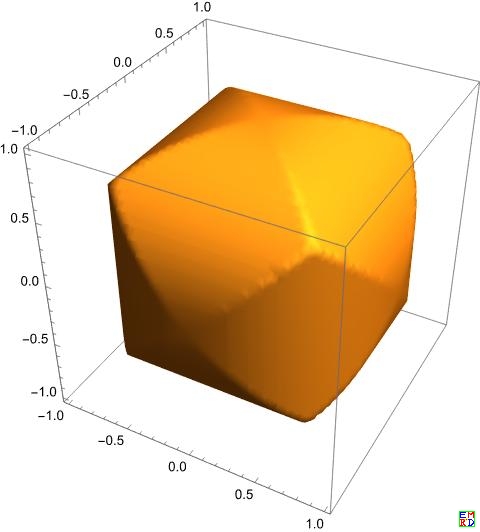
运行以下代码可得到

1. f[X_,Y_,Z_]:=((X^2+Y^2+Z^2) (x^2+y^2+z^2)-(X x+Y y+Z z)^2)/(X^2+Y^2+Z^2)
   
2. V1:={1,0,0}
   
3. V2:={0,1,0}
   
4. V3:={0,0,1}
   
5. f1:=f[Part[V1,1],Part[V1,2],Part[V1,3]]
   
6. f2:=f[Part[V2,1],Part[V2,2],Part[V2,3]]
   
7. f3:=f[Part[V3,1],Part[V3,2],Part[V3,3]]
   
8. fAll:=f1<=1&&f2<=1&&f3<=1
   
9. RegionPlot3D[fAll,{x,-1,1},{y,-1,1}, {z,-1,1}, PlotPoints->50,Mesh->None]

复制代码

hejoseph

可以用链接里的方法去求体积和表面积
第一个几何体是由一个截顶正八面体补上一些圆柱片而成的，如下两个图


第二个几何体是由菱形三十面体补上一些圆柱片而成的，如下个图

再仔细计算一下就可以了，不过计算会很麻烦