- 注册时间
- 2009-3-10
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 2361
- 在线时间
- 小时
|
 发表于 2021-11-1 19:23:20
|
显示全部楼层
发表于 2021-11-1 19:23:20
|
显示全部楼层
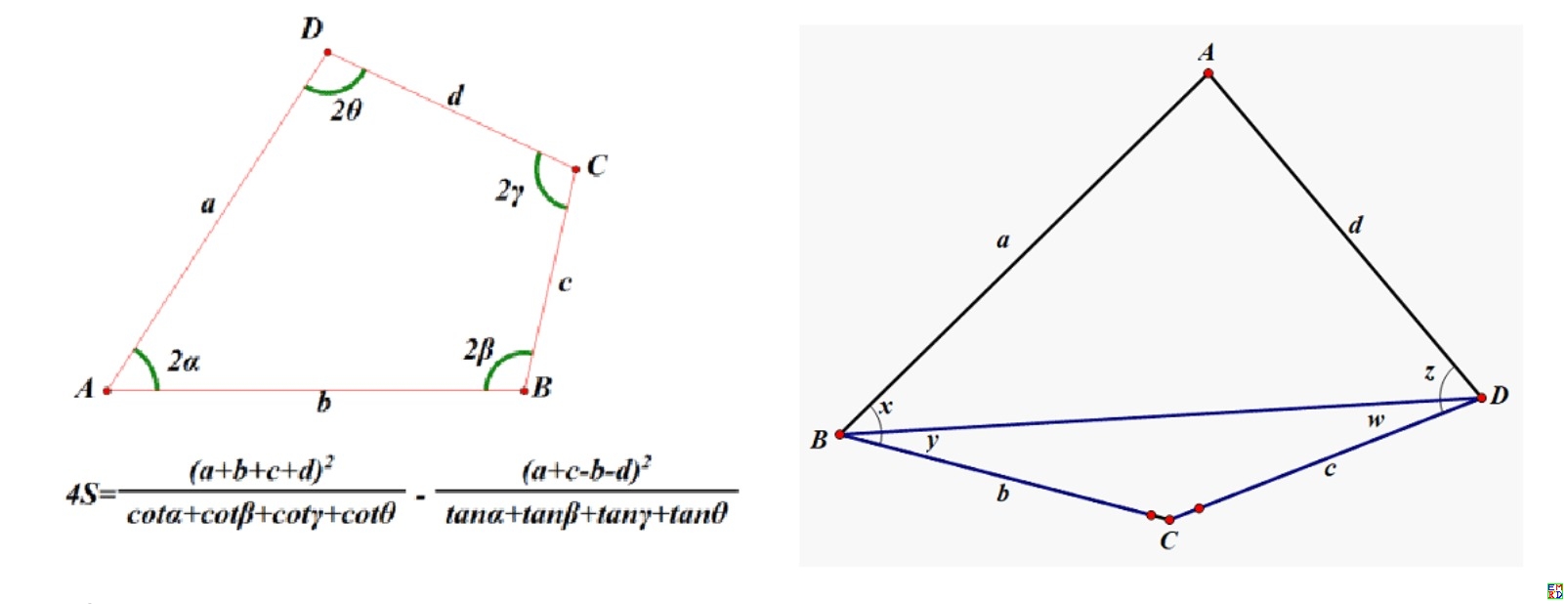
- (*假设BD=1;*)
- a = Sin[z]/Sin[z + x]; d = Sin[x]/Sin[z + x]; b = Sin[w]/
- Sin[y + w]; c = Sin[y]/Sin[y + w];
- A = \[Pi] - (z + x); B = x + y; C1 = \[Pi] - (y + w); D1 = z + w;
- Simplify[{Sin[A], Sin[B], Sin[C1], Sin[D1]}]
- Simplify[{Cot[A], Cot[B], Cot[C1], Cot[D1]}]
- Simplify[{Tan[A], Tan[B], Tan[C1], Tan[D1]}]
- Simplify[{Tan[A/2], Tan[B/2], Tan[C1/2], Tan[D1/2]}]
- S1 = (a + b + c + d)^2/(
- Cot[A/2] + Cot[B/2] + Cot[C1/2] + Cot[D1/2]) - (a - b + c - d)^2/(
- Tan[A/2] + Tan[B/2] + Tan[C1/2] + Tan[D1/2]); S2 =
- 2 (a d Sin[A] + b c Sin[C1]); S3 = 2 (a b Sin[B] + d c Sin[D1]);
- Simplify[{S1, S2, S3, , S1 - S2}]
- (*Factor[{S1,S2,S1-S2}]*)
|
|