三角形内三个四边形的内切圆

hujunhua

按19#的端点说，凹凸临界线也是一个曲边三角形，如下图绿色粗线所示。
这个曲边三角形虽然复杂，但是如果我们找到12#和14#的两个临界点，那么除 了端点，我们还能描出每条曲边上的两点——即与三角形角平分线的交点。
如果Isr314最早提出问题时没有考虑过有一个凹四边形的情况，那么P的区域边界就应该是这个了。

以上图形为2018年12月21日更新，按所说的方法描出了曲线与三角形角平分线的交点共6个，发现长边上有3个，短边上只有1个。
两条较长边是外凸的，而短边近于直线，略有内凹。

mathe

21#的结论比较合理。但是10#和5#中软件画的黑点图是怎么回事？那俩个不是凸四边形情况的图？
由于凹凸变换边界必然对应DPE或EPF或FPD三点共线，而三点共线时，另外两个四边形必然是凸的。也就是只要分别画出DPE三点共线，EPF三点共线和FPD三点共线时的图，就得到了全凸情况的边界了。

10#的三条双曲线边界可以如下解释：
根据9#的分析结论，对于三角形ABC内部给定的P点，边AB上取一点F，那么表达式|AF|-|PF|是关于F点在AB上位置的单调函数，于是其取值范围为 [-|PA|, |AB|-|BP|]。同样在边AC上取一点E,那么表达式|AE|-|PE|是关于E点在AC位置的单调函数，其取值范围为[-|PA|, |AC|-|PC|]。
如果不限定各四边形凹凸性，题目即要求 |AF|-|PF|=|AE|-|PE|,所以这个关系式确定了AB上点F和AC上点E的对应关系，而在$|AB|-|BP|>=|AC|-|PC|$时将线段AB上的一部分一一映射到线段AC的全部；而在$|AB|-|BP|<|AC|-|PC|$时将线段AB的全部一一映射到线段AC的部分（但是A总是映射为A自己）。
同样，另外两条边上的对应关系也构成了类似的映射。这三个映射都会将一条完整的边映射到另外一条边的一部分，而且公共端点会被映射为自己。
注意到$[(|AB|-|BP|)-(|AC|-|CP|)]+[(|BC|-|CP|)-(|BA|-|AP|)]+[(|CA|-|AP|)-(|CB|-|BP|)]=0$,这三个映射中完整的边的选取必然不是全部同向的，也就是必然有两条完整的边被两个映射映射到同一条边上。
不妨设AB被一个关系映射为AC的子线段AX, 而CB被另一个关系映射为CA的子线段CY. 而这时不妨假设BC被第三个关系映射到AB的子线段BZ.
比如下面这个示意图，给出了一种对映关系图

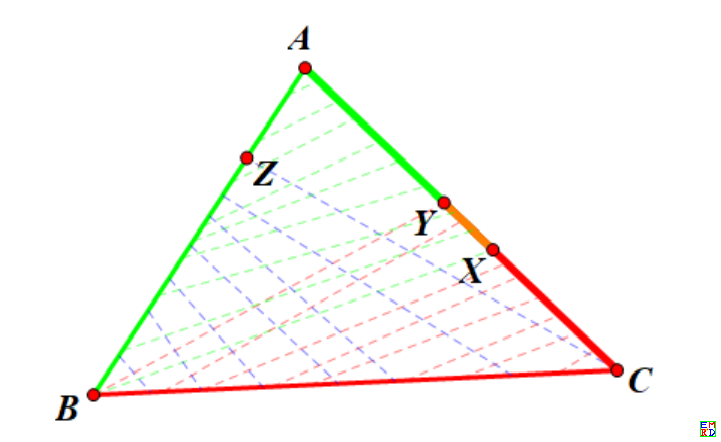
显然如果AX和CY不相交，那么对于给定的P点，我们必然无法找到合法的F和D点满足条件（它们俩分别被绿色和红色映射映射为同一个点E）。
但是如果AX和CY相交，那么经过一轮映射迭代，还是存在合法区间，比如
BC先被红色映射为CY,
其中只有线段XY可以被绿色继续映射为AC的一部分Y'B.
然后Y'B和ZB的公共部分被蓝色映射为BC的一部分
或者逆向上面迭代过程，我们发现一轮迭代后，总是有一个防线会把一个线段映射为其自己的一部分，
所以最后已知迭代下去必然有不动点，也就是可以解出D,E,F.
所以我们可以知道对于给定的P点，存在对应的D,E,F的充分必要条件时AX和CY有公共部分。
对应的边界情况也就是对于给定的P点，X=Y, 也就是|AB|-|BP|=|AX|-|XP|,  |CB|-|BP|=|CX|-|XP|
所以这时必然|AB|-|AX|=|CB|-|CX|=|BP|-|XP|.对应X为三角形ABC内切圆在边AC上的切点，P点轨迹为以B,X为焦点过点A,C的双曲线分支
另外这种情况红绿两种映射都将X和B互为映射，也就是只能选择D=F=B, E=X

lsr314

可以得出一个结论：D、E、F和所在边的中点的有向距离（按逆时针方向）之和为$0$.
当D、E、F都是中点时，如何确定点P的位置？

hujunhua

对于直角三角形，三中点对应的P是直角顶点。

lsr314

当D、E、F都是中点时，点P和三角形ABC的欧拉线非常接近，但是有一点点偏离。

lsr314

不知几何画板能否像标记两条直线的交点一样，准确标记两支双曲线的交点，使得双曲线变化时，交点随之变化？

hujunhua

三中点所对应的 P 点及其划分完全取决于三角形的形状。如果固定三角形的一条边，结果就完全取决于剩下一个点的位置。
设固定的边为BC，位于Y轴上，BC中点在原点，端点坐标为B(0,-3)，C(0,3)。
A为自由顶点。
我们已经知道钝角三角形的P点不存在，直角三角形的P在直角顶点，所以A点就在以BC为宽的带状区域内，但是还要挖去以 BC 为直径的圆内部分。
这个挖洞带状区域的分区可想应为如下：

A在圆上和带状边界上时，△ABC为直角三角形，P在直角顶点。
A离开圆走向圆外时，P离开A，四边形PEAF由无面积退化状态慢慢长出面积，内角\(\angle EPF\approx2\pi-\angle A>\pi\), 故开始为凹四边形。
同理，A刚离开带状边界时，也是进入 凹区。
A继续远离圆周，就会处于一条凹凸分界线上，P在△ABC的一条中位线上，四边形PEAF的边EPF绷直，四边形脱凹成长为三角形。
那条椭圆形的凹凸分界线在x轴上的顶点为`(\pm4,0)`，故猜想它是椭圆\[\frac{x^2}{16}+\frac{y^2}{9}==1\]
用几何画板画图，看起来完全吻合。A在椭圆上时，P在平行于BC的中位线上。
那条蚌形线则是椭圆的反演曲线（基圆为以BC为半径的圆），方程为\[x^2=(|y|+3)^2\frac{3-|y|}{|y|-3/8}\]由反演关系可知，BC是椭圆中以B或者C为端点的最长弦，故P总是在最长中位线上。
从蚌形线的方程可知它有两条渐近线\[y=\pm3/8\]故那两个扳手形凸区，手柄宽度大于并趋近于3/4，并不是一个宽度趋于零的无穷长细尾巴。

mathe

凹凸分界时三角形三边长满足关系式$(b-c)^2(a+b+c)=a^2(5a-3b-3c)$,怎么看也不像是椭圆
由于对于hujunhua的情况有a=6, 我们取方程上一点$(x_0,y_0)=(4\cos(1),3\sin(1))$
计算得出$b=\sqrt(x_0^2+(3-y_0)^2)=2.2129185130824100287954611174957172072, c=\sqrt(x_0^2+(3+y_0)^2)=5.9321129286812417159693577828088709631$
而如果将$a=6,b=2.2129185130824100287954611174957172072$代入三边关系式，解关于c的三次方程，可以得出
$c=5.9526708156868263218532319401591371786$,可以看出hujunhua的椭圆还是很接近真实曲线的，但是的确不匹配

mathe

b-c关系图

两条曲线在第一象限部分的图:

hujunhua

这真是跌破眼镜啊。
说是猜想，只是由于我没有经过计算确认，其实我心里是蛮肯定的，因为画的图看起来“确实”相切，跑一圈都”完全“吻合。
既然有结果了，证明就留给计算强人星空呗，我当时心里就是这么想的。
没想到居然错了！！！这是什么神秘曲线，与椭圆这么的像，难道是双纽线家族的胖子？我还是老老实实补补作业罢。
设`a=2h`, 三角形ABC顶点A的坐标为 `(x, y)`, 则两邻边边长\[b=b(x,y)=\sqrt{x^2+(h-y)^2},c=c(x,y)=b(x,-y)\]代入28#首行的关系式\(5a^3-3a^2(b+c)-(b-c)^2(a+b+c)=0\)中化简可得方程\[x^2=\left(\sqrt{x^2+(h-y)^2}-y-3h\right)\left(\sqrt{x^2+(h+y)^2}+y-3h\right)\]这个确实不像可化成标准椭圆的样子，因为这里是两个根号相乘。但又带着相加减，也不像胖子双纽线。用M10画一下：