三角形内三个四边形的内切圆

数学星空

没想到，小曲边形是12次代数表达式，以下是以ａ＝７，ｂ＝８，ｃ＝９，BC边画出紫色曲线（表达式见PDF）





上图是在下面紫色曲线上取一点验证是否可做内切圆




下面是紫色曲线表达式


表达式.pdf (62.19 KB, 下载次数: 1)

2018-12-20 17:58 上传

点击文件名下载附件

hujunhua

按12#、14#、19#、21#所说的特殊位置，用几何画板描出了凹凸分界线上的9个特殊点（边长7、8、9）。
9个点，大致可以看出凹凸分界线的样子了。

现在发现不计端点，长曲边上有3个特殊点，短曲边上只有1个，1个跑到长边上去了，中间边上恰好保持自己的2个点。
原因在于内心偏向较长的曲边，造成只有一条分角线穿过短边。

lsr314

$D、E、F$都是中点时，假设$A(0,0),B(1,0),C(a,b),P(x,y)$,则
$\sqrt{\frac{1}{4} (a-2 x+1)^2+\left(y-\frac{b}{2}\right)^2}=\frac{1}{2} \left(\sqrt{a^2-2 a+b^2+1}-1\right)+\sqrt{\left(x-\frac{1}{2}\right)^2+y^2},\sqrt{\left(x-\frac{a}{2}\right)^2+\left(y-\frac{b}{2}\right)^2}=\frac{1}{2} \left(\sqrt{a^2+b^2}-1\right)+\sqrt{\left(x-\frac{1}{2}\right)^2+y^2}$
去掉根号：
$2 x^2 \sqrt{a^2-2 a+b^2+1}-a x \sqrt{a^2-2 a+b^2+1}-2 x \sqrt{a^2-2 a+b^2+1}+2 y^2 \sqrt{a^2-2 a+b^2+1}-b y \sqrt{a^2-2 a+b^2+1}+a \sqrt{a^2-2 a+b^2+1}-a^2 x+a^2 \left(-y^2\right)+a^2+2 a b x y-2 a b y+2 a x^2-a x+2 a y^2-a-b^2 x^2+b^2 x+b y-2 x^2+2 x-2 y^2=0$
$2 x^2 \sqrt{a^2+b^2}-a x \sqrt{a^2+b^2}-x \sqrt{a^2+b^2}+2 y^2 \sqrt{a^2+b^2}-b y \sqrt{a^2+b^2}+a^2 x+a^2 \left(-y^2\right)+2 a b x y-2 a x^2+a x-b^2 x^2+b^2 x-2 b x y+b y-y^2=0$
通过结式，可以得到$x,y$各自满足的方程，一般情况表达式太长，不贴出来了，举个例子说明一下，例如$a=1/3,b=2$时，有
$\left(-67323+9056 \sqrt{10}+1703 \sqrt{37}+1664 \sqrt{370}\right) y^4+\left(101940-5932 \sqrt{10}+4268 \sqrt{37}-6028 \sqrt{370}\right) y^3+\left(-48690-754 \sqrt{10}-6034 \sqrt{37}+4790 \sqrt{370}\right) y^2+8 \left(179-71 \sqrt{10}-44 \sqrt{37}+17 \sqrt{370}\right)=4 \left(-6722+1481 \sqrt{10}+380 \sqrt{37}+\sqrt{370}\right) y$
形式非常复杂，实际上，$y$还满足方程$24641 y^4-39104 y^3+12322 y^2-1216 y+36=0$.但是这两个方程并不等价，$y=0.23233312828527633...$是它们唯一的公共根，可以验证，$P$是可以尺规作出的：
$x=\frac{-18 \sqrt{278686660384804-10115608137007 \sqrt{10}+5368772460569 \sqrt{37}-14296986779279 \sqrt{370}}-11468955 \sqrt{10}+8915331 \sqrt{37}-2592133 \sqrt{370}+364058383}{838434666}$
$y=\frac{-\sqrt{2 \left(5953698728765267-1324488517083914 \sqrt{10}-649339874542085 \sqrt{37}+296623702064066 \sqrt{370}\right)}-406053 \sqrt{10}+1117017 \sqrt{37}+2721223 \sqrt{370}+90996659}{279478222}$

mathe

看来的确可以尺规作图，更加一般的，给定任意D,E,F三个点，和三个常数距离$d_1,d_2,d_3$,那么可以尺规作图找到点P,使得
\(\begin{cases}|DP|-|EP|=d_1-d_2\\|EP|-|FP|=d_2-d_3\\ |FP|-|DP|=d_3-d_1\end{cases}\)
当然，这三条条件，本质上还是只有两个条件，满足前两个，那么必然满足第三个。
我们可以取坐标$F(0,0), D(u,1),E(v,1),P(x,y)$
我们先把条件改写为\(|DP|-d_1=|EP|-d_2=|FP|-d_3\),于是得出方程
\(\sqrt{(x-u)^2+(y-1)^2}-d_1=\sqrt{(x-v)^2+(y-1)^2}-d_2=\sqrt{x^2+y^2}-d_3\)
所以
\(\sqrt{(x-u)^2+(y-1)^2}=\sqrt{x^2+y^2}+d_1-d_3\)
两边平方可以得出
\(2(d_1-d_3)\sqrt{x^2+y^2}=-2ux-2y+u^2+1-(d_1-d_3)^2 \tag{1}\)
同理可以得出
\(2(d_2-d_3)\sqrt{x^2+y^2}=-2vx-2y+v^2+1-(d_2-d_3)^2 \tag{2}\)
所以我们得出线性约束
\(\frac{-2ux-2y+u^2+1-(d_1-d_3)^2}{2(d_1-d_3)}=\frac{-2vx-2y+v^2+1-(d_2-d_3)^2}{2(d_2-d_3)} \tag{3}\)
后面只要将(1)式两边平方，并且利用(3)将y用x替换，就可以得出关于x的二次方程。所以x可以表示成二次方程的根，自然可以尺规作图了。

从另外一个角度解释，(1)式代表点P到原点的距离和到一条直线的距离比例是常数，这显然代表以原点为焦点，这条直线为准线的一条圆锥曲线。
所以这里过程代表了有一个公共焦点，而且给定对应准线的两条圆锥曲线的交点可以尺规作图。

上面这个过程也说明了对于本题，不需要要求D、E、F是三边中点，只要给定D、E、F三点，对应的P点位置都可以尺规作图

数学星空

经过长时间的计算有下面结果：

对于{a=7,b=8,c=9}可以得到如下最终的轨迹图





三条红色轨迹曲线方程：

\(-2000\sqrt{5}x^5y-3080\sqrt{5}x^3y^3-1080\sqrt{5}xy^5+82000\sqrt{5}x^4y+31400\sqrt{5}x^2y^3-14364\sqrt{5}y^5+5000x^6+11400x^4y^2+7858x^2y^4+1458y^6-830000\sqrt{5}x^3y-194345\sqrt{5}xy^3-100000x^5-238600x^3y^2-39604xy^4+2982000\sqrt{5}x^2y-432705\sqrt{5}y^3+710000x^4+1874800x^2y^2+479798y^4-3528000\sqrt{5}xy-2100000x^3-5342400xy^2+2205000x^2+7056000y^2=0\)

\(-1000\sqrt{5}x^5y-1540\sqrt{5}x^3y^3-540\sqrt{5}xy^5+41000\sqrt{5}x^4y+15700\sqrt{5}x^2y^3-7182\sqrt{5}y^5+2500x^6+5700x^4y^2+3929x^2y^4+729y^6-443800\sqrt{5}x^3y-78760\sqrt{5}xy^3-50000x^5-119300x^3y^2-19802xy^4+1894200\sqrt{5}x^2y-431760\sqrt{5}y^3+355000x^4+865100x^2y^2+256894y^4-3175200\sqrt{5}xy-1050000x^3-2442300xy^2+1102500x^2+5468400y^2=0\)

\(-2000\sqrt{5}x^5y-3080\sqrt{5}x^3y^3-1080\sqrt{5}xy^5+82000\sqrt{5}x^4y+31400\sqrt{5}x^2y^3-14364\sqrt{5}y^5+5000x^6+11400x^4y^2+7858x^2y^4+1458y^6-786800\sqrt{5}x^3y-173025\sqrt{5}xy^3-100000x^5-238600x^3y^2-39604xy^4+2679600\sqrt{5}x^2y-830025\sqrt{5}y^3+710000x^4+1637800x^2y^2+517638y^4-3528000\sqrt{5}xy-2100000x^3-3481800xy^2+2205000x^2+7056000y^2=0\)

数学星空

对于一般情况是否存在三个等圆的内切圆？答案待定，但有以下结论：

对于一般情况，若要求有两个圆半径相等，记\(PD=x,PE=y,PF=z,P(x0,y0)\)，若EF平行于底边则(另外两种情形即DE或DF平行于对应的侧边未列出)

\(4a(a^3+a^2b+a^2c-5ab^2+10abc-5ac^2+3b^3-3b^2c-3bc^2+3c^3)x0^2+(-4a^5-4a^4b-4a^4c+24a^3b^2-40a^3bc+16a^3c^2-16a^2b^3+40a^2b^2c-16a^2bc^2-8a^2c^3-4ab^4+8ab^3c-8abc^3+4ac^4+4b^5-4b^4c-8b^3c^2+8b^2c^3+4bc^4-4c^5)x0+a(a+b+c)(a^2+2ab-2ac-3b^2+2bc+c^2)(-b+c+a)^2=0\)

\((2a^3+2a^2b+2a^2c-10ab^2+20abc-10ac^2+6b^3-6b^2c-6bc^2+6c^3)x^2-(2(a-b-c))(a^3+a^2b+a^2c-7ab^2+14abc-7ac^2+b^3-b^2c-bc^2+c^3)x+a(a-b-c)(a^3+a^2b+a^2c-5ab^2+10abc-5ac^2+3b^3-3b^2c-3bc^2+3c^3)=0\)

\(c^7+3ba^6+b^7+a^5b^2-5a^4b^3-5a^3b^4+a^2b^5-3a^5c^2+3a^4c^3+3a^3c^4-3a^2c^5-3b^5c^2+3b^4c^3+3b^3c^4-3b^2c^5-a^6c-ac^6-b^6c-bc^6+(4a^5+12a^4b+12a^4c-8a^3b^2+64a^3bc-8a^3c^2-24a^2b^3+40a^2b^2c+40a^2bc^2-24a^2c^3+4ab^4-8ab^2c^2+4ac^4+12b^5+12b^4c-24b^3c^2-24b^2c^3+12bc^4+12c^5)y^2+(8a^4b^2-16a^4bc+8a^4c^2+16a^3b^3-32a^3b^2c+16a^3bc^2-16a^2b^3c+16a^2b^2c^2+16a^2bc^3-16a^2c^4-16ab^5+32ab^3c^2-16abc^4-8b^6+24b^4c^2-24b^2c^4+8c^6)y+a^7+3ab^6-2a^5bc-7a^4bc^2+4a^3b^3c+2a^2b^2c^3-2ab^5c+4a^3bc^3+5ab^2c^4-2abc^5+4ab^3c^3-7ab^4c^2+a^4b^2c-6a^2b^3c^2+5a^2bc^4-6a^3b^2c^2+a^2b^4c=0\)

\(c^7-ba^6+b^7-3a^5b^2+3a^4b^3+3a^3b^4-3a^2b^5+a^5c^2-5a^4c^3-5a^3c^4+a^2c^5-3b^5c^2+3b^4c^3+3b^3c^4-3b^2c^5+3a^6c+3ac^6-b^6c-bc^6+(4a^5+12a^4b+12a^4c-8a^3b^2+64a^3bc-8a^3c^2-24a^2b^3+40a^2b^2c+40a^2bc^2-24a^2c^3+4ab^4-8ab^2c^2+4ac^4+12b^5+12b^4c-24b^3c^2-24b^2c^3+12bc^4+12c^5)z^2+(8a^4b^2-16a^4bc+8a^4c^2+16a^3b^2c-32a^3bc^2+16a^3c^3-16a^2b^4+16a^2b^3c+16a^2b^2c^2-16a^2bc^3-16ab^4c+32ab^2c^3-16ac^5+8b^6-24b^4c^2+24b^2c^4-8c^6)z+a^7-ab^6-2a^5bc+a^4bc^2+4a^3b^3c-6a^2b^2c^3-2ab^5c+4a^3bc^3-7ab^2c^4-2abc^5+4ab^3c^3+5ab^4c^2-7a^4b^2c+2a^2b^3c^2+a^2bc^4-6a^3b^2c^2+5a^2b^4c=0\)

\(20bc^9a^2-8b^5c^5a^2+c^{12}-40bc^7a^4+4bca^{10}+20b^9ca^2-6b^{10}a^2-44b^4a^6c^2-20a^8b^3c+26a^8b^2c^2-20a^8bc^3+(4a^9b+4a^9c+4a^8b^2+8a^8bc+4a^8c^2-32a^7b^3+16a^7b^2c+16a^7bc^2-32a^7c^3+16a^6b^4-80a^6b^3c+64a^6b^2c^2-80a^6bc^3+16a^6c^4+40a^5b^5-8a^5b^4c-32a^5b^3c^2-32a^5b^2c^3-8a^5bc^4+40a^5c^5-40a^4b^6+128a^4b^5c-216a^4b^4c^2+256a^4b^3c^3-216a^4b^2c^4+128a^4bc^5-40a^4c^6-48a^3b^6c+144a^3b^5c^2-96a^3b^4c^3-96a^3b^3c^4+144a^3b^2c^5-48a^3bc^6+16a^2b^8-48a^2b^7c+32a^2b^6c^2+48a^2b^5c^3-96a^2b^4c^4+48a^2b^3c^5+32a^2b^2c^6-48a^2bc^7+16a^2c^8-12ab^9+36ab^8c-96ab^6c^3+72ab^5c^4+72ab^4c^5-96ab^3c^6+36abc^8-12ac^9+4b^10-8b^9c-12b^8c^2+32b^7c^3+8b^6c^4-48b^5c^5+8b^4c^6+32b^3c^7-12b^2c^8-8bc^9+4c^10)y0^2-24b^3c^5a^4+15c^8a^4+28b^6c^6-8b^5c^7-17b^4c^8+12b^3c^9-16b^7c^3a^2+26b^4c^4a^4+48b^3a^6c^3+40b^5a^6c+20b^6c^4a^2+36b^6c^2a^4+2b^2c^{10}-4bc^{11}-24b^5c^3a^4+40ba^6c^5-20b^6a^6-20c^6a^6-4b^{11}c+2b^{10}c^2+12b^9c^3-17b^8c^4-8b^7c^5+15a^8b^4+15a^8c^4+15b^8a^4-6c^{10}a^2+b^{12}+36b^2c^6a^4-14b^2c^8a^2-16b^3c^7a^2-6b^2a^{10}-40b^7ca^4+(4a^8+8a^7b+8a^7c-36a^6b^2+88a^6bc-36a^6c^2-16a^5b^3+16a^5b^2c+16a^5bc^2-16a^5c^3+124a^4b^4-400a^4b^3c+552a^4b^2c^2-400a^4bc^3+124a^4c^4-120a^3b^5+360a^3b^4c-240a^3b^3c^2-240a^3b^2c^3+360a^3bc^4-120a^3c^5+36a^2b^6-72a^2b^5c-36a^2b^4c^2+144a^2b^3c^3-36a^2b^2c^4-72a^2bc^5+36a^2c^6)y0^4+a^{12}-44b^2a^6c^4-6c^2a^{10}+20b^4c^6a^2-14b^8c^2a^2=0\)

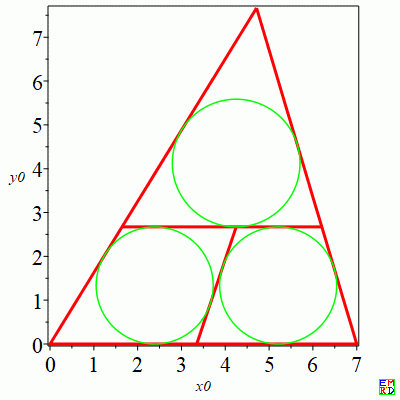
例取\({a=7,b=8,c=9}\)

得到

\({a = 7, b = 8, c = 9, s = 12\sqrt{5}, x = 2.818895425, x0 = 4.248875272, y = 1.954723856, y0 = 2.671209728, z = 2.606298475}\)

画图得到

数学星空

对于存在三个等内切圆时,且EF平行于底边BC时三角形三边需满足关系

\(5a^4-2a^2b^2-2a^2c^2-3b^4+6b^2c^2-3c^4=0\)

此时内切圆半径\(r\)满足下列方程:

\((6400b^4-24800b^3c+36825b^2c^2-24800bc^3+6400c^4)r^8+(-880b^6+4360b^5c-10120b^4c^2+13245b^3c^3-10120b^2c^4+4360bc^5-880c^6)r^6+(64b^8-288b^7c+775b^6c^2-1584b^5c^3+2067b^4c^4-1584b^3c^5+775b^2c^6-288bc^7+64c^8)r^4+(-20b^8c^2+76b^7c^3-122b^6c^4+132b^5c^5-122b^4c^6+76b^3c^7-20b^2c^8)r^2+b^8c^4-4b^7c^5+6b^6c^6-4b^5c^7+b^4c^8=0\)

例如取\(b=8,c=9\)

并利用楼上的公式可以得到

\({a = 7.8006183588  ,x = 3.012220437, x0 = 4.628006141, y = 2.087274709, y0 = 2.892278183, z = 2.701123215}\)

画图得到

lsr314

数学星空 发表于 2018-12-26 21:10
对于存在三个等内切圆时,三角形三边需满足关系:

\(5a^4-2a^2b^2-2a^2c^2-3b^4+6b^2c^2-3c^4=0\)

为啥存在的条件关于abc不对称呢？

lsr314

数学星空 发表于 2018-12-26 21:10
对于存在三个等内切圆时,三角形三边需满足关系:

\(5a^4-2a^2b^2-2a^2c^2-3b^4+6b^2c^2-3c^4=0\)

a=b=c=1不满足这个等式，但此时显然是存在的。原因估计是默认上面这个圆与下面两个圆的公切线相切了，但是正三角形不是这样的，其他三角形也可能存在这种情况。

lsr314

数学星空 发表于 2018-12-26 21:10
对于存在三个等内切圆时,三角形三边需满足关系EF平行于底边BC时)

\(5a^4-2a^2b^2-2a^2c^2-3b^4+6b^2c^ ...

一般的情况可以这样作图：先从一点P向外做三条射线，然后在三个角的角平分线上各取一点，以这一点为圆心作与角的两边相切的圆，通过移动点的位置，可以让三个圆的半径相等，然后作这三个圆的两两外公切线，得到三个交点，以这三个交点为顶点的三角形，就存在三个等圆，而此时三角形的形状完全由开始的三条射线的夹角确定，并不一定是正三角形。