三角形内三个四边形的内切圆

hujunhua

胖子双纽线\[x^2+\frac{14}9 y^2+1=\sqrt{4x^2+15^2}\]与椭圆的对比图

仔细比较两图，发现胖子双纽线（四次曲线）更接近于椭圆，两者几乎无缝矣，蓝色的胖子线基本上看不到了。

hujunhua

虽然比较肯定这个椭圆，但是有两点曾引起我怀疑，然终未驱走我的懒病，去做个计算验证。

第一点：由于短轴BC是三角形ABC的最长边，所以是椭圆中从短轴一个端点出发的最长弦。我认为这个椭圆应该是满足这一性质的最扁椭圆。因此椭圆在B处的曲率圆圆心应在短轴的另一端C点处。
但用几何画板画图验证表明，B处的曲率圆圆心在C点下方一点点，即曲率半径比BC小一点点。这个不完美曾让我感到遗憾，但也只是表示了一下无奈，未能促使去计算其方程。

第二点：27#那个扳手柄居然有非零宽度，而不是一条无穷长细尾巴，这违反我事先的定性推理。面对这个矛盾，我选择了让步，认为我事先的定性推理错了。

wayne

哈哈，胖子双纽线 太混淆直觉了。特地搜了下，是这个吧
http://mathworld.wolfram.com/CassiniOvals.html，Giovanni Domenico Cassini的卵形线， ^_^

hujunhua

@数学星空

如图，由圆外切四边形的性质定理有\[BD+FP=BF+DP\\CD+EP=CE+DP\]上下两式相加可得\[2DP=3/2a-(b+c)/2\]所作`AG\varparallel DP`,易见BC边的中点`D`也是`GH`的中点, 所以\[\begin{split}BG&=CH=(a+b-c)/2\\AG&=2DP=3/2a-(b+c)/2\end{split}\]在三角形ABC和三角形ABG中应用余弦定理可得\[\cos B=\frac{AB^2+BG^2-AG^2}{2AB\cdot BG}=\frac{a^2+c^2-b^2}{2ac}\]将`AG=3/2a-(b+c)/2,AB=c,BG=(a+b-c)/2`代入上式整理可得\[(b-c)^2(a+b+c)=a^2(5a-3b-3c)\]
为了在几何画板中画出图中的曲线，我是设`a=1,x=b-c，y=b+c`代入化为\[y=\frac8{x^2+3}-1\]画出函数曲线然后在曲线上取点，将点坐标转化为`b,c`即可作轨迹得到图中曲线。

hujunhua

30#所得到的方程\[x^2=\left(\sqrt{x^2+(h-y)^2}-y-3h\right)\left(\sqrt{x^2+(h+y)^2}+y-3h\right)\]是一条十分接近某个椭圆的凸曲线，确实是一个很令人惊异的结果。为使系数较小，令`h=1`, 曲线方程去根号有理化的结果为\[\left(4y^2-\frac{(4-3x) (2+x)^2}{4+x}\right)\left(4y^2-\frac{(4+3x) (2-x)^2}{4-x}\right)=0\]原来曲线是一条六次曲线的一部分。这条六次曲线由两条三次曲线（迪卡尔叶形线的仿射类）合成。`h=3`时如下图中的天蓝色曲线和橘黄色曲线：

lsr314

还有两个问题：
一是，什么情况下存在一个划分，使得三个圆的半径相同，并求其半径。
二是，当D、E、F都是中点时，点P和三角形ABC的欧拉线非常接近，能否给出解释。

数学星空

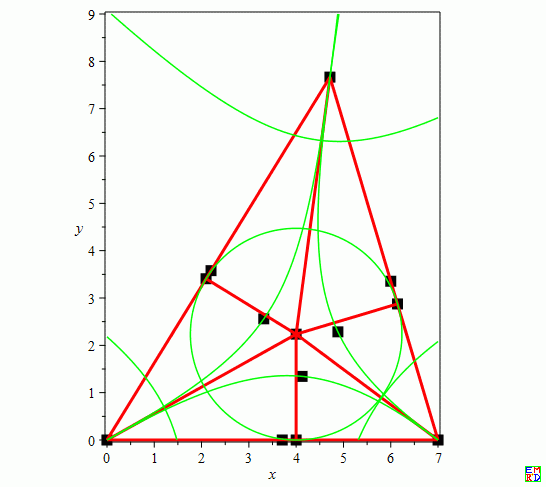
我们可以建立坐标系求解轨迹曲线(大曲边双曲线方程)

以B点为坐标原点,分别设\(A(x1,y1),B(0,0),C(a,0),P(x0,y0),PD=x,PE=y,PF=z,s\)为三角形ABC面积,\(t=\tan(\frac{\theta}{2})\)则有以下结论:

设分别以AB,BC,CA为弦的双曲线方程

\(\frac{((x-x0)\cos(\theta)-(y-y0)\sin(\theta))^2}{a1^2}-\frac{((x-x0)\sin(\theta)+(y-y0)\cos(\theta))^2}{b1^2}=1\)

1.以BC为弦的双曲线参数满足:

\(a1=\frac{(b+c-a)}{4}\)

\(b1=s\sqrt{\frac{2}{a(a+b+c)}}\)

\(x0=\frac{2a^2-ab+ac-b^2+c^2}{4a}\)

\(y0=\frac{s}{a}\)

\((a+b-c)(c+a+b)(a-b+c)t^4+(-2a^3-2a^2b-2a^2c+6ab^2-12abc+6ac^2-2b^3+2b^2c+2bc^2-2c^3)t^2+(a+b-c)(c+a+b)(a-b+c)=0\)

2.以AC为弦的双曲线参数满足:

\(a1=\frac{(a+c-b)}{4}\)

\(b1=s\sqrt{\frac{2}{b(a+b+c)}}\)

\(x0=-\frac{a^3-3a^2b-a^2c+ab^2-ac^2+b^3-b^2c-bc^2+c^3}{8ab}\)

\(y0=\frac{s(a+b-c)}{2ab}\)

\((c+a+b)(-b-c+a)(a+b-c)^3t^4+(2a^5-26a^4b-6a^4c+20a^3b^2+48a^3bc+4a^3c^2+12a^2b^3+4a^2b^2c-20a^2bc^2+4a^2c^3-6ab^4+12ab^2c^2-6ac^4-2b^5+2b^4c+4b^3c^2-4b^2c^3-2bc^4+2c^5)t^2+(c+a+b)(-b-c+a)(a+b-c)^3=0\)

3.以AB为弦的双曲线参数满足:

\(a1=\frac{(a+b-c)}{4}\)

\(b1=s\sqrt{\frac{2}{c(a+b+c)}}\)

\(x0=\frac{a}{2}+\frac{a^3-a^2b+a^2c-ab^2+ac^2+b^3-b^2c-bc^2+c^3}{8ac}\)

\(y0=\frac{s(a-b+c)}{2ac}\)

\((c+a+b)(-b-c+a)(c+a-b)^3t^4+(2a^5-6a^4b-26a^4c+4a^3b^2+48a^3bc+20a^3c^2+4a^2b^3-20a^2b^2c+4a^2bc^2+12a^2c^3-6ab^4+12ab^2c^2-6ac^4+2b^5-2b^4c-4b^3c^2+4b^2c^3+2bc^4-2c^5)t^2+(c+a+b)(-b-c+a)(c+a-b)^3=0\)

例:将\({a=7,b=8,c=9,s=12\sqrt{5}}\)代入可以得到大曲边双曲线方程

\(-29.75209291x^2+(13.30567350y+208.2646503)x+41.03452321y^2-372.5588586y=0\)

\(5.984780734x^2+(9.725970419y-50.74342095)x-2.129903001y^2-23.74882954y+61.94969066=0\)

\(471.3607528x^2+(-1046.399584y-2504.534952)x+81.7005314y^2+4480.324490y=0\)

画图得到:

lsr314

能否证明：D、E、F都是中点时，点P是可以尺规作出的

mathe

两条双曲线的交点，对应四次方程的解，通常是不能尺规作图的

lsr314

mathe 发表于 2018-12-20 10:40
两条双曲线的交点，对应四次方程的解，通常是不能尺规作图的

通过几个例子计算表明，D、E、F都是中点时，点P都是可以尺规作图的，所以提出这个问题，不知是否能证出来。