有理表示在初等欧氏几何中的应用

TSC999

楼主的文章非常好，不知楼主能否继续发布剩余论文。

TSC999

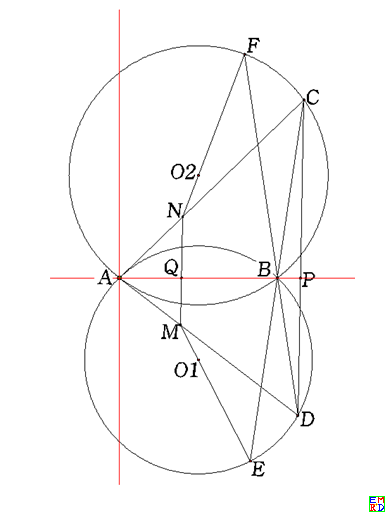
楼主先生，您前几天在回复另一帖子中发布了如下程序，在学习该程序时，觉得最后显示的那个结论公式太复杂，它应该等于零才对。

我试着改了一下最后那条语句，计算表明两组线段长度之比确实等于零。我觉得我改写后的语句可能还不是最优的，有没有更好的写法？

1. Clear["Global`*"];   (*creasson编写的有理参数构图程序*)
   
2. points = {A -> 0, B -> 1, P -> (1 + I p)/(1 - I u),
   
3.   T -> (1 + I q)/(1 - I v)};(*设点*)
   
4. vectors =
   
5. Factor[{v1 -> Limit[D[P /. points, u]*u^2, u -> \[Infinity]],
   
6.    v2 -> Limit[D[T /. points, v]*v^2,
   
7.      v -> \[Infinity]]}];(*在A处的两条切线的切向量*)
   
8. CDEQ = (Factor[ComplexExpand[Im[#]]] //
   
9.      Numerator) & /@ ({(T - A)/v1, (P - A)/v2} /. points /.
   
10.     vectors);(*求C,D*)
    
11. CDsol = Solve[CDEQ == 0, {u, v}] // Flatten;
    
12. points = Union[
    
13.     points, {C -> (T /. points /. CDsol),
    
14.      D -> (P /. points /. CDsol)}] // Factor;
    
15. (*求E,F*)
    
16. EFEQ = (Factor[ComplexExpand[Im[#]]] //
    
17.       Numerator) & /@ ({(P - B)/(C - B), (T - B)/(D - B)} /. points);
    
18. EFsol = Solve[EFEQ == 0, {u, v}][[-1]];
    
19. points = Union[
    
20.     points, {E -> (P /. points /. EFsol),
    
21.      F -> (T /. points /. EFsol)}] // Factor;
    
22. (*求M,N*)
    
23. points = Union[points, {O1 -> (1 + I p)/2, O2 -> (1 + I q)/2}] //
    
24.    Factor;
    
25. points = Union[
    
26.     points, {M -> \[Lambda]*D + (1 - \[Lambda]) A,
    
27.       N -> \[Mu]*C + (1 - \[Mu]) A} /. points] // Factor;
    
28. MNEQ = (Factor[ComplexExpand[Im[#]]] //
    
29.       Numerator) & /@ ({(M - O1)/(E - O1), (N - O2)/(F - O2)} /.
    
30.      points);
    
31. MNsol = Solve[MNEQ == 0, {\[Lambda], \[Mu]}] // Flatten;
    
32. points = Factor[points /. MNsol];(*求点Q*)
    
33. points = Union[points, {Q -> \[Eta]}] // Factor;
    
34. QEQ = (Factor[ComplexExpand[Im[#]]] //
    
35.       Numerator) & /@ ({(M - Q)/(N - Q)} /. points);
    
36. Qsol = Solve[QEQ == 0, {\[Eta]}] // Factor // Flatten;
    
37. points = Factor[points /. Qsol];
    
38. 
    
39. squarelens =
    
40. Factor[ComplexExpand[Abs[#]^2]] & /@ ({B - D, B - C, Q - M,
    
41.      Q - N} /. points);(*结论*)
    
42. target = Factor[(squarelens[[1]]/squarelens[[2]]) - (squarelens[[3]]/
    
43.      squarelens[[4]])];
    
44. Print["points = ", points];(*显示*)
    
45. (*Print["target = ",target]; 原语句 *)
    
46. Print["target = ",
    
47. Simplify[target]];(*把上面的原语句加上Simplify，计算结果会简化一些，但还不是最简*)
    
48. (*把上面的原语句改为下面几条语句，将给出目标式的最简结果*)
    
49. k1 = ExpandDenominator@
    
50.   Together@ComplexExpand@Simplify[Abs[(B - D)/(B - C)] /. points];
    
51. k2 = ExpandDenominator@
    
52.    Together@ComplexExpand@Simplify[Abs[(Q - M)/(Q - N)] /. points];
    
53. DB/BC -> k1
    
54. MQ/NQ -> k2
    
55. If[k1 - k2 == 0, Print["由于 DB/BC-MQ/NQ = 0，所以 DB/BC = MQ/NQ"]]

复制代码

程序运行结果如下（用图片表示：）

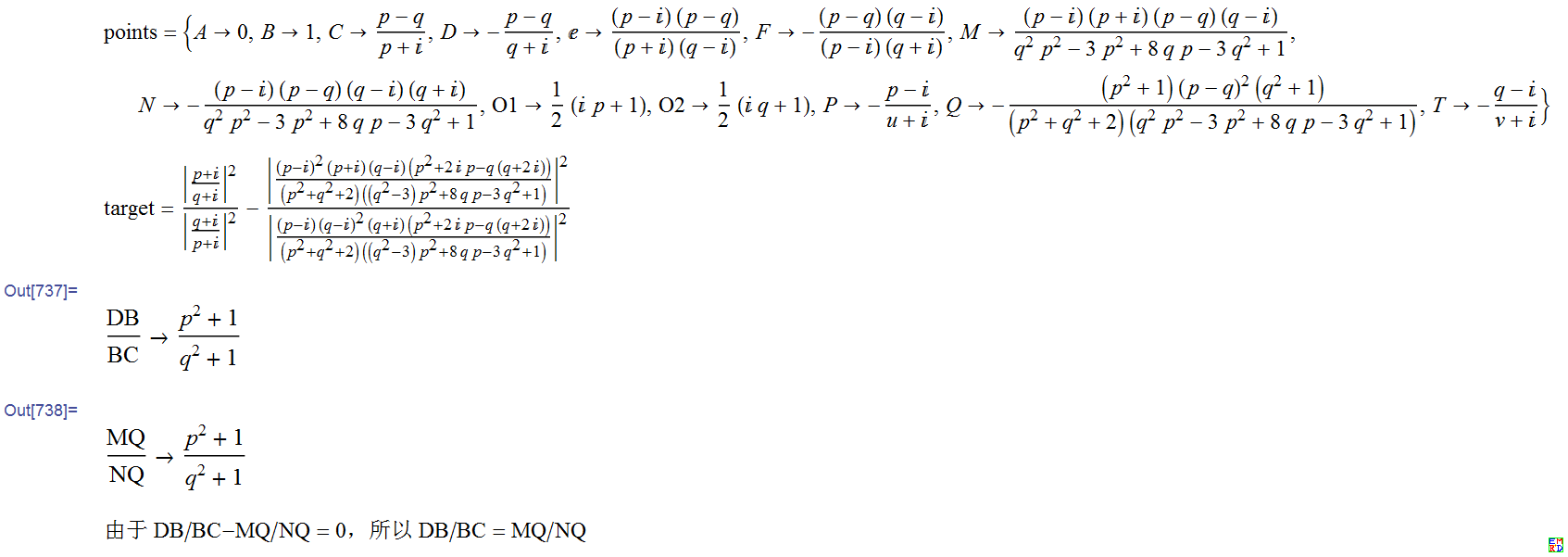
creasson

TSC999 发表于 2021-10-8 20:11
楼主先生，您前几天在回复另一帖子中发布了如下程序，在学习该程序时，觉得最后显示的那个结论公式太复杂， ...

您客气， 改为如下就好了:

1. values = Factor[
   
2.      ComplexExpand[
   
3.       Abs[#]]] & /@ (Factor[{(B - D)/(B - C), (Q - M)/(Q - N)} /.
   
4.       points]);
   
5. DB/BC -> values[[1]]
   
6. MQ/NQ -> values[[2]]
   
7. If[values[[1]] - values[[2]] == 0,
   
8. Print["由于 DB/BC-MQ/NQ = 0，所以 DB/BC = MQ/NQ"]]

复制代码

dlsh

楼主与我的最大共识是向量商，不过学术界争议很大。

creasson

dlsh 发表于 2021-10-9 20:32
楼主与我的最大共识是向量商，不过学术界争议很大。

向量商不是必要的概念，可以只用共轭乘积， 只因向量商的表示更简单一些。复斜率就完全没必要了, 切向量是最合适的。学术界有争议倒没关系，只要能自圆其说，都是好工具。

dlsh

不用向量商如何描述这条结论，用直线方程求解、判断角相等复斜率当然有必要。

向量商之和

无论三角形内外，都有：
\(\frac{\overrightarrow{OD}}{\overrightarrow{AD}}+\frac{\overrightarrow{OE}}{\overrightarrow{BE}}+\frac{\overrightarrow{OF}}{\overrightarrow{CF}}=1\)

dlsh

http://www.mathchina.com/bbs/for ... =2046876&extra=

creasson

dlsh 发表于 2021-10-10 23:08
不用向量商如何描述这条结论，用直线方程求解、判断角相等复斜率当然有必要。

无论三角形内外，都有： ...

用不使用向量商概念的体系来证明一个向量商表示的等式，这是难以做到的。不过也不是完全没办法
可以改造等式为
\[\frac{{\mathop {BC}\limits^ \to   \otimes \mathop {AH}\limits^ \to  }}{{\mathop {AH}\limits^ \to   \otimes \mathop {AH}\limits^ \to  }}{\rm{ + }}\frac{{\mathop {CA}\limits^ \to   \otimes \mathop {BH}\limits^ \to  }}{{\mathop {BH}\limits^ \to   \otimes \mathop {BH}\limits^ \to  }} + \frac{{\mathop {AB}\limits^ \to   \otimes \mathop {CH}\limits^ \to  }}{{\mathop {CH}\limits^ \to   \otimes \mathop {CH}\limits^ \to  }} =  - \frac{{\mathop {BC}\limits^ \to   \otimes \mathop {AH}\limits^ \to  }}{{\mathop {AH}\limits^ \to   \otimes \mathop {AH}\limits^ \to  }} \cdot \frac{{\mathop {CA}\limits^ \to   \otimes \mathop {BH}\limits^ \to  }}{{\mathop {BH}\limits^ \to   \otimes \mathop {BH}\limits^ \to  }} \cdot \frac{{\mathop {AB}\limits^ \to   \otimes \mathop {CH}\limits^ \to  }}{{\mathop {CH}\limits^ \to   \otimes \mathop {CH}\limits^ \to  }}\]

这个表示复杂一些，不过可以用共轭乘积来做。
\[\mathop b\limits^ \to   \otimes \mathop a\limits^ \to   = |\mathop a\limits^ \to  |{\rm{|}}\mathop b\limits^ \to  |\cos \theta  + i|\mathop a\limits^ \to  |{\rm{|}}\mathop b\limits^ \to  |\sin \theta \]
其中$ \theta $为由向量$ \vec {a} $ 逆时针旋转为$ \vec {b} $ 所经历的角度。右方实部为通常的内积，虚部为通常的外积。 在一般$n$维空间上则是由cllifford所定义的运算。

三点共线也就是三角形的面积为0：
\[{\mathop{\rm Im}\nolimits} (\mathop {AB}\limits^ \to   \otimes \mathop {AC}\limits^ \to  ) = 0\]
或者
\[{\mathop{\rm Im}\nolimits} (\mathop {OA}\limits^ \to   \otimes \mathop {OB}\limits^ \to   + \mathop {OB}\limits^ \to   \otimes \mathop {OC}\limits^ \to   + \mathop {OC}\limits^ \to   \otimes \mathop {OA}\limits^ \to  ) = 0\]

至于角度，则是
\[{e^{i\theta }} = \frac{{\mathop b\limits^ \to   \otimes \mathop a\limits^ \to  }}{{|\mathop b\limits^ \to  ||\mathop a\limits^ \to  |}}\]

以上也就避开了直接使用向量商，当然，由向量共轭乘积的定义也可以导出向量商。这些在书中都有写到。

creasson

我并不把 $ \frac{\vec {b}} {\vec {a}} $ 看作是$ \vec {b} $ 除以 $ \vec {a} $ ，而仅是当做由 $ \vec {a} $ 到$ \vec {b} $ 所经历的一个旋转缩放变换，它可以用其它的记号来表示，只是 $ \frac{\vec {b}} {\vec {a}} $的表示更简明，而且当 $ \vec {a} $, $ \vec {b} $取复数形式时，它与通常的除法定义无区别。

creasson

不过也感谢你@dlsh提出了这一问题，使得我意识到应将书中除法定义放在共轭乘积定义之后，否则有点本末倒置的意味。