有理表示在初等欧氏几何中的应用

王守恩

dlsh 发表于 2021-10-10 23:08
不用向量商如何描述这条结论，用直线方程求解、判断角相等复斜率当然有必要。

无论三角形内外，都有： ...

梅氏定理，根据16楼大一点的图，可以用6次。

\(1,A+△ODB:\frac{AO*EB*CD}{AD*EO*CB}=1\)

\(2,B+△CDA:\frac{BC*EA*OD}{BD*EC*OA}=1\)

\(3,B+△AFC:\frac{BA*EC*OF}{BF*EA*OC}=1\)

\(4,C+△OFB:\frac{CO*EB*AF}{CF*EO*AB}=1\)

\(5,D+△CBF:\frac{DC*OF*AB}{DB*OC*AF}=1\)

\(6,F+△ABD:\frac{FA*OD*CB}{FB*OA*CD}=1\)

    \(2*6=\frac{BD*CE*AF}{CD*EA*FB}=1\)

别想复杂，注意这里字母的排列，梅氏定理也只能用6次。

dlsh

一般情形

上图重画你书中21页证明相似的例子 ，字母标记不同，题中的比例为2是特例.容易用同一法验证。

大漠孤烟

个人感觉作者的方法很强大，还得花时间去学习，但是有些结论表示过于复杂了。究其原因，就像数列的通项公式和递推公式的区别，这种结论表示方法求出了数量的绝对关系，没有展现出同类几何量之间的相对关系，所以显得复杂。如果能用作者的方法进一步总结，求出几何对象的线段之间、角度之间、半径之间、位置之间的相对关系（就像几何定理一样），结论说不定简化很多，用看起来复杂的过程得出异常简洁的结果，肯定会吸引人去阅读作者的书。

dlsh

王守恩 发表于 2021-10-11 13:02
梅氏定理，根据16楼大一点的图，可以用6次。

\(1,A+△ODB:\frac{AO*EB*CD}{AD*EO*CB}=1\)

Ceva定理向量商表示：\(\frac{\overrightarrow{BD}}{\overrightarrow{CD}}\frac{\overrightarrow{CE}}{\overrightarrow{EA}}\frac{\overrightarrow{AF}}{\overrightarrow{BF}}=-1\),说明分点D、E和F至少一点在对应线段内

dlsh

如图：ABC是等腰三角形，DB：DC=FA:FC，求证：△AFC相似CDB

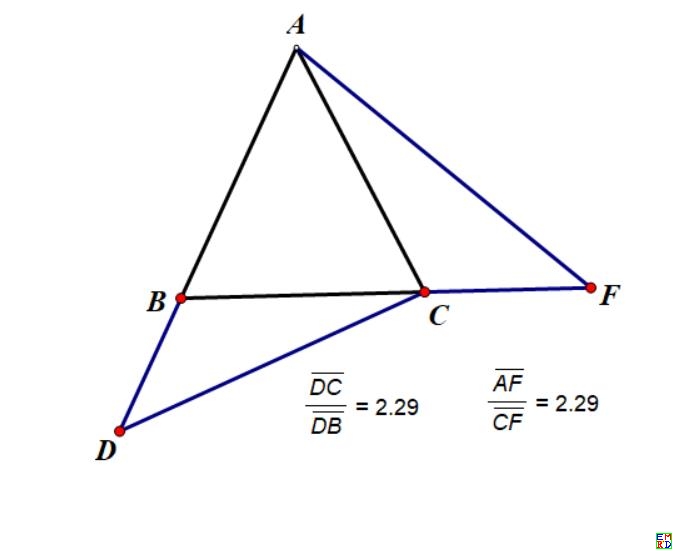
1. 假设e^iA = v
   
2. \!\(\*OverscriptBox["b", "_"]\) = b = 0;
   
3. \!\(\*OverscriptBox["c", "_"]\) = c = 1;
   
4. Fendian[a_, b_, u_] := (a - b u)/(1 - u);
   
5. \!\(\*OverscriptBox["Fendian", "_"]\)[a_, b_, u_] := (
   
6. \!\(\*OverscriptBox["a", "_"]\) -
   
7. \!\(\*OverscriptBox[
   
8. RowBox[{" ", "b", " "}], "_"]\)
   
9. \!\(\*OverscriptBox["u", "_"]\))/(1 -
   
10. \!\(\*OverscriptBox["u", "_"]\));(*向量定比分点公式,
    
11. \!\(\*OverscriptBox["Fendian", "_"]\)[a_,b_,u_]:=(
    
12. \!\(\*OverscriptBox["a", "_"]\)-
    
13. \!\(\*OverscriptBox[
    
14. RowBox[{" ", "b", " "}], "_"]\))/(u-1);!!*)
    
15. (*g=Fendian[c,b,v];
    
16. \!\(\*OverscriptBox["g", "_"]\)=
    
17. \!\(\*OverscriptBox["Fendian", "_"]\)[c,b,v];*)
    
18. a = 1/(1 - v);
    
19. \!\(\*OverscriptBox["a", "_"]\) = -(v/(1 - v));
    
20. (*d=Fendian[a,b,\[Lambda]];
    
21. \!\(\*OverscriptBox["d", "_"]\)=
    
22. \!\(\*OverscriptBox["Fendian", "_"]\)[a,b,\[Lambda]];*)
    
23. d = \[Lambda] a;
    
24. \!\(\*OverscriptBox["d", "_"]\) = \[Lambda]
    
25. \!\(\*OverscriptBox["a", "_"]\);
    
26. u = d/(d - c);
    
27. \!\(\*OverscriptBox["u", "_"]\) =
    
28. \!\(\*OverscriptBox["d", "_"]\)/(
    
29. \!\(\*OverscriptBox["d", "_"]\) -
    
30. \!\(\*OverscriptBox["c", "_"]\));
    
31. u1 = d/(d - c) w;
    
32. \!\(\*OverscriptBox["u1", "_"]\) =
    
33. \!\(\*OverscriptBox["d", "_"]\)/((
    
34. \!\(\*OverscriptBox["d", "_"]\) -
    
35. \!\(\*OverscriptBox["c", "_"]\)) w);
    
36. e = Fendian[c, a, u];
    
37. \!\(\*OverscriptBox["e", "_"]\) =
    
38. \!\(\*OverscriptBox["Fendian", "_"]\)[c, a, u];
    
39. e1 = Fendian[c, a, u1];
    
40. \!\(\*OverscriptBox["e1", "_"]\) =
    
41. \!\(\*OverscriptBox["Fendian", "_"]\)[c, a, u1];
    
42. Simplify[{d,
    
43. \!\(\*OverscriptBox["d", "_"]\), , e,
    
44. \!\(\*OverscriptBox["e", "_"]\), e -
    
45. \!\(\*OverscriptBox["e", "_"]\), e +
    
46. \!\(\*OverscriptBox["e", "_"]\)}]
    
47. Factor[e1 -
    
48. \!\(\*OverscriptBox["e1", "_"]\)]
    
49. Solve[e1 -
    
50. \!\(\*OverscriptBox["e1", "_"]\) == 0, w](*AE:CE=CD:BD=w*)

复制代码

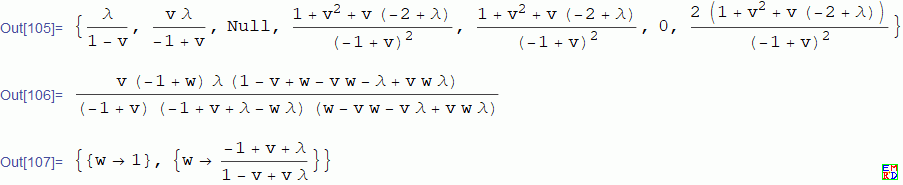
满足条件的点有两个，一个是要证明的结论，另外一个也很有意义，楼主的结论只是特例。

kastin

我记得德国数学家克莱因曾对几何学说过一句概括本质的话：几何是研究空间中运动不变量的学科。比如欧氏几何研究的各种比例面积体积共线等问题都可以总结为长度、角度关系，而它们在刚性旋转以及平移运动下是不变量。恰好向量有长度和方向，符合这些运动特点，因此能用于几何问题。只是向量的方向表示不便，往往几何中是用直角坐标投影表示向量，导致斜率体现方向，然而这会导致在数值运算上出现无穷大斜率的问题，不太方便。其根源在于向量的数学表达。

考虑到自由向量的特征是长度和方向(从线性代数的角度来看，有没有长度和方向是无所谓的，只要矢量满足一定运算性质，如线性性质等即可)，自然会想到采用用极坐标表达，得到一个长度和和一个方向角的数值，而复数的定义就是幅角和模长，正好符合这一特点，于是很自然地就能想到用复数来表示几何中的向量。至于除法的定义，其实直接可以看成是复数的除法，或者乘以复数的逆而已。因为复数的除法就是模长相除，辐角角相减，其本质就是“向量商”这个运算。但它存在一个问题，同样一个复数表达的向量，根本无法区分向量是否发生了平移。因为长度和方向在平移变换下是不变的。这个距离必须引入点积和叉积(有的书中叫外积)才能确定，而复数是没有内积和外积运算的，向量的内积和外积运算又是基于直角坐标系的表达，所以复数只能引入共轭乘积产生点积和叉积，才能与复数在复平面上的定义相兼容。

实际上，矢量只是一个二元数，它是四元数以及这类特殊的超复数的特例，从四元数的乘法运算上，我们才发现点积和叉积本身就是四元数好几种乘法(点积、外积、叉积也叫奇积、偶积)中两种而已，而四元数也存在除法运算(跟复数倒数类似)。其实外积和叉积的概念子在很多书中没有统一，比如张量相关里面的外积可认为是张量积(Kroneker积)，两个矢量的外积就是得到并矢(二阶张量)的乘法运算，但在四元数中的外积又与矢量的并矢和叉积都不一样。

矢量分析是物理学家们从四元数的实用主义裁剪而得，最初是为了电动力学在三维空间的表达而产生。但麦克斯韦确认同哈密顿的四元数观点，觉得用四元数表述电磁物理现象更合适，但由于四元数当时的支持者不多，他采取了折衷方案，同时使用坐标和四元数表述他的麦克斯韦方程组。可惜的是，现在的教科书全都被矢量分析所占据了，人们能了解这些真相的不多了。唯一值得欣慰的是，克利福德在其基础上有了发展。

creasson

大漠孤烟 发表于 2021-10-11 19:14
个人感觉作者的方法很强大，还得花时间去学习，但是有些结论表示过于复杂了。究其原因，就像数列的通项公式 ...

我的一个写作目的，并非为了像传统几何那样，通过巧妙构思或辅助线解决问题，也不是为了产生尽量简短的代数表示结果，而是为了生成可读的机器证明。
另外，单独有一节会提到几何结论的自动发现，这使得可以通过程序批量生成简洁的结果。

dlsh

错误的假设

上面假设Re (z2) < 0, Re (z3) < 0明显错误，比如有向角BDC和CDA等于-30度时，另外Re (z1) > 0当A是钝角时也是错误的。没必要这种假设，BC上满足线段比例的点有两个，是否在延长上需要单独讨论。

creasson

dlsh 发表于 2021-10-12 22:14
上面假设Re (z2) < 0, Re (z3) < 0明显错误，比如有向角BDC和CDA等于-30度时，另外Re (z1) > 0当A是钝角 ...

感谢指出，确实是错了，条件应是
\[{\mathop{\rm Im}\nolimits} ({z_1}) > 0, \quad
{\mathop{\rm Im}\nolimits} ({z_2}) < 0, \quad
{\mathop{\rm Im}\nolimits} ({z_3}) < 0\]

dlsh

creasson 发表于 2021-10-12 22:21
感谢指出，确实是错了，条件应是
\[{\mathop{\rm Im}\nolimits} ({z_1}) > 0, \quad
{\mathop{\rm Im}\ ...

这种假设只能证明其中一种情形，范围较小，书中的结论可以扩展，前面我的构图方式和程序包含这些情况。

反方向