用Mathematica编程求出最大误差函数值时如：10⁻⁸下的(x,a,b,c,d)

Jack315

【拟合迭代过程】
函数定义：

1. f0[x_] := Hypergeometric2F1[-(1/2), -(1/2), 1, x^2]
   
2. f1[x_, {a_, b_, c_}] := a + b x + c x^2

复制代码

初次拟合：

1. f1Param = Solve[Table[
   
2.     Table[SeriesCoefficient[f0[x], {x, 0.5, n}], {n, 0, 2}] ==
   
3.      Table[SeriesCoefficient[f1[x, {a, b, c}], {x, 0.5, n}], {n, 0, 2}]
   
4.     , {i, 3}], {a, b, c}][[1]]
   

复制代码

修正拟合使定义域两端误差为零：

1. f1k = ((f0[1] - f0[0])/(f1[1, {a, b, c}] - f1[0, {a, b, c}])) /. f1Param
   
2. f1b = Mean[{f0[0] - f1k f1[0, {a, b, c}], f0[0] - f1k f1[0, {a, b, c}]}] /. f1Param
   
3. f1[x_] := Table[x^(i - 1), {i, 3}].Table[f1Param[[i]][[2]], {i, 3}] f1k + f1b //Simplify

复制代码

误差函数：

1. err1[x_] := f0[x] - f1[x]
   
2. Plot[err1[x], {x, 0, 1},
   
3. PlotStyle -> Red,
   
4. Filling -> Axis,
   
5. GridLines -> Automatic,
   
6. Frame -> True,
   
7. PlotLabel -> "f1(x) 的拟合误差"]

复制代码

误差函数的三个零点：

1. sol = FindRoot[err1[x], {x, 0.5}]
   
2. x0s = {0, sol[[1]][[2]], 1}
   
3. Plot[err1[x], {x, 0, 1},
   
4. PlotStyle -> Red,
   
5. Filling -> Axis,
   
6. Epilog -> {PointSize[0.03], Table[Point[{x0s[[i]], 0}], {i, Length[x0s]}]},
   
7. GridLines -> Automatic,
   
8. Frame -> True,
   
9. PlotLabel -> "误差函数 err1(x) 的零点"]

复制代码

零点间的极值点：

1. xms = {x /. FindRoot[D[err1[x], x], {x, Mean[x0s[[1 ;; 2]]]}],
   
2.   x /. FindRoot[D[err1[x], x], {x, Mean[x0s[[2 ;; 3]]]}]}
   
3. yms = err1[x] /. x -> xms
   
4. Plot[err1[x], {x, 0, 1},
   
5. PlotStyle -> Red,
   
6. Filling -> Axis,
   
7. Epilog -> {PointSize[0.03],
   
8.    Table[Point[{xms[[i]], yms[[i]]}], {i, Length[xms]}]},
   
9. GridLines -> Automatic,
   
10. Frame -> True,
    
11. PlotLabel -> "误差函数 err1(x) 的极值点"]

复制代码

拟合左侧的峰：

1. f2[x_, {a_, b_, c_}] := a + b x + c x^2
   
2. f2Param = Solve[Table[
   
3.     Table[SeriesCoefficient[err1[x], {x, xms[[1]], n}], {n, 0, 2}] ==
   
4.      Table[SeriesCoefficient[f2[x, {a, b, c}], {x, xms[[1]], n}], {n, 0, 2}]
   
5.     , {i, 3}], {a, b, c}][[1]]
   
6. Plot[{err1[x], f2[x, {a, b, c}] /. f2Param}, {x, 0, 1},
   
7. Filling -> {1 -> {2}},
   
8. GridLines -> Automatic,
   
9. PlotLegends -> "Expressions",
   
10. Frame -> True,
    
11. PlotLabel -> "拟合函数 f2(x)"]

复制代码

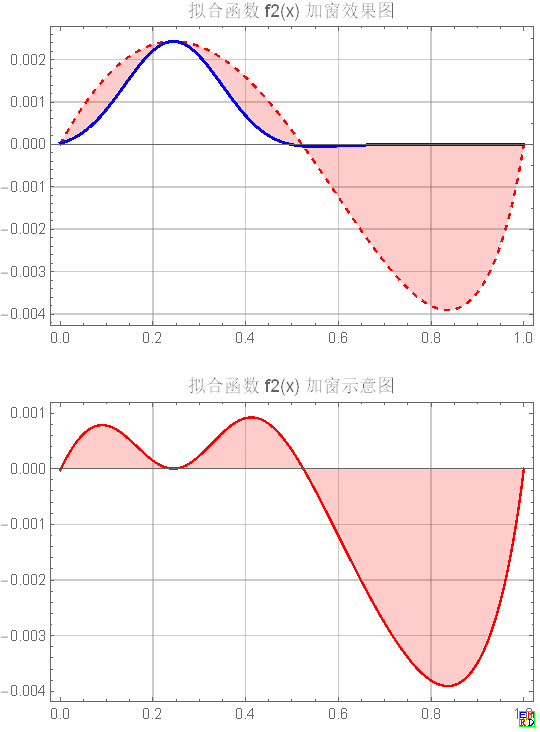
窗函数：

1. fwin[x_, {m_, s_}] := E^-((x - m)/s)^2
   
2. (*计算窗函数参数 s 的公式，w 是相邻零点的宽度*)
   
3. winS[w_] := w/3
   

复制代码

接下来是通过加窗函数逐个拟合误差函数的极值点……
代码改乱了，上个图看看加窗拟合的效果：

Jack315

迭代过程每次都拟合最大极值点的峰。
拟合的方法与 103# 相比作了改进：
保证极值点成为新的零点的条件下，最小化区间 [0,1] 两端点的误差平方和。
这样不至于因为不断的迭代而使这两个点的误差增加。

如果最终最大误差出现在区间端点，
则用一直线进行拟合，就可以把两个端点的误差重新拉回到零。
在迭代过程中这两点其实是伪零点，
将其作为零点处理，可以方便代码的设计。

这就是用加窗实现分段拟合的方法，
因此可以达到任意想要的拟合精度。
只是拟合函数的项数会特别多（有限项），
不似 LZ 的 \(\varphi(x)\) 函数那般精巧，有点“暴(xi)力(tong)”的感觉。

如果窗函数更方，而不再是这般油头滑脚的，
相信拟合会更精确、迭代能更快地达到所需的精度，
即更短的拟合函数项。

进行迭代的代码设计差不多了，还需要点时间进行调试。
另外也要使用更方的窗函数……希望这次能成功了。

笨笨

elim 发表于 2023-9-9 23:28
还没适应本论坛的 MathJax 设置。所以贴个图：

然后呢？没下文啦？？？

elim

笨笨 发表于 2023-9-11 20:44
然后呢？没下文啦？？？

笨笨可不是一般的笨，而是刻意不动脑子不学习不动手的笨．

@Jack315 :  建议用切比雪夫理论一举得到支集区间上凸/凹函数\(\tau/\|\tau\|_{\infty}\)的最隹多项式一致通近(\(\|\;\|_{\infty}\le 10^{-5}\)).
这样综合起来的误差就控制在e-12.

Jack315

elim 发表于 2023-9-12 00:12
笨笨可不是一般的笨，而是刻意不动脑子不学习不动手的笨．

@Jack315 :  建议用切比雪夫理论一举得到支集 ...

感谢前辈指导。切比雪夫理论的思路挺不错的，回头试试。
笨笨笨得可爱，这个题搞明白了啥意思其实不难，正好练习下编程。
笨笨其实不笨，光看这补偿函数就不简单，只是思路不一样，会有天花板。
赠人玫瑰，手留余香

笨笨

elim 发表于 2023-9-12 00:12
笨笨可不是一般的笨，而是刻意不动脑子不学习不动手的笨．

@Jack315 :  建议用切比雪夫理论一举得到支集 ...

前辈你好，按照这个思路走，可否给个具体实例来？？？？

笨笨

我就纳闷了，对拉马努金公式再拟合，一个函数族且误差达到10^-12就不能搞定？？？

Jack315

笨笨 发表于 2023-9-13 22:01
前辈你好，按照这个思路走，可否给个具体实例来？？？？

拟合函数：\(\lambda_0+\lambda_1x+\lambda_2x^2\)
窗函数为：\(\frac{1}{2tan^{-1}(\frac{b-a}{2}k)}\big(tan^{-1}[k(x-a)]-tan^{-1}[k(x-b)]\big)\)

代码已初步实现，有两个方面的难点：
1. 精确计算误差函数的零点和极值点，难在零点的计算上。
2. 拟合中相关数据较多，需要进行数据组织。

这是最新的调试状态，设置的精度要求为 1E-4，纯手工迭代：

蓝色点为零点；红色点为极值点；
青色点为待拟合点；黄色点为加窗边界点。
注：代码中，定义域端点 [0,1] 同时作为零点和极值点处理。
这是编程的需要，不是数学上的含义。

从图上可以看到漏了一个零点，加窗出错了。

要不要我把代码发上来，让高人来调试？
俺是超级业余的，数学和编程都不专业，就是爱玩这个东东。

笨笨

Jack315 发表于 2023-9-14 09:51
拟合函数：\(\lambda_0+\lambda_1x+\lambda_2x^2\)
窗函数为：\(\frac{1}{2tan^{-1}(\frac{b-a}{2}k)}\bi ...

代码不是楼主专业，若代码有疑问，请把代码发出来，看看路过的高手能不能解决一下？

笨笨

elim 发表于 2023-9-12 00:12
笨笨可不是一般的笨，而是刻意不动脑子不学习不动手的笨．

@Jack315 :  建议用切比雪夫理论一举得到支集 ...

elim老师自己说的方案，可能自己都实现不了？或者只是一种猜想。每次回帖都是留下一句话，然后就没有然后了，要是能给个具体实例分析一下就好了。可惜了，出于尊重，楼主持保留意见。