椭圆台曲面被斜截面截交的曲线求解

数学星空

我试着将Huxley与苏老的解法对比了一下，不知道下面推导是否有误？

\(|r|=\sqrt{x(t)^2+y(t)^2+z(t)^2}=\sqrt{r\*r}\)

\(d|r|=\frac{xdx+ydy+zdz}{|r|}=\frac{r\*r'}{|r|}\)

\(ds=\sqrt{(dx)^2+(dy)^2+(dz)^2}=\sqrt{r'\*r'}\)

\(d\theta=\frac{\sqrt{(ds)^2-(d|r|)^2}}{|r|}=\sqrt{(\frac{ds}{|r|})^2-(\frac{d|r|}{|r|})^2}=\sqrt{\frac{r'\*r'}{r\*r}-(\frac{r\*r'}{r\*r})^2}\)

对于偏心的一般椭圆锥可以得到极径及极角计算公式

\(x(t)=\lambda(a\cos(t)+x_0)\)

\(y(t)=\lambda(b\sin(t)+y_0)\)

\(z(t)=\lambda c\)

\(r=\lambda \sqrt{(a\cos(t)+x_0)^2+(b\sin(t)+y_0)^2+c^2}\)

\(\theta=\int_0^t\sqrt{\frac{a^2\sin(t)^2+b^2\cos(t)^2}{(a\cos(t)+x_0)^2+(b\sin(t)+y_0)^2+c^2}-(\frac{(b^2-a^2)\sin(t)\cos(t)+(by_0\cos(t)-ax_0\sin(t))}{(a\cos(t)+x_0)^2+(b\sin(t)+y_0)^2+c^2})^2} \dif t\)

Jack315

偏心椭圆锥展开曲线公式推导。

椭圆锥底面椭圆的参数方程：
\(x(\varphi)=\lambda(a\cos\varphi+x_0)\)
\(y(\varphi)=\lambda(b\sin\varphi+y_0)\)
\(z(\varphi)=\lambda h\)
其中：
\(a\) —— 椭圆锥底面椭圆长轴。
\(b\) —— 椭圆锥底面椭圆短轴。
\(h\) —— 椭圆锥高。
\(\lambda\) —— 比例参数，\(0\le\lambda\le1\) 。
\(\varphi\) —— 参变量，\(0\le\varphi\le2\pi\) 。

极径及其微分：
\(r(\varphi)=\sqrt{x^2(\varphi)+y^2(\varphi)+z^2(\varphi)}\)
\(r=\lambda\sqrt{(a\cos\varphi+x_0)^2+(b\sin\varphi+y_0)^2+h^2}\)
\(dr=\lambda\frac{-a\sin\varphi(a\cos\varphi+x_0)+b\cos\varphi(b\sin\varphi+y_0)}{\sqrt{(a\cos\varphi+x_0)^2+(b\sin\varphi+y_0)^2+h^2}}d\varphi\)
\(=\lambda\frac{(b^2-a^2)\sin\varphi\cos\varphi+by_0\cos\varphi-ax_0\sin\varphi}{\sqrt{(a\cos\varphi+x_0)^2+(b\sin\varphi+y_0)^2+h^2}}d\varphi\)

弧长相等：
\(dx=-\lambda a\sin\varphi\)
\(dy=\lambda b\cos\varphi\)
\(dz=0\)
\(ds=\lambda\sqrt{a^2\sin^2\varphi+b^2\cos^2\varphi}d\varphi=\sqrt{(dr)^2+(rd\theta)^2}\)

极角微分：
\(d\theta=\frac{1}{r}\sqrt{(ds)^2-(dr)^2}\)
\(=\frac{1}{r}\sqrt{\lambda^2(a^2\sin^2\varphi+b^2\cos^2\varphi)-\lambda^2\frac{[(b^2-a^2)\sin\varphi\cos\varphi+by_0\cos\varphi-ax_0\sin\varphi]^2}{(a\cos\varphi+x_0)^2+(b\sin\varphi+y_0)^2+h^2}}d\varphi\)
\(=\sqrt{\frac{a^2\sin^2\varphi+b^2\cos^2\varphi}{(a\cos\varphi+x_0)^2+(b\sin\varphi+y_0)^2+h^2}-[\frac{(b^2-a^2)\sin\varphi\cos\varphi+by_0\cos\varphi-ax_0\sin\varphi}{(a\cos\varphi+x_0)^2+(b\sin\varphi+y_0)^2+h^2}]^2}d\varphi\)

极角积分公式：
\(\theta=\int_0^\varphi\sqrt{\frac{a^2\sin^2\varphi+b^2\cos^2\varphi}{(a\cos\varphi+x_0)^2+(b\sin\varphi+y_0)^2+h^2}-[\frac{(b^2-a^2)\sin\varphi\cos\varphi+by_0\cos\varphi-ax_0\sin\varphi}{(a\cos\varphi+x_0)^2+(b\sin\varphi+y_0)^2+h^2}]^2}d\varphi\)

和 LZ 的结果相同。

Jack315

【平面与偏心椭圆锥体曲面交线】

偏心椭圆锥体曲面参数方程：
\(x(\varphi)=\lambda(a\cos\varphi+x_0)\)
\(y(\varphi)=\lambda(b\sin\varphi+y_0)\)
\(z(\varphi)=\lambda h\)
其中：
\(a\) —— 椭圆锥底面椭圆长轴。
\(b\) —— 椭圆锥底面椭圆短轴。
\(h\) —— 椭圆锥高。
\(\lambda\) —— 比例参数，\(0\le\lambda\le1\) 。
\(\varphi\) —— 参变量，\(0\le\varphi\le2\pi\) 。

取过点 \((x_p,y_p,z_p)\) 且法向量为 \(\overrightarrow{n}=(n_x,n_y,n_z)^T\) 的平面：
\([x(\varphi)-x_p,y(\varphi)-y_p,z(\varphi)-z_p]\cdot(n_x,n_y,n_z)=0\)
\([\lambda(a\cos\varphi+x_0)-x_p,\lambda(b\sin\varphi+y_0)-y_p,\lambda h-z_p]\cdot(n_x,n_y,n_z)=0\)
\(\lambda(\varphi)=\frac{n_xx_p+n_yy_p+n_zz_p}{n_x(a\cos\varphi+x_0)+n_y(b\sin\varphi+y_0)+n_zh}\)

平面与偏心椭圆锥体曲面的交线参数方程：
\(x(\varphi)=\frac{n_xx_p+n_yy_p+n_zz_p}{n_x(a\cos\varphi+x_0)+n_y(b\sin\varphi+y_0)+n_zh}(a\cos\varphi+x_0)\)
\(y(\varphi)=\frac{n_xx_p+n_yy_p+n_zz_p}{n_x(a\cos\varphi+x_0)+n_y(b\sin\varphi+y_0)+n_zh}(b\sin\varphi+y_0)\)
\(z(\varphi)=\frac{n_xx_p+n_yy_p+n_zz_p}{n_x(a\cos\varphi+x_0)+n_y(b\sin\varphi+y_0)+n_zh}h\)
其中：\(\varphi\) 为参变量，\(0\le\varphi\le2\pi\) 。

数学星空

若偏心椭圆台的上下椭圆长短轴长分别为\(a_1,b_1;a_2,b_2\),且上下椭圆面高度为\(h\),上下椭圆中心偏距\(x_0,y_0\)
那这个偏心椭圆台的曲面方程怎么算？
现从上椭圆面右端斜切至距下椭圆面左端高度为\(h_0\)处，这个截交曲线是什么？

Jack315

椭圆台曲面参数方程：
\(x(\varphi)=[\lambda a_1+(1-\lambda)a_2]\cos\varphi+[\lambda x_{10}+(1-\lambda)x_{20}]\)
\(y(\varphi)=[\lambda b_1+(1-\lambda)b_2]\sin\varphi+[\lambda y_{10}+(1-\lambda)y_{20}]\)
\(z(\varphi)=\lambda h_1+(1-\lambda)h_2\)

其中：
\(a_1\) —— 上椭圆长轴。
\(b_1\) —— 上椭圆短轴。
\(h_1\) —— 上椭圆高。
\(x_{10}\) —— 上椭圆中心横坐标。
\(y_{10}\) —— 上椭圆中心纵坐标。

\(a_2\) —— 下椭圆长轴。
\(b_2\) —— 下椭圆短轴。
\(h_2\) —— 下椭圆高。
\(x_{20}\) —— 下椭圆中心横坐标。
\(y_{20}\) —— 下椭圆中心纵坐标。

\(\lambda\) —— 比例参数，\(0\le\lambda\le1\) 。
\(\varphi\) —— 参变量，\(0\le\varphi\le2\pi\) 。



LZ 看看是不是这样的椭圆台面。

Jack315

数学星空 发表于 2024-4-2 08:07
若偏心椭圆台的上下椭圆长短轴长分别为\(a_1,b_1;a_2,b_2\),且上下椭圆面高度为\(h\),上下椭圆中心偏距\(x_ ...

【平面与椭圆台曲面截交线】

椭圆台曲面参数方程：
\(x(\varphi)=[\lambda a_1+(1-\lambda)a_2]\cos\varphi+[\lambda x_{10}+(1-\lambda)x_{20}]\)
\(y(\varphi)=[\lambda b_1+(1-\lambda)b_2]\sin\varphi+[\lambda y_{10}+(1-\lambda)y_{20}]\)
\(z(\varphi)=\lambda h_1+(1-\lambda)h_2\)

其中：
\(a_1\) —— 上椭圆长轴。
\(b_1\) —— 上椭圆短轴。
\(h_1\) —— 上椭圆高。
\(x_{10}\) —— 上椭圆中心横坐标。
\(y_{10}\) —— 上椭圆中心纵坐标。

\(a_2\) —— 下椭圆长轴。
\(b_2\) —— 下椭圆短轴。
\(h_2\) —— 下椭圆高。
\(x_{20}\) —— 下椭圆中心横坐标。
\(y_{20}\) —— 下椭圆中心纵坐标。

\(\lambda\) —— 比例参数，\(0\le\lambda\le1\) 。
\(\varphi\) —— 参变量，\(0\le\varphi\le2\pi\) 。

取过点 \((x_p,y_p,z_p)\)  且法向量为 \(\overrightarrow{n}=(n_x,n_y,n_z)^T\) 的平面：
\([x(\varphi)-x_p,y(\varphi)-y_p,z(\varphi)-z_p]\cdot(n_x,n_y,n_z)=0\)

\(\{[\lambda a_1+(1-\lambda)a_2]\cos\varphi+[\lambda x_{10}+(1-\lambda)x_{20}]-x_p,\)
\([\lambda b_1+(1-\lambda)b_2]\sin\varphi+[\lambda y_{10}+(1-\lambda)y_{20}]-y_p,\)
\(\lambda h_1+(1-\lambda)h_2-z_p\}\cdot(n_x,n_y,n_z)=0\)

\(\lambda(\varphi)=\frac{(x_{20}-x_p,y_{20}-y_p,h_2-z_p)\cdot(n_x,n_y,n_z)+(a_2,b_2)\cdot(n_a,n_y)\cos\varphi}
{(x_{20}-x_{10},y_{20}-y_{10},h_2-h_1)\cdot(n_x,n_y,n_z)+(a_2-a_1,b_2-b_1)\cdot(n_x,n_y)\cos\varphi}\)

把 \(\lambda(\varphi)\) 代入 椭圆台曲面参数方程即得截交线的参数方程。式子有点长 。

Jack315

Jack315 发表于 2024-4-2 11:16
椭圆台曲面参数方程：
\(x(\varphi)=[\lambda a_1+(1-\lambda)a_2]\cos\varphi+[\lambda x_{10}+(1-\lambda ...

令 \(a_1=0\) 得椭圆锥曲面：

数学星空

参照43#的参数形式，为了使圆锥翻转成上小下大的椭圆台，我们设

\(x(t)=k(a_2\cos(t)+x_2)\)

\(y(t)=k(b_2\sin(t)+y_2)\)

\(z(t)=(1-k)H\)

根据44#的参数要求，当\(z(t)=h\) 时

\(k=1-\frac{h}{H},a_1=(1-\frac{h}{H})a_2,x_1=(1-\frac{h}{H})x_2,b_1=(1-\frac{h}{H})b_2,y_1=(1-\frac{h}{H})y_2\)

显然上面已包含关系\(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)，这个是上下椭圆共圆锥曲面的必要条件吗？？？

又因上下椭圆偏心距为\(x_0,y_0\),即有

\(y_2-y_1=y_0,x_2-x_1=x_0\)

代入求得：

\(H=\frac{a_2h}{a_2-a_1},x_1=\frac{x_0a_1}{a_2-a_1},x_2=\frac{x_0a_2}{a_2-a_1},y_1=\frac{y_0a_1}{a_2-a_1},y_2=\frac{y_0a_2}{a_2-a_1}\)

上椭圆右端点\(k=1-\frac{h}{H},t=0\)得到坐标点\(A[x=\frac{(H-h)(a_2+x_2)}{H},y=\frac{(H-h)y_2}{H},z=h]\)

下椭圆左端点距底\(h_0\)处点\(k=1-\frac{h_0}{H},t=\pi\),得到坐标点\(B[x=-\frac{(H-h_0)(a_2-x_2)}{H},y=\frac{(H-h_0)y_2}{H},z=h_0]\)

由A,B两点得到斜切面方程：

\((a_1h^2 -a_1hh_0 - a_2h^2 + a_2hh_0)x + (-a_1^2h -a_1^2h_0 + 2a_1a_2h_0 +a_1hx_0 -a_1h_0x_0 + a_2^2h - a_2^2h_0 - a_2hx_0 + a_2h_0x_0)z + 2a_1^2hh_0 +a_1a_2h^2 - 3a_1a_2hh_0 - a_2^2h^2 + a_2^2hh_0 + a_2h^2x_0 - a_2hh_0x_0=0\)

斜面截交曲线方程：

\(x=k_0 (a_2\cos(t)-\frac{x_0a_2}{a_1-a_2})\)
\(y=k_0( b_2\sin(t)-\frac{y_0a_2}{a_1-a_2})\)
\(z=-\frac{(1-k_0)a_2h}{a_1-a_2}\)

\(k_0=-\frac{2a_1(h_0a_1+a_2h-h_0a_2)}{a_2(\cos(t)(ha_1-h_0a_1-a_2h+h_0a_2)-ha_1-h_0a_1-a_2h+h_0a_2)}\)

例如：取

\(a_1=50,b_1=80,a_2=100,b_2=150,h=100,x_0=10,y_0=40,h_0=10\)

算得

\(H=200,x_1=10,x_2=20,y_1=40,y_2=80\)

斜切面方程：\(z=\frac{45x}{68}+\frac{1025}{17}\)

斜面截交曲线方程：

\(x=\frac{380*(5\cos(t) + 1)}{9\cos(t) + 29}, y =\frac{190*(15\sin(t) + 8)}{9\cos(t) + 29}, z=\frac{200*(9\cos(t) + 10)}{9\cos(t) + 29}\)

斜面截交曲线方程(隐函数方程):

(a1^2*b2^2*h^2 - 2*a1*a2*b2^2*h^2 + a2^2*b2^2*h^2)*x^2 + ((2*a1^2*b2^2*h*x0 - 4*a1*a2*b2^2*h*x0 + 2*a2^2*b2^2*h*x0)*z + 2*a1*a2*b2^2*h^2*x0 - 2*a2^2*b2^2*h^2*x0)*x + (a1^2*a2^2*h^2 - 2*a1*a2^3*h^2 + a2^4*h^2)*y^2 + ((2*a1^2*a2^2*h*y0 - 4*a1*a2^3*h*y0 + 2*a2^4*h*y0)*z + 2*y0*a2^3*a1*h^2 - 2*a2^4*h^2*y0)*y + (-a1^4*b2^2 + 4*a1^3*a2*b2^2 - 6*a1^2*a2^2*b2^2 + a1^2*a2^2*y0^2 + a1^2*b2^2*x0^2 + 4*a1*a2^3*b2^2 - 2*a1*a2^3*y0^2 - 2*a1*a2*b2^2*x0^2 - a2^4*b2^2 + a2^4*y0^2 + a2^2*b2^2*x0^2)*z^2 + (-2*a1^3*a2*b2^2*h + 6*a1^2*a2^2*b2^2*h - 6*a1*a2^3*b2^2*h + 2*a1*a2^3*h*y0^2 + 2*a1*a2*b2^2*h*x0^2 + 2*a2^4*b2^2*h - 2*a2^4*h*y0^2 - 2*a2^2*b2^2*h*x0^2)*z - a1^2*a2^2*b2^2*h^2 + 2*a1*a2^3*b2^2*h^2 - a2^4*b2^2*h^2 + a2^4*h^2*y0^2 + a2^2*b2^2*h^2*x0^2=0

代入参数得到：

\(x^2 +\frac{1}{5}zx + \frac{4}{9}y^2 + \frac{16}{45}zy - \frac{38}{225}z^2 - 40x - \frac{640}{9}y + \frac{608}{9}z - \frac{60800}{9}=0\)

画图得到的都很完美！！





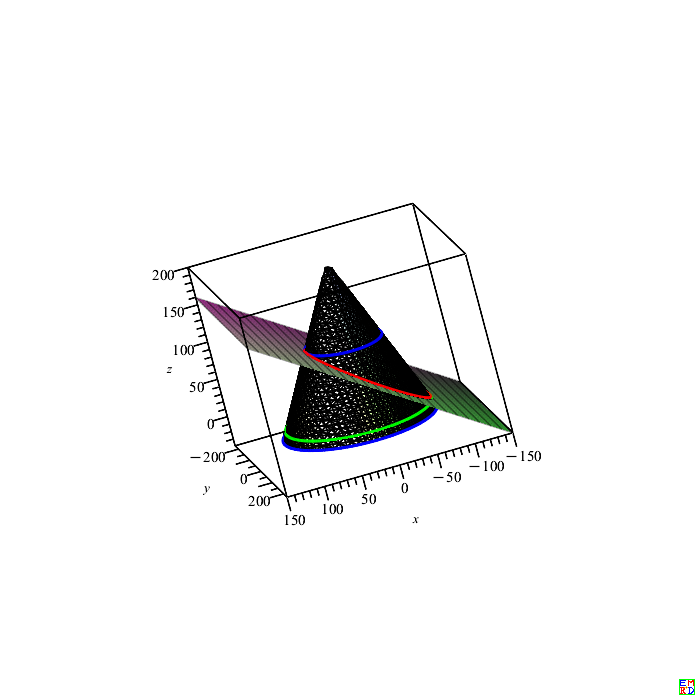
还一个问题就是：关系\(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)，这个是上下椭圆共圆锥曲面的必要条件吗？？？(本例参数\(a_1=50,b_1=80,a_2=100,b_2=150,h=100,x_0=10,y_0=40,h_0=10\) 并不满足此条件）

Jack315

这是我推导椭圆台曲面参数方程的过程，供参考。

椭圆台上椭圆参数方程：
\(x=a_1\cos\varphi+x_{10}\)
\(y=b_1\sin\varphi+y_{10}\)
\(z=h_1\)

椭圆台下椭圆参数方程：
\(x=a_2\cos\varphi+x_{20}\)
\(y=b_2\sin\varphi+y_{20}\)
\(z=h_2\)

各参数取相同的线性关系（中括号里的表达式）得椭圆台曲面参数方程：
\(x=[\lambda a_1+(1-\lambda)a_2]\cos\varphi+[\lambda x_{10}+(1-\lambda)x_{20}]\)
\(y=[\lambda b_1+(1-\lambda)b_2]\sin\varphi+[\lambda y_{10}+(1-\lambda)y_{20}]\)
\(z=[\lambda h_1+(1-\lambda)h_2]\)

\(0\le\lambda\le1\)，\(0\le\varphi\le2\pi\) 。

Jack315

到目前为止所讨论的空间曲线都是某个平面上的椭圆，而椭圆是圆锥曲线的一种。
因此这类斜椭圆锥体、椭圆平台……等与平面截交线展开的问题，
是不是可以通过三维空间的旋转、平移和缩放，转换为正圆锥体与某个平面交线的展开问题？

如果答案是肯定的，则只要研究正圆锥体与某个平面截交线展开这一个问题就可以了。
而相应的计算公式可能也会变得简洁得多。

更进一步地是否可以将正圆锥体定义成一个标准的圆锥体，如高和底面圆半径都为 1 的单位正圆锥体。
然后通过平移、旋转和缩放得到所需的（椭）圆锥体。

参考：三维空间中的几何变换-平移旋转缩放