椭圆台曲面被斜截面截交的曲线求解

数学星空

参照46#的参数形式，我们可以设椭圆台的曲面参数方程为

\(x(t)=(ka_1+(1-k)a_2)\cos(t)+(kx_1+(1-k)x_2)\)

\(y(t)=(kb_1+(1-k)b_2)\cos(t)+(ky_1+(1-k)y_2)\)

\(z(t)=kh\)

我们可以计算上椭圆右端点\(k=1,t=0\)得到坐标点\(A[x=a_1-x_0,y=-y_0,z=h]\)

下椭圆左端点距底\(h_0\)处点\(k=\frac{h_0}{h},t=\pi\),得到坐标点\(B[x=-(a_2+\frac{h_0(a_1-a_2)}{h}-\frac{h_0x_0}{h},y=-\frac{h_0y_0}{h},z=h_0]\)

由A,B两点得到斜切面方程：

\((h^2 - hh_0)x + (-a_1h - a_1h_0 - a_2h + a_2h_0 + hx_0 - h_0x_0)z + 2a_1hh_0 + a_2h^2 - a_2hh_0=0\)

斜面截交曲线方程：

\(x=(ka_1 + (1 - k)a_2)\cos(t) - kx_0\)

\(y=(kb_1 + (1 - k)b_2)\cos(t) - ky_0\)

\(z=kh\)

\(k=\frac{(a_2h - a_2h_0)\cos(t) + 2h_0a_1 + a_2h - a_2h_0}{(a_1h - a_1h_0 - a_2h + a_2h_0)\cos(t) - a_1h - h_0a_1 - a_2h + a_2h_0}\)

偏心椭圆台曲面的隐函数方程：

\(\frac{(xh+zx_0)^2}{(za_1+a_2h-a_2z)^2}+\frac{(yh+zy_0)^2}{(zb_1+b_2h-b_2z)^2}=1\)

由上面的极径和极角公式，我们可以计算得到：

例1：正椭圆台

\(a_1 = 50, a_2 = 80, b_1 = 100, b_2 = 150, h = 150, h_0 = 0, x_0 = 0, y_0 = 0\)

斜切平面方程：

\(z=\frac{15x}{16}+\frac{1200}{13}\)

截交曲线参数方程：

\(x = 800\frac{\cos(t)}{3\cos(t) + 13}\),
\(y = 50\frac{\cos(t) + 31}{\sin(t)(3\cos(t) + 13)}\),
\(z =1200\frac{\cos(t) + 1}{3\cos(t) + 13}\)

绘图

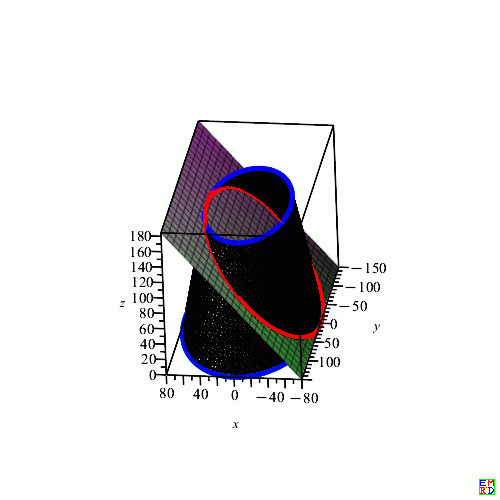
绘图

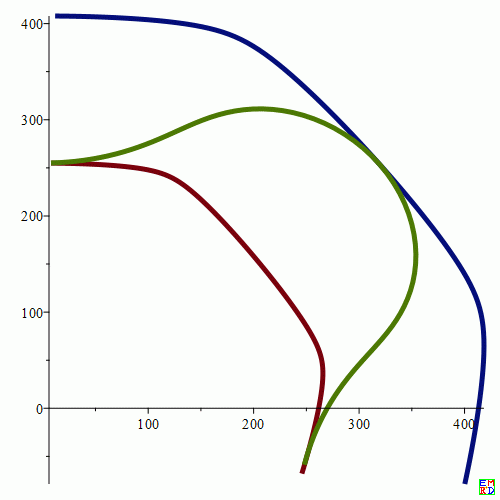
（中间的曲线为截交曲线展开曲线，内外两条曲线为椭圆台上下端面展开曲线）

绘图

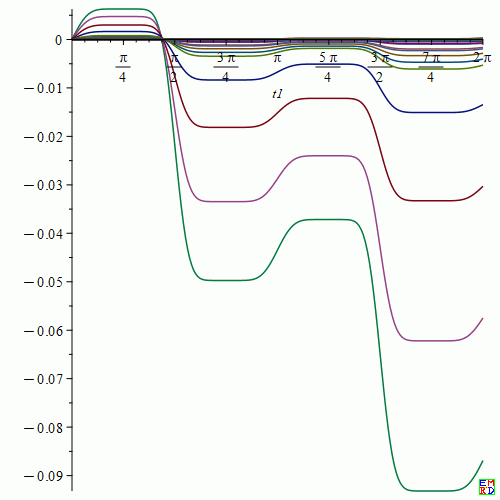
渐近分析展开得到的误差在 \([\pi,2\pi]\)区间误差较大，最大误差接近0.18度，可以勉强使用

渐近分析展开公式

，



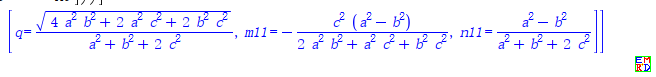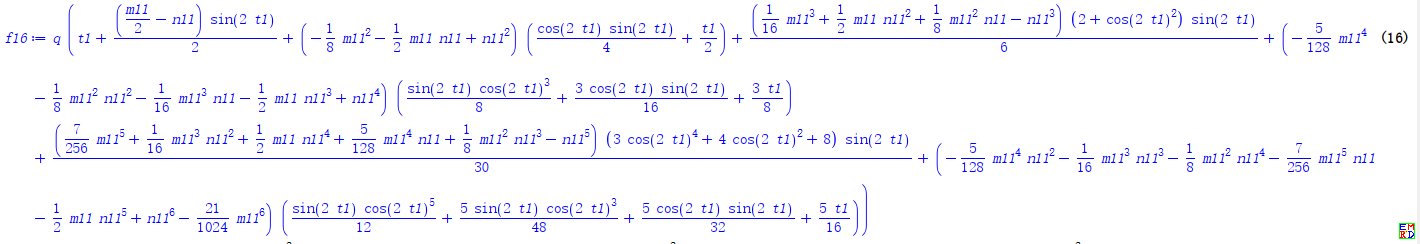
对于偏心椭圆台：

\(a_1=50,a_2=100,b_1=80,b_2=250,h=150,h_0=30,x_0=10,x_1=-10,x_2=0,y_0=50,y_1=-50,y_2=0\)

绘图

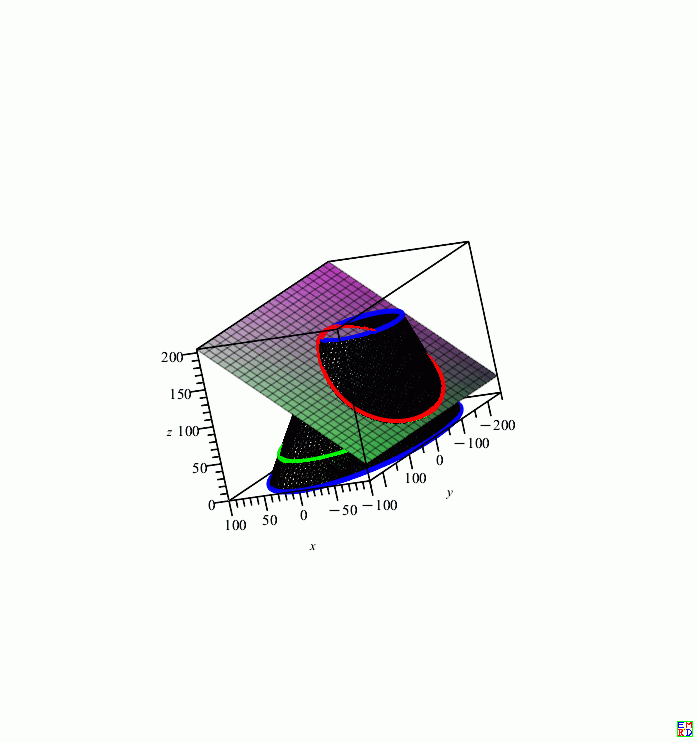
绘图

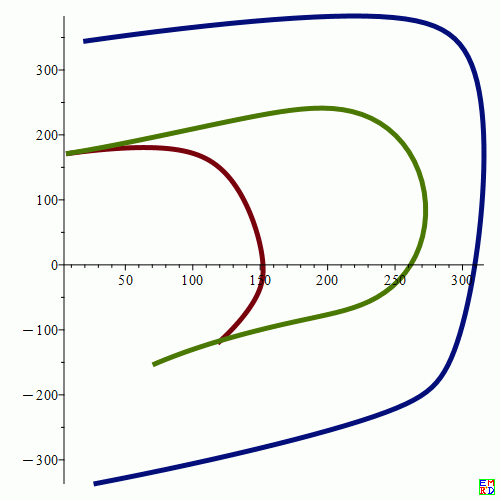
绘图

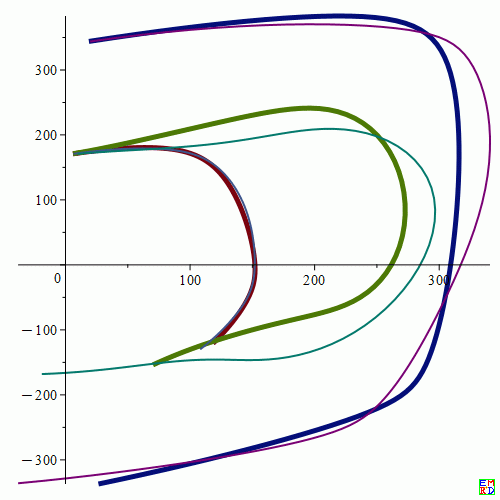
（细线部分为利用渐近展开计算得到结果，粗实线为理论数值计算的结果，明显已偏移，渐近展开方案已不适用偏心椭圆台的计算）


经过各种尝试，终于找到一种变结点权函数的计算公式（高斯-勒让德积分计算公式，适用于偏心椭圆台展开计算）

（1）若将整个 \([0,2\pi]\)分成4等份计算，最大误差为0.9887度
         

       计算公式见
      

（2)若将整个 \([0,2\pi]\)分成4*8=32等份计算，最大误差为10^(-3)度，足矣满足工程要求

        计算公式见
        

       其中\(g_k\)的脚标表示\(t=k\)时的函数取值