等边六边形三线共点猜想

hujunhua

由于3楼的那个解释，我仍然倾向于猜想不成立，虽然我任意画图，三条中点连线都高精度地共点重合。

如果猜想成立，就表明等边六边形不能仿射等价于一般六边形。这真的匪夷所思，难以想象。

nyy

hujunhua 发表于 2024-3-14 23:23
由于3楼的那个解释，我仍然倾向于猜想不成立，虽然我任意画图，三条中点连线都高精度地共点重合。

如果猜 ...

9楼不是有证明吗？难道九楼的证明不正确？

hujunhua

mathe 发表于 2024-3-14 13:11
以下用大写字母表示位置矢量，黑体小写字母表示自由向量。  
如图，设等边六边形`ABCDEF`的顶点`A`在原点 ...

证明过程并不限于平面向量，所以对三维空间也成立。
8#的例外应该跟`\boldsymbol a+\boldsymbol d=0`有关，这使得证明失效。
但是7#也存在`\boldsymbol a+\boldsymbol d=0`，所以例外的原因需要细究。

hujunhua

我对于9#的证明是抱有一定疑虑的，因为内积运算是不可逆的，所以方程变换不是等价变换。
也就是说通过变换计算出来的解代回原方程进行验算不一定能通过。
对于平面的情形，证明可行，因为交点的存在性有保障。三维空间存疑。

如图，若三线共于点M，那么有加强结论：GM·MJ=HM·MK=IM·ML.
按圆的相交弦定理，这个连等式意味着中点六边形GHIJKL中，任意两对相对顶点（四点）共圆。
比如GHJK四点所共圆的圆心就是FC（图上未画出，请脑补）的中点，记为N，因为
NG∥BC，并且NG=BC/2=a/2，同样，NH=FA/2=a/2，NJ=EF/2=a/2，NK=CD/2=a/2.
可见，所共圆的直径就是原等边六边形的边长，多么奇妙!

数学星空

为了方便计算，我们可以设等边六边形的边长为x,内接三角形ABC的边长分别为BC=a1,AC=b1,AB=c1
建立坐标系，B[0,0],C[a1,0],A[m,n],对于给定的a1=7,b1=5,c1=6,x=3.5+2*k/100 (k=1..100)
可以求出所有的100个等六边形及相应的胡心坐标，绘图得到



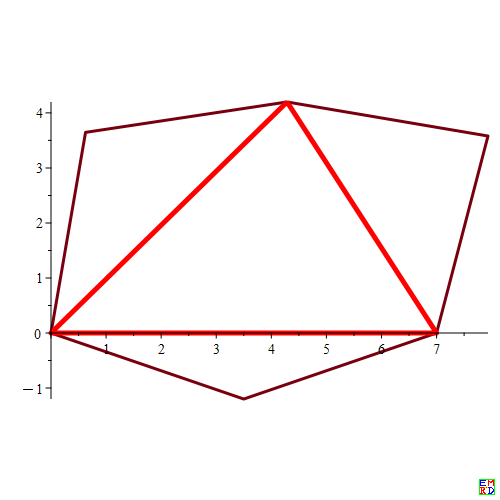
经过代数方程消元可以得到胡心(x0,y0)的轨迹方程（关于a1,b1,c1,x):
a1^10*c1^4 - 2*a1^9*b1^2*c1^2*x0 - 10*a1^9*c1^4*x0 + a1^8*b1^4*x0^2 + a1^8*b1^4*y0^2 + 18*a1^8*b1^2*c1^2*x0^2 - 18*a1^8*b1^2*c1^2*y0^2 - 2*a1^8*c1^6 + 41*a1^8*c1^4*x0^2 + 9*a1^8*c1^4*y0^2 + 2*a1^7*b1^4*c1^2*x0 - 8*a1^7*b1^4*x0^3 - 8*a1^7*b1^4*x0*y0^2 - 6*a1^7*b1^2*c1^4*x0 - 64*a1^7*b1^2*c1^2*x0^3 + 192*a1^7*b1^2*c1^2*x0*y0^2 + 20*a1^7*c1^6*x0 - 88*a1^7*c1^4*x0^3 - 56*a1^7*c1^4*x0*y0^2 - 2*a1^6*b1^6*x0^2 - 2*a1^6*b1^6*y0^2 - 10*a1^6*b1^4*c1^2*x0^2 + 26*a1^6*b1^4*c1^2*y0^2 + 24*a1^6*b1^4*x0^4 + 32*a1^6*b1^4*x0^2*y0^2 + 8*a1^6*b1^4*y0^4 + 46*a1^6*b1^2*c1^4*x0^2 - 46*a1^6*b1^2*c1^4*y0^2 + 112*a1^6*b1^2*c1^2*x0^4 - 672*a1^6*b1^2*c1^2*x0^2*y0^2 + 112*a1^6*b1^2*c1^2*y0^4 + a1^6*c1^8 - 82*a1^6*c1^6*x0^2 - 18*a1^6*c1^6*y0^2 + 104*a1^6*c1^4*x0^4 + 128*a1^6*c1^4*x0^2*y0^2 + 24*a1^6*c1^4*y0^4 + 16*a1^5*b1^6*x0^3 + 16*a1^5*b1^6*x0*y0^2 - 2*a1^5*b1^4*c1^4*x0 + 8*a1^5*b1^4*c1^2*x0^3 - 216*a1^5*b1^4*c1^2*x0*y0^2 - 32*a1^5*b1^4*x0^5 - 64*a1^5*b1^4*x0^3*y0^2 - 32*a1^5*b1^4*x0*y0^4 + 8*a1^5*b1^2*c1^6*x0 - 136*a1^5*b1^2*c1^4*x0^3 + 248*a1^5*b1^2*c1^4*x0*y0^2 - 96*a1^5*b1^2*c1^2*x0^5 + 960*a1^5*b1^2*c1^2*x0^3*y0^2 - 480*a1^5*b1^2*c1^2*x0*y0^4 - 10*a1^5*c1^8*x0 + 176*a1^5*c1^6*x0^3 + 112*a1^5*c1^6*x0*y0^2 - 64*a1^5*c1^4*x0^5 - 128*a1^5*c1^4*x0^3*y0^2 - 64*a1^5*c1^4*x0*y0^4 + a1^4*b1^8*x0^2 + a1^4*b1^8*y0^2 - 8*a1^4*b1^6*c1^2*x0^2 - 12*a1^4*b1^6*c1^2*y0^2 - 48*a1^4*b1^6*x0^4 - 64*a1^4*b1^6*x0^2*y0^2 - 16*a1^4*b1^6*y0^4 + 34*a1^4*b1^4*c1^4*x0^2 + 38*a1^4*b1^4*c1^4*y0^2 + 32*a1^4*b1^4*c1^2*x0^4 + 560*a1^4*b1^4*c1^2*x0^2*y0^2 - 48*a1^4*b1^4*c1^2*y0^4 + 16*a1^4*b1^4*x0^6 + 48*a1^4*b1^4*x0^4*y0^2 + 48*a1^4*b1^4*x0^2*y0^4 + 16*a1^4*b1^4*y0^6 - 64*a1^4*b1^2*c1^6*x0^2 - 36*a1^4*b1^2*c1^6*y0^2 + 192*a1^4*b1^2*c1^4*x0^4 - 400*a1^4*b1^2*c1^4*x0^2*y0^2 + 112*a1^4*b1^2*c1^4*y0^4 + 32*a1^4*b1^2*c1^2*x0^6 - 480*a1^4*b1^2*c1^2*x0^4*y0^2 + 480*a1^4*b1^2*c1^2*x0^2*y0^4 - 32*a1^4*b1^2*c1^2*y0^6 + 41*a1^4*c1^8*x0^2 + 9*a1^4*c1^8*y0^2 - 208*a1^4*c1^6*x0^4 - 256*a1^4*c1^6*x0^2*y0^2 - 48*a1^4*c1^6*y0^4 + 16*a1^4*c1^4*x0^6 + 48*a1^4*c1^4*x0^4*y0^2 + 48*a1^4*c1^4*x0^2*y0^4 + 16*a1^4*c1^4*y0^6 - 8*a1^3*b1^8*x0^3 - 8*a1^3*b1^8*x0*y0^2 + 56*a1^3*b1^6*c1^2*x0^3 + 88*a1^3*b1^6*c1^2*x0*y0^2 + 64*a1^3*b1^6*x0^5 + 128*a1^3*b1^6*x0^3*y0^2 + 64*a1^3*b1^6*x0*y0^4 - 160*a1^3*b1^4*c1^4*x0^3 - 224*a1^3*b1^4*c1^4*x0*y0^2 - 64*a1^3*b1^4*c1^2*x0^5 - 512*a1^3*b1^4*c1^2*x0^3*y0^2 + 64*a1^3*b1^4*c1^2*x0*y0^4 + 200*a1^3*b1^2*c1^6*x0^3 + 200*a1^3*b1^2*c1^6*x0*y0^2 - 128*a1^3*b1^2*c1^4*x0^5 + 128*a1^3*b1^2*c1^4*x0^3*y0^2 - 256*a1^3*b1^2*c1^4*x0*y0^4 - 88*a1^3*c1^8*x0^3 - 56*a1^3*c1^8*x0*y0^2 + 128*a1^3*c1^6*x0^5 + 256*a1^3*c1^6*x0^3*y0^2 + 128*a1^3*c1^6*x0*y0^4 + 24*a1^2*b1^8*x0^4 + 32*a1^2*b1^8*x0^2*y0^2 + 8*a1^2*b1^8*y0^4 - 144*a1^2*b1^6*c1^2*x0^4 - 240*a1^2*b1^6*c1^2*x0^2*y0^2 - 32*a1^2*b1^6*c1^2*y0^4 - 32*a1^2*b1^6*x0^6 - 96*a1^2*b1^6*x0^4*y0^2 - 96*a1^2*b1^6*x0^2*y0^4 - 32*a1^2*b1^6*y0^6 + 320*a1^2*b1^4*c1^4*x0^4 + 512*a1^2*b1^4*c1^4*x0^2*y0^2 + 64*a1^2*b1^4*c1^4*y0^4 + 32*a1^2*b1^4*c1^2*x0^6 + 96*a1^2*b1^4*c1^2*x0^4*y0^2 + 96*a1^2*b1^4*c1^2*x0^2*y0^4 + 32*a1^2*b1^4*c1^2*y0^6 - 304*a1^2*b1^2*c1^6*x0^4 - 432*a1^2*b1^2*c1^6*x0^2*y0^2 - 64*a1^2*b1^2*c1^6*y0^4 + 32*a1^2*b1^2*c1^4*x0^6 + 96*a1^2*b1^2*c1^4*x0^4*y0^2 + 96*a1^2*b1^2*c1^4*x0^2*y0^4 + 32*a1^2*b1^2*c1^4*y0^6 + 104*a1^2*c1^8*x0^4 + 128*a1^2*c1^8*x0^2*y0^2 + 24*a1^2*c1^8*y0^4 - 32*a1^2*c1^6*x0^6 - 96*a1^2*c1^6*x0^4*y0^2 - 96*a1^2*c1^6*x0^2*y0^4 - 32*a1^2*c1^6*y0^6 - 32*a1*b1^8*x0^5 - 64*a1*b1^8*x0^3*y0^2 - 32*a1*b1^8*x0*y0^4 + 160*a1*b1^6*c1^2*x0^5 + 320*a1*b1^6*c1^2*x0^3*y0^2 + 160*a1*b1^6*c1^2*x0*y0^4 - 288*a1*b1^4*c1^4*x0^5 - 576*a1*b1^4*c1^4*x0^3*y0^2 - 288*a1*b1^4*c1^4*x0*y0^4 + 224*a1*b1^2*c1^6*x0^5 + 448*a1*b1^2*c1^6*x0^3*y0^2 + 224*a1*b1^2*c1^6*x0*y0^4 - 64*a1*c1^8*x0^5 - 128*a1*c1^8*x0^3*y0^2 - 64*a1*c1^8*x0*y0^4 + 16*b1^8*x0^6 + 48*b1^8*x0^4*y0^2 + 48*b1^8*x0^2*y0^4 + 16*b1^8*y0^6 - 64*b1^6*c1^2*x0^6 - 192*b1^6*c1^2*x0^4*y0^2 - 192*b1^6*c1^2*x0^2*y0^4 - 64*b1^6*c1^2*y0^6 + 96*b1^4*c1^4*x0^6 + 288*b1^4*c1^4*x0^4*y0^2 + 288*b1^4*c1^4*x0^2*y0^4 + 96*b1^4*c1^4*y0^6 - 64*b1^2*c1^6*x0^6 - 192*b1^2*c1^6*x0^4*y0^2 - 192*b1^2*c1^6*x0^2*y0^4 - 64*b1^2*c1^6*y0^6 + 16*c1^8*x0^6 + 48*c1^8*x0^4*y0^2 + 48*c1^8*x0^2*y0^4 + 16*c1^8*y0^6=0

若a1=7,b1=5,c1=6代入可以得到：

131606784*x0^6 - 849858048*x0^4*y0^2 + 1224605952*x0^2*y0^4 - 6690816*y0^6 - 2721341952*x0^5 + 13286762496*x0^3*y0^2 - 8964490752*x0*y0^4 + 21420491904*x0^4 - 81064351872*x0^2*y0^2 + 16377709824*y0^4 - 79701302016*x0^3 + 225238583808*x0*y0^2 + 140773472784*x0^2 - 237434851584*y0^2 - 102883042080*x0 + 25767954576=0

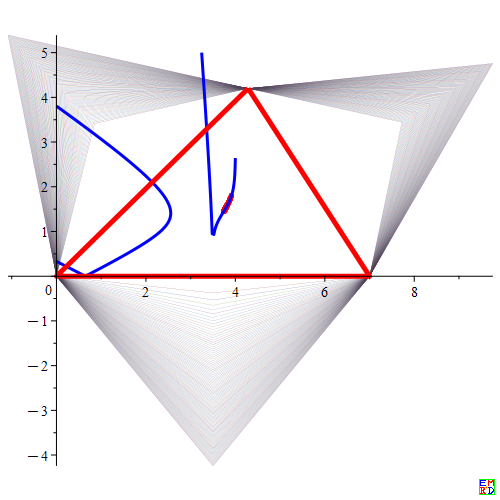
画图得到：（以下蓝色为胡心轨迹，红色三角形为ABC,红色点为100个样本等六边形胡心轨迹）
显然蓝色的胡心轨迹有两根，其中有红色样本点的应该是外凸等六边形的胡心轨迹，还有一根可能是内凹等六边形的胡心轨迹

数学星空

试着将下面方程继续分解
131606784*x0^6 - 849858048*x0^4*y0^2 + 1224605952*x0^2*y0^4 - 6690816*y0^6 - 2721341952*x0^5 + 13286762496*x0^3*y0^2 - 8964490752*x0*y0^4 + 21420491904*x0^4 - 81064351872*x0^2*y0^2 + 16377709824*y0^4 - 79701302016*x0^3 + 225238583808*x0*y0^2 + 140773472784*x0^2 - 237434851584*y0^2 - 102883042080*x0 + 25767954576=0

在sqrt(6)域中分解得到：
-264*x0^2*y0*sqrt(6) + 88*y0^3*sqrt(6) + 5264*x0*y0*sqrt(6) + 956*x0^3 - 2868*x0*y0^2 - 15190*y0*sqrt(6) - 9884*x0^2 + 9884*y0^2 + 26705*x0 - 13377=0

264*x0^2*y0*sqrt(6) - 88*y0^3*sqrt(6) - 5264*x0*y0*sqrt(6) + 956*x0^3 - 2868*x0*y0^2 + 15190*y0*sqrt(6) - 9884*x0^2 + 9884*y0^2 + 26705*x0 - 13377=0

hujunhua

自迪卡尔1637年发明坐标几何之后，平面几何日薄西山，渐沉渐寂。
但精巧奇妙的几何定理仍然有着不可抗拒的魅力，不时闪耀出星芒。
比如莫莱三角形定理（1899），蝴蝶定理（1815~1944）。

本坛这个等边六边形定理应该也算一个，我仿佛看到了它隐隐的萤光。

各位还知道哪些这种精巧奇妙的几何定理？

wayne

题干 翻译成 alphageometry的表达， 输入到alphageometry求解器直接报错， 用ddar求解器没有报错， 但是 跑了两个小时。还没抛出结果。（说明求解器不认识）

1. a b c = triangle a b c; c d e = triangle c d e; e f a = triangle e f a;  a = eqdistance b b c;  b = eqdistance c c d; c = eqdistance d d e; e = eqdistance f f a; f = eqdistance a a b; h = midpoint h a c; j = midpoint j e c; l = midpoint l a e; k = midpoint k d f; g = midpoint g b f; i = midpoint i b d; m = on_line h k, on_line i l ? coll m g j
   

复制代码

感兴趣的可以一起玩玩， https://github.com/google-deepmind/alphageometry

换成以下描述作为输入，可以不停的刷屏，说明求解器成功解析了题目，并且正在搜索和迭代运行

1. b d f = triangle b d f; k = midpoint k d f; e = on_bline e d f; i = midpoint i b d; c = on_bline c b d, on_circle c d e; g = midpoint g b f; a = on_circle a b c, on_circle a f e; h = midpoint h a c; j = midpoint j e c; l = midpoint l a e; m = on_line m h k, on_line m i l ? coll m g j

复制代码

只可惜 最后的反馈是 无法求解。

1. I0404 16:09:37.007539 129033586689856 alphageometry.py:575] Solving: "a b c = triangle a b c; d = midpoint d b c; e = on_bline e b c; f = midpoint f a b; g = on_bline g a b, on_circle g b e; h = midpoint h a c; i = on_circle i a g, on_circle i c e; j = midpoint j i g; k = midpoint k e g; l = midpoint l i e; m = on_line m j d, on_line m f l; n = on_tline n a a c; o = on_pline o n a c ? coll m h k"
   
2. I0404 16:09:37.007640 129033586689856 graph.py:498]
   
3. I0404 16:09:37.007671 129033586689856 graph.py:499] a b c = triangle a b c; d = midpoint d b c; e = on_bline e b c; f = midpoint f a b; g = on_bline g a b, on_circle g b e; h = midpoint h a c; i = on_circle i a g, on_circle i c e; j = midpoint j i g; k = midpoint k e g; l = midpoint l i e; m = on_line m j d, on_line m f l; n = on_tline n a a c; o = on_pline o n a c ? coll m h k
   
4. I0404 16:09:38.404927 129033586689856 ddar.py:60] Depth 1/1000 time = 1.333711862564087
   
5. I0404 16:09:40.636892 129033586689856 ddar.py:60] Depth 2/1000 time = 2.2317442893981934
   
6. I0404 16:09:43.695074 129033586689856 ddar.py:60] Depth 3/1000 time = 3.058032989501953
   
7. I0404 16:09:50.548813 129033586689856 ddar.py:60] Depth 4/1000 time = 6.853524923324585
   
8. I0404 16:09:57.719603 129033586689856 ddar.py:60] Depth 5/1000 time = 7.170551300048828
   
9. I0404 16:10:04.945822 129033586689856 ddar.py:60] Depth 6/1000 time = 7.225924015045166
   
10. I0404 16:10:11.941211 129033586689856 ddar.py:60] Depth 7/1000 time = 6.994575500488281
    
11. I0404 16:10:19.254608 129033586689856 ddar.py:60] Depth 8/1000 time = 7.256026029586792
    
12. I0404 16:10:26.688832 129033586689856 ddar.py:60] Depth 9/1000 time = 7.434005975723267
    
13. I0404 16:10:34.647840 129033586689856 ddar.py:60] Depth 10/1000 time = 7.958703517913818
    
14. I0404 16:10:42.773855 129033586689856 ddar.py:60] Depth 11/1000 time = 8.125824689865112
    
15. I0404 16:10:50.538877 129033586689856 ddar.py:60] Depth 12/1000 time = 7.764830589294434
    
16. I0404 16:10:59.399841 129033586689856 ddar.py:60] Depth 13/1000 time = 8.83964991569519
    
17. I0404 16:10:59.404213 129033586689856 alphageometry.py:221] DD+AR failed to solve the problem.
    

复制代码

wayne

a = eqdistance b b c;是代表新定义一个点A,使得AB=BC. k = midpoint k d f代表是新建一个点K,K是DF的中点。这两句有效的前提是旧的点 在前面已经出现过。

----

我经过很多次尝试，发现这些语句是以分号作结尾，标点符号有讲究，比如空格用错了 会影响语法的解析， 每句话都代表着一个尺规作图的动作，所以要注意顺序，
不能基于未定义的点去定义新的点，也不能重复出现同一个点。如果要对同一个点多次描述，就需要合并起来，用逗号语句来描述。但并不是所有的操作都能合并，比如两个eqdistance定义一个点就不行。


关于更多的关键词定义，我搜遍了全网，没有可以参考的文档手册，最好的参考就是看代码，https://github.com/google-deepmi ... /blob/main/defs.txt
然后参考examples去理解关键词

wayne

alphageometry其实比较鸡贼。是先尝试用代数方法，DD+AR (if memory serves, it stands for "Deductive Database + Algebraic Relations")， DDAR解决不了，再尝试AI.

官方提供的案例是近20年的30道IMO题目，只有25道题目可以解决，而这25道题目，有14道题目是通过代数方法解决的，，真正是AI解决的只有11道， 所以说，别看 alphageometry发到了science,但其实可能 名不副实。


参考文章： https://www.reddit.com/r/math/co ... e_on_alphageometry/