等边六边形三线共点猜想

dlsh · 发表于 2024-4-28 21:37:14

mathe 发表于 2024-3-14 13:11
以下用大写字母表示位置矢量，黑体小写字母表示自由向量。

如图，设等边六边形`ABCDEF`的顶点`A`在原点 ...

如何区别内外六边形？这猜想对于内六边形可能也对。复数方法思路：
用AEC作基本图形，假设$e^{i\alpha}=u,e^{i\beta}=,e^{i\gamma}=w$,由向量定比分点公式可以求出D，E和F，再求出顺次各中点，由于是非线性构造，固定u,难点是如何根据等边条件求v,w?

hujunhua · 发表于 2024-4-29 00:53:16

使用复数方法，不一定要运用定比分点公式，或许使用复数形式的直线方程更适宜。
通过`z_1, z_2`的复数形式直线方程为 `(\bar z_2-\bar z_1)z-(z_2-z_1)\bar z=z_1\bar z_2-\bar z_1z_2`
三线共点的判据也是三条直线方程的复系数行列式等于0.
所以直线`GJ, KH, IL`共点的判据就是\[\begin{vmatrix}
J-G&\bar J-\bar G&G\bar J-\bar GJ\\
H-K&\bar H-\bar K&K\bar H-\bar KH\\
L-I&\bar L-\bar I&I\bar L-\bar IL\\
\end{vmatrix}=0\]将`G, H, I, J, K, L`代换成`\boldsymbol{a},\boldsymbol{b},\boldsymbol{c},\boldsymbol{d},\boldsymbol{e},\boldsymbol{f}`表达式，再验证上述行列式的值，计算量貌似比9#的向量方法大多了。

hejoseph · 发表于 2024-4-29 23:14:42

本帖最后由 hejoseph 于 2024-4-30 08:35 编辑

边数大于3的可不只是凸和凹那么简单，还有边自交的情形。例如四边形就有凸、凹、自交三种情形。六边形的情形就复杂太多了，例如下图的自交六边形。

还会存在互相平行的情形，这种可以看成交点在无穷远处。

数学星空 · 发表于 2024-4-30 08:57:38

接30#，设等边六边形$AC_1BA_1CB_1$边长为$x$, 两个间内接三角形ABC和$A_1B_1C_1$边长分别为$a,b,c,a_1,b_1,c_1$, 并且$AA_1=a_0,BB_1=b_0,CC_1=c_0$
再设等边六边形的6个顶角的半角依次为$α,β,γ,α_1,β_1,γ_1$

则有$α+β+γ+α_1+β_1+γ_1=2π$，并且：

$\sin α=\frac{a}{2x},\sin β=\frac{b}{2x},\sin γ=\frac{c}{2x}$

$\sin α_1=\frac{a_1}{2x},\sin β_1=\frac{b_1}{2x},\sin γ_1=\frac{c_1}{2x}$

以下皆以${α,β,γ},{α_1,β_1,γ_1},{a,b,c},{a_1,b_1,c_1}$各为遍历集，以〔〕表示遍历组合取和, 例如〔α〕:=α+β+γ。

设 $x\sin﹝α﹞=x\sin﹝-α_1﹞=T$ 展开得到：

$16T^4x^2-8a_1b_1c_1T^3 + 4(﹝a_1^2b_1^2﹞-2﹝a_1^2﹞x^2)T^2 -2a_1b_1c_1(﹝a_1^2﹞-8x^2)T + (﹝a_1^4﹞- 2﹝a_1^2b_1^2﹞)x^2 + a_1^2b_1^2c_1^2 =0$

$16T^4x^2+8abcT^3 + 4(﹝a^2b^2﹞-2﹝a^2﹞x^2)T^2 + 2abc(﹝a^2﹞-8x^2)T + (﹝a^4﹞ - 2﹝a^2b^2﹞)x^2 + a^2b^2c^2 =0$

将三角形的面积和外径量代换进去可以化为

$16T^4x^2-32T^3R_1s_1+4(﹝a_1^2b_1^2﹞-2﹝a_1^2﹞x^2)T^2-8R_1s_1(﹝a_1^2b_1^2﹞-32R_1s_1x^2)T-16s_1^2(x^2-R_1^2)=0$

$16T^4x^2+32T^3Rs+4(﹝a^2b^2﹞-2﹝a^2﹞x^2)T^2+8Rs(﹝a^2b^2﹞-32Rsx^2)T-16s^2(x^2-R^2)=0$

若$﹝α﹞=﹝α_1﹞=\pi$, 则有 $T=x\sin(\pi)=0$ 代入得到

$16s_1^2(x^2-R_1^2)=0$

$16s^2(x^2-R^2)=0$

即$R_1=R=x$

dlsh · 发表于 2024-4-30 22:54:46

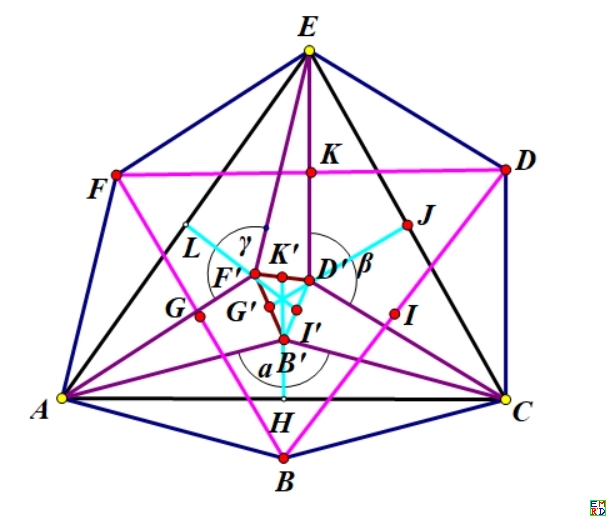
\!$\*OverscriptBox[\(a$, $_$]\) = 1/a;
\!$\*OverscriptBox[\(e$, $_$]\) = 1/e;
\!$\*OverscriptBox[\(c$, $_$]\) = 1/c;
\!$\*OverscriptBox[\(u$, $_$]\) = 1/u;
\!$\*OverscriptBox[\(v$, $_$]\) = 1/v;
\!$\*OverscriptBox[\(w$, $_$]\) = 1/w;(*三角形AEC外接圆心作原点
e^i\[Gamma]=u,e^i\[Beta]=w,e^i\[Beta]=v*)
Fendian[t_, a_, b_] := (a - t b )/(1 - t );
\!$\*OverscriptBox[\(Fendian$, $_$]\)[t_, a_, b_] := (
\!$\*OverscriptBox[\(a$, $_$]\) -
\!$\*OverscriptBox[\(t$, $_$]\)
\!$\*OverscriptBox[\(\(b$$\ $\), $_$]\))/(1 -
\!$\*OverscriptBox[\(\(t$$\ $\), $_$]\) );
Md[a_, b_] := (a + b )/2;
\!$\*OverscriptBox[\(Md$, $_$]\)[a_, b_] := (
\!$\*OverscriptBox[\(a$, $_$]\) +
\!$\*OverscriptBox[\(\(b$$\ $\), $_$]\))/2 ;
f = (a u - e)/(u - 1);
\!$\*OverscriptBox[\(f$, $_$]\) = (
\!$\*OverscriptBox[\(\(a$$\ $\), $_$]\)/u -
\!$\*OverscriptBox[\(e$, $_$]\))/(
\!$\*OverscriptBox[\(u$, $_$]\) - 1); d = (e v - c)/(v - 1);
\!$\*OverscriptBox[\(d$, $_$]\) = (
\!$\*OverscriptBox[\(e$, $_$]\)/v -
\!$\*OverscriptBox[\(c$, $_$]\))/(
\!$\*OverscriptBox[\(v$, $_$]\) - 1); b = (c w - a)/(w - 1);
\!$\*OverscriptBox[\(b$, $_$]\) = (
\!$\*OverscriptBox[\(c$, $_$]\)/w -
\!$\*OverscriptBox[\(a$, $_$]\))/(
\!$\*OverscriptBox[\(w$, $_$]\) - 1);
L = Md[a, e];
\!$\*OverscriptBox[\(L$, $_$]\) =
\!$\*OverscriptBox[\(Md$, $_$]\)[a, e]; g = Md[f, b];
\!$\*OverscriptBox[\(g$, $_$]\) =
\!$\*OverscriptBox[\(Md$, $_$]\)[f, b];
h = Md[a, c];
\!$\*OverscriptBox[\(h$, $_$]\) =
\!$\*OverscriptBox[\(Md$, $_$]\)[a, c]; i = Md[d, b];
\!$\*OverscriptBox[\(i$, $_$]\) =
\!$\*OverscriptBox[\(Md$, $_$]\)[d, b];
j = Md[c, e];
\!$\*OverscriptBox[\(j$, $_$]\) =
\!$\*OverscriptBox[\(Md$, $_$]\)[c, e]; k = Md[d, f];
\!$\*OverscriptBox[\(k$, $_$]\) =
\!$\*OverscriptBox[\(Md$, $_$]\)[d, f];
Sqd[a_, b_] := (a - b) (
\!$\*OverscriptBox[\(a$, $_$]\) -
\!$\*OverscriptBox[\(b$, $_$]\));(*AB距离平方*)
Juli[a_, b_] := Sqrt[Sqd[a, b]];(*AB距离*)
KAB[a_, b_] := (a - b)/(
\!$\*OverscriptBox[\(a$, $_$]\) -
\!$\*OverscriptBox[\(b$, $_$]\));(*复斜率定义*)
(*Overscript[KAB, _][a_,b_]:=1/KAB[a,b];*)
Angle2[a_, b_, c_] := KAB[a, b]/KAB[b, c];(*e^(2iB)等于复斜率相除*)
\!$\*OverscriptBox[\(Jd$, $_$]\)[k1_, a1_, k2_, a2_] := -((a1 - k1
\!$\*OverscriptBox[\(a1$, $_$]\) - (a2 - k2
\!$\*OverscriptBox[\(a2$, $_$]\)))/(
k1 - k2));(*复斜率等于k1,过点A1与复斜率等于k2,过点A2的直线交点*)
Jd[k1_, a1_, k2_, a2_] := -((k2 (a1 - k1
\!$\*OverscriptBox[\(a1$, $_$]\)) - k1 (a2 - k2
\!$\*OverscriptBox[\(a2$, $_$]\)))/(k1 - k2));
FourPoint[a_, b_, c_, d_] := ((
\!$\*OverscriptBox[\(c$, $_$]\) d - c
\!$\*OverscriptBox[\(d$, $_$]\)) (a - b) - (
\!$\*OverscriptBox[\(a$, $_$]\) b - a
\!$\*OverscriptBox[\(b$, $_$]\)) (c - d))/((a - b) (
\!$\*OverscriptBox[\(c$, $_$]\) -
\!$\*OverscriptBox[\(d$, $_$]\)) - (
\!$\*OverscriptBox[\(a$, $_$]\) -
\!$\*OverscriptBox[\(b$, $_$]\)) (c - d));(*过两点A和B、C和D的交点*)
\!$\*OverscriptBox[\(FourPoint$, $_$]\)[a_, b_, c_, d_] := -(((c
\!$\*OverscriptBox[\(d$, $_$]\) -
\!$\*OverscriptBox[\(c$, $_$]\) d) (
\!$\*OverscriptBox[\(a$, $_$]\) -
\!$\*OverscriptBox[\(b$, $_$]\)) - ( a
\!$\*OverscriptBox[\(b$, $_$]\) -
\!$\*OverscriptBox[\(a$, $_$]\) b) (
\!$\*OverscriptBox[\(c$, $_$]\) -
\!$\*OverscriptBox[\(d$, $_$]\)))/((a - b) (
\!$\*OverscriptBox[\(c$, $_$]\) -
\!$\*OverscriptBox[\(d$, $_$]\)) - (
\!$\*OverscriptBox[\(a$, $_$]\) -
\!$\*OverscriptBox[\(b$, $_$]\)) (c - d)));
n1 = FourPoint[k, h, L, i]; n2 = FourPoint[k, h, g, j];
Simplify[{1, Sqd[e, f], Sqd[e, d], Sqd[a, b]}]
Simplify[{2, Sqd[e, f] - Sqd[e, d], , Sqd[e, f] - Sqd[a, b]}]
FullSimplify[{21, Sqd[e, f] - Sqd[e, d], , Sqd[e, f] - Sqd[a, b]}]
Factor[{20, Sqd[e, f] - Sqd[e, d], , Sqd[e, f] - Sqd[a, b]}]
Simplify[{3, n1, n2, , n1 - n2}]
Factor[{30, n1, n2, , n1 - n2}]

复制代码

复数方法对于非线性构造没有优势

数学星空 · 发表于 2024-5-1 23:21:55

根据30#结果，我们可以得到
当$x=R=R_1$时
$a_0=\sqrt{\frac{b^2+c^2-a^2}{2}+x^2-2s_0\sqrt{4(\frac{x}{a})^2-1}}$
   $=\sqrt{bc\cos(A)+R^2-2\frac{abc}{4R}\frac{\sqrt{4R^2-a^2}}{a}}$
   $=\sqrt{bc\cos(A)+R^2-\frac{bc}{2R}2R\cos(A)}$
   $=R$
同理可得到$b_0=c_0=R$
$a_1=\sqrt{\frac{b_0^2+x^2-c^2}{2}+x^2+2s_1\sqrt{4(\frac{x}{c})^2-1}}$
      $=\sqrt{\frac{R^2+R^2-c^2}{2}+R^2+2\frac{c}{2}\sqrt{R^2-(\frac{c}{2})^2}\sqrt{4(\frac{R}{c})^2-1}}$
      $=\sqrt{2R^2-\frac{c^2}{2}+2(R^2-(\frac{c}{2})^2)}$
      $=\sqrt{4R^2-c^2}$
同理可得到
$b_1=\sqrt{4R^2-a^2}$
$c_1=\sqrt{4R^2-b^2}$
即有$a_1^2+c^2=b_1^2+a^2=c_1^2+b^2=4R^2$
又由$R_1=\frac{a_1b_1c_1}{\sqrt{2a_1^2b_1^2+2a_1^2c_1^2+2b_1^2c_1^2-a_1^4-b_1^4-c_1^4}}$
代入上面关系化简得到
$(4R^3-(a^2+b^2+c^2)R+abc)(4R^3-(a^2+b^2+c^2)R-abc)=0$
进一步代入
$R=\frac{abc}{\sqrt{2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4}}$
展开化简得到
$(a^4+b^4+c^4-2a^2(b^2+c^2))(a^4+b^4+c^4-2b^2(a^2+c^2))(a^4+b^4+c^4-2c^2(b^2+a^2))=0$

例：取$a=3,b=4$代入上面各个关系可以得到6组解
$[a = 3, b = 4, c = 1.269844648, R = 2.828427127, a_1 = 5.512485340, b_1 = 4.795831529, c_1 = 4.000000006, R_1 = 2.828427130]$
$[a = 3, b = 4, c = 1.828427125, R = 2.121320344, a_1 = 3.828427126, b_1 = 3.000000002, c_1 = 1.414213566, R_1 = 2.121320344]$
$[a = 3, b = 4, c = 2.833626166, R = 2.003676277, a_1 = 2.833626165, b_1 = 2.656854247, c_1 = 0.2426406602, R_1 = 2.003676543]$
$[a = 3, b = 4, c = 5.512485335, R = 2.828427125, a_1 = 1.269844648, b_1 = 4.795831523, c_1 = 4.000000000, R_1 = 2.828427125]$
$[a = 3, b = 4, c = 3.828427125, R = 2.121320343, a_1 = 1.828427122, b_1 = 2.999999998, c_1 = 1.414213559, R_1 = 2.121320354]$
$[a = 3, b = 4, c = 6.478469167, R = 4.580969476, a_1 = 6.478469156, b_1 = 8.656854242, c_1 = 8.242640679, R_1 = 4.580969474]$

creasson · 发表于 2024-5-2 19:44:31

由1#的图，不妨设$A=0,  B=1$,  又令\[
a = {e^{i\angle A}},b = {e^{i\angle B}},c = {e^{i\angle C}},f = {e^{i\angle F}}
\]则可由\[
\frac{{F - A}}{{B - A}} = a,\frac{{E - F}}{{A - F}} = f,\frac{{C - B}}{{A - B}} = \frac{1}{b},\frac{{D - C}}{{B - C}} = \frac{1}{c}
\]得到各点的一个表示\[A = 0, B = 1, C = 1 - \frac{1}{b},D = \frac{{1 - c + bc}}{{bc}}, E = a - af, F = a
\]约束条件由$DE=1$给出\[
1 - c + bc - abc - f + af - abf + cf - acf - bcf + 4abcf - {a^2}bcf - a{b^2}cf + {a^2}{b^2}cf - ab{c^2}f + a{b^2}{c^2}f - {a^2}{b^2}{c^2}f - abc{f^2} + {a^2}bc{f^2} - {a^2}{b^2}c{f^2} + {a^2}{b^2}{c^2}{f^2} = 0
\]有点遗憾的是, 不能得到有理参数化解.

若要保证是凸六边形，要求\[
\Im a > 0, \Im b > 0, \Im c > 0, \Im f > 0, \Im \frac{{1 - c + bc - abc + abcf}}{{abcf}} > 0, \Im \frac{1}{{1 - c + bc - abc + abcf}} > 0\]
交点$M$的表示为\[
M = \frac{{ - b - ab + f + abf - cf + bcf}}{{2b( - 1 + cf)}}
\]两个三角形的外接圆半径平方表示则是\[
R_1^2 = \frac{{b( - 1 + a - ab + abc)( - 1 + c - bc + abc)}}{{{{( - 1 + a{b^2}c)}^2}}}\\
R_2^2 = \frac{{a( - 1 + b - ab + abf)( - 1 + f - af + abf)}}{{{{( - 1 + {a^2}bf)}^2}}}
\]与边长1相减而有\[
1 - R_1^2 = \frac{{(1 - b)(1 + ab)(1 + bc)(1 - abc)}}{{{{(1 - a{b^2}c)}^2}}}\\
1 - R_2^2 = \frac{{(1 - a)(1 + ab)(1 + af)(1 - abf)}}{{{{(1 - {a^2}bf)}^2}}}
\]如果$R_1 = R_2 = 1$, 则$c = f = \frac{1}{ab} $, 各点的表示则是\[
A = 0,B = 1,C = 1 - \frac{1}{b},D = 1 + a - \frac{1}{b},{\rm E} = a - \frac{1}{b}, F = a
\]可令\[
a = \frac{{1 + is}}{{1 - is}},b = \frac{{1 + it}}{{1 - it}},c = \frac{{1 + iu}}{{1 - iu}},f = \frac{{1 + iv}}{{1 - iv}}
\]转化到实数域上讨论, 凸等边六边形的约束条件即为:
\[{-s - s t^2 - u + s^2 u + 4 s t u + t^2 u - s^2 t^2 u + s u^2 + 2 t u^2 - 2 s^2 t u^2 - 3 s t^2 u^2 + 2 s^2 v + 2 s^2 t^2 v + 4 s u v + 4 t u v - 4 s^2 t u v - 4 s t^2 u v + 2 u^2 v - 8 s t u^2 v - 2 t^2 u^2 v + 4 s^2 t^2 u^2 v + s v^2 + s t^2 v^2 +u v^2 - s^2 u v^2 - 4 s t u v^2 - t^2 u v^2 + s^2 t^2 u v^2 -s u^2 v^2 - 2 t u^2 v^2 + 2 s^2 t u^2 v^2 + 3 s t^2 u^2 v^2 >  0, \\
-t - s^2 t + 2 t^2 u + 2 s^2 t^2 u + t u^2 + s^2 t u^2 - v + s^2 v + 4 s t v + t^2 v - s^2 t^2 v + 4 s u v + 4 t u v - 4 s^2 t u v - 4 s t^2 u v + u^2 v - s^2 u^2 v - 4 s t u^2 v - t^2 u^2 v + s^2 t^2 u^2 v + 2 s v^2 + t v^2 - 3 s^2 t v^2 - 2 s t^2 v^2 + 2 u v^2 - 2 s^2 u v^2 - 8 s t u v^2 + 4 s^2 t^2 u v^2 - 2 s u^2 v^2 - t u^2 v^2 + 3 s^2 t u^2 v^2 + 2 s t^2 u^2 v^2 >  0,\\
-t u - s^2 t u + t^2 u^2 + s^2 t^2 u^2 - s v - s t^2 v - u v +s^2 u v + 4 s t u v + t^2 u v - s^2 t^2 u v + s u^2 v +2 t u^2 v - 2 s^2 t u^2 v - 3 s t^2 u^2 v + s^2 v^2 +s^2 t^2 v^2 + 2 s u v^2 + t u v^2 - 3 s^2 t u v^2 - 2 s t^2 u v^2 +u^2 v^2 - 4 s t u^2 v^2 + 3 s^2 t^2 u^2 v^2 == 0, s > 0, t > 0, u > 0, v > 0}
\]若$R_1, R_2$ 同时大于1, 又要求\[
(-1 + s t) (-1 + t u) (-s - t - u + s t u) > 0, \\
(-1 + s t) (-1 + s v) (-s - t - v + s t v) > 0
\]mathematica 表明这是不可能的.

mathe · 发表于 5 天前

我把这个题目发到知乎上，网友卡布奇诺指出了存在一种非常不错的几何证明方法
如下图，取对角线CF中点N,AD中点O,连接KO,HO,KN,HN。于是KO和HN都平行等于FA/2, KN和HO都平行等于CD/2, FA=CD,所以KOHN是菱形。KH垂直平分NO。
也就是说，M是六边形ABCDEF三条主对角线中点N,O,P构成三角形的外心。

hujunhua · 发表于 5 天前

mathe 发表于 2024-5-9 10:59
我把这个题目发到知乎上，网友卡布奇诺指出了存在一种非常不错的几何证明方法
如下图，取对角线CF中点N,AD ...

三圆足矣，三个等圆好奢侈。但是，冗枝不自坠，开花亦结果。

原来三个等圆的根心，正是三个圆心构成的三角形的外心。非等圆不可如是外心证根心。

dlsh · 发表于前天 21:17

设O是△ACE的外心，o作各边对称点获得其它各点，则这种简化情形中，胡心P是三角形ACE的九点圆心。

账号		自动登录	找回密码
密码			欢迎注册

[猜想] 等边六边形三线共点猜想

点评

点评

评分

点评

点评

点评