等边六边形三线共点猜想

xiaoshuchong

补充一个观察，等边六边形的另外三条边几乎相交在一点。

实际上并不相交，只是离得很近，以下是放大50倍的图

数学星空

36#楼因为根号前的正负号弄反了，现在重新更正如下：

根据30#结果，我们可以得到
当\(x=R=R_1\)时
\(a_0=\sqrt{\frac{b^2+c^2-a^2}{2}+x^2+2s_0\sqrt{4(\frac{x}{a})^2-1}}\)
      \(=\sqrt{bc\cos(A)+R^2+2\frac{abc}{4R}\frac{\sqrt{4R^2-a^2}}{a}}\)
       \(=\sqrt{bc\cos(A)+R^2+\frac{bc}{2R}2R\cos(A)}\)
       \(=\sqrt{2bc\cos(A)+R^2}\)
       \(=\sqrt{b^2+c^2-a^2+R^2}\)
同理可得到
\(b_0=\sqrt{a^2+c^2-b^2+R^2}\)
\(c_0=\sqrt{a^2+b^2-c^2+R^2}\)

进一步可以计算
\(16s_1^2=<b,c_0,x>=2b^2c_0^2+2b^2x^2+2c_0^2x^2-b^4-c_0^4-x^4\)
           \(=<b,\sqrt{2bc\cos(A)+R^2},R>=4b^2R^2+2ac\cos(B)(b^2-2ac\cos(B))\)

\(s_1=\frac{b^2(a^2+c^2)-(a^2-c^2)^2}{4abc}R\)

\(\sqrt{4(\frac{x}{b})^2-1}=\sqrt{4(\frac{R}{b})^2-1}\)
                                   \(=\sqrt{4(\frac{R}{2R\sin(B)})^2-1}\)
                                   \(=\frac{\cos(B)}{\sin(B)}\)
                                   \(=\frac{a^2-b^2+c^2}{abc}R\)

又由30#结论有

\(a_1=\sqrt{\frac{c_0^2+x^2-b^2}{2}+x^2+2s_1\sqrt{4(\frac{x}{b})^2-1}}\)

则可以得到：

\(a_1^2=\frac{c_0^2+x^2-b^2}{2}+x^2+2s_1\sqrt{4(\frac{x}{b})^2-1}\)
          \(=\frac{a^2+b^2-c^2+R^2+R^2-b^2}{2}+R^2+2s_1\sqrt{4(\frac{x}{b})^2-1}\)
          \(=\frac{a^2-c^2}{2}+2R^2+2\frac{b^2(a^2+c^2)-(a^2-c^2)^2}{4abc}R\frac{a^2-b^2+c^2}{abc}R\)
          \(=\frac{a^2-c^2}{2}+2R^2+2R^2\frac{b^2(a^2+c^2)-(a^2-c^2)^2}{4a^2b^2c^2}(a^2-b^2+c^2)\)
          \(=\frac{a^2-c^2}{2}+2R^2+2R^2\frac{4a^2c^2-(a^2+c^2)(a^2+c^2-b^2)}{4a^2b^2c^2}(a^2-b^2+c^2)\)
          \(=\frac{a^2-c^2}{2}+2R^2+2R^2\frac{4a^2c^2-(a^2+c^2)(2ac\cos(B))}{4a^2b^2c^2}(2ac\cos(B))\)
         \(=\frac{a^2-c^2}{2}+2R^2+2R^2\frac{2ac\cos(B)-(a^2+c^2)\cos(B)^2}{b^2}\)
         \(=\frac{a^2-c^2}{2}+2R^2+2R^2\frac{a^2+c^2-b^2-(a^2+c^2)(1-\sin(B)^2)}{b^2}\)
         \(=\frac{a^2-c^2}{2}+2R^2+2R^2\frac{-b^2+(a^2+c^2)\sin(B)^2}{b^2}\)
         \(=\frac{a^2-c^2}{2}+2R^2+2R^2(\frac{a^2+c^2}{4R^2}-1)\)
         \(=\frac{a^2-c^2}{2}+\frac{a^2+c^2}{2}\)
         \(=a^2\)
同理可得到
\(b_1=b\)
\(c_1=c\)
这样可以得到，两个内接三角形全等，对应顶角相等

两个内接三角形外心的间距\(d\) 可以继续研究哈~~

0.1110

把“等边六边形”弱化为“对边相等的六边形”，我猜三线共点的结论也成立

hujunhua

还真是成立㖿！

而且38#的那个外心证法仍然有效，倒是14#的三圆证法失效了。
由于3#所述仿射变换的缘故，六边相等并不是必要条件，所以上述弱化（的约束）虽然令人惊艳，却也不是十分意外。
但是，不得不承认，这使得等边六边形定理的光芒暗淡了一些。并且显得“六边相等”的描述有点偷懒。
按仿射变换，对边相等也不是必要条件，或许还能转换出一个别的约束。

0.1110

数学星空

现在我们来计算有关两个内接三角形的外心间距\(d\)

对于三角形\(ABC\)内两点\(P,Q\),若三角形三边长分别为\(a,b,c\),\(PA=x,PB=y,PC=z,QA=x1,QB=y1,QC=z1,PQ=d\),则有下列关系式：

-a^4*d^4 + 2*a^4*d^2*x^2 + 2*a^4*d^2*x1^2 - a^4*x^4 + 2*a^4*x^2*x1^2 - a^4*x1^4 + 4*a^2*b^2*c^2*d^2 + 2*a^2*b^2*d^4 - 2*a^2*b^2*d^2*x^2 - 2*a^2*b^2*d^2*x1^2 - 2*a^2*b^2*d^2*y^2 - 2*a^2*b^2*d^2*y1^2 + 2*a^2*b^2*x^2*y^2 - 2*a^2*b^2*x^2*y1^2 - 2*a^2*b^2*x1^2*y^2 + 2*a^2*b^2*x1^2*y1^2 + 2*a^2*c^2*d^4 - 2*a^2*c^2*d^2*x^2 - 2*a^2*c^2*d^2*x1^2 - 2*a^2*c^2*d^2*z^2 - 2*a^2*c^2*d^2*z1^2 + 2*a^2*c^2*x^2*z^2 - 2*a^2*c^2*x^2*z1^2 - 2*a^2*c^2*x1^2*z^2 + 2*a^2*c^2*x1^2*z1^2 + 4*a^2*d^2*x^2*x1^2 - 2*a^2*d^2*x^2*y1^2 - 2*a^2*d^2*x^2*z1^2 - 2*a^2*d^2*x1^2*y^2 - 2*a^2*d^2*x1^2*z^2 + 2*a^2*d^2*y^2*z1^2 + 2*a^2*d^2*y1^2*z^2 + 2*a^2*x^4*y1^2 + 2*a^2*x^4*z1^2 - 2*a^2*x^2*x1^2*y^2 - 2*a^2*x^2*x1^2*y1^2 - 2*a^2*x^2*x1^2*z^2 - 2*a^2*x^2*x1^2*z1^2 - 2*a^2*x^2*y^2*z1^2 - 2*a^2*x^2*y1^2*z^2 + 4*a^2*x^2*y1^2*z1^2 + 2*a^2*x1^4*y^2 + 2*a^2*x1^4*z^2 + 4*a^2*x1^2*y^2*z^2 - 2*a^2*x1^2*y^2*z1^2 - 2*a^2*x1^2*y1^2*z^2 - b^4*d^4 + 2*b^4*d^2*y^2 + 2*b^4*d^2*y1^2 - b^4*y^4 + 2*b^4*y^2*y1^2 - b^4*y1^4 + 2*b^2*c^2*d^4 - 2*b^2*c^2*d^2*y^2 - 2*b^2*c^2*d^2*y1^2 - 2*b^2*c^2*d^2*z^2 - 2*b^2*c^2*d^2*z1^2 + 2*b^2*c^2*y^2*z^2 - 2*b^2*c^2*y^2*z1^2 - 2*b^2*c^2*y1^2*z^2 + 2*b^2*c^2*y1^2*z1^2 - 2*b^2*d^2*x^2*y1^2 + 2*b^2*d^2*x^2*z1^2 - 2*b^2*d^2*x1^2*y^2 + 2*b^2*d^2*x1^2*z^2 + 4*b^2*d^2*y^2*y1^2 - 2*b^2*d^2*y^2*z1^2 - 2*b^2*d^2*y1^2*z^2 - 2*b^2*x^2*y^2*y1^2 - 2*b^2*x^2*y^2*z1^2 + 2*b^2*x^2*y1^4 + 4*b^2*x^2*y1^2*z^2 - 2*b^2*x^2*y1^2*z1^2 + 2*b^2*x1^2*y^4 - 2*b^2*x1^2*y^2*y1^2 - 2*b^2*x1^2*y^2*z^2 + 4*b^2*x1^2*y^2*z1^2 - 2*b^2*x1^2*y1^2*z^2 + 2*b^2*y^4*z1^2 - 2*b^2*y^2*y1^2*z^2 - 2*b^2*y^2*y1^2*z1^2 + 2*b^2*y1^4*z^2 - c^4*d^4 + 2*c^4*d^2*z^2 + 2*c^4*d^2*z1^2 - c^4*z^4 + 2*c^4*z^2*z1^2 - c^4*z1^4 + 2*c^2*d^2*x^2*y1^2 - 2*c^2*d^2*x^2*z1^2 + 2*c^2*d^2*x1^2*y^2 - 2*c^2*d^2*x1^2*z^2 - 2*c^2*d^2*y^2*z1^2 - 2*c^2*d^2*y1^2*z^2 + 4*c^2*d^2*z^2*z1^2 + 4*c^2*x^2*y^2*z1^2 - 2*c^2*x^2*y1^2*z^2 - 2*c^2*x^2*y1^2*z1^2 - 2*c^2*x^2*z^2*z1^2 + 2*c^2*x^2*z1^4 - 2*c^2*x1^2*y^2*z^2 - 2*c^2*x1^2*y^2*z1^2 + 4*c^2*x1^2*y1^2*z^2 + 2*c^2*x1^2*z^4 - 2*c^2*x1^2*z^2*z1^2 - 2*c^2*y^2*z^2*z1^2 + 2*c^2*y^2*z1^4 + 2*c^2*y1^2*z^4 - 2*c^2*y1^2*z^2*z1^2 - x^4*y1^4 + 2*x^4*y1^2*z1^2 - x^4*z1^4 + 2*x^2*x1^2*y^2*y1^2 - 2*x^2*x1^2*y^2*z1^2 - 2*x^2*x1^2*y1^2*z^2 + 2*x^2*x1^2*z^2*z1^2 - 2*x^2*y^2*y1^2*z1^2 + 2*x^2*y^2*z1^4 + 2*x^2*y1^4*z^2 - 2*x^2*y1^2*z^2*z1^2 - x1^4*y^4 + 2*x1^4*y^2*z^2 - x1^4*z^4 + 2*x1^2*y^4*z1^2 - 2*x1^2*y^2*y1^2*z^2 - 2*x1^2*y^2*z^2*z1^2 + 2*x1^2*y1^2*z^4 - y^4*z1^4 + 2*y^2*y1^2*z^2*z1^2 - y1^4*z^4=0

对于两个内接三角形的外心及楼上的相关计算结果有：

\(x=R,y=R,z=R\)

代入化简得到：

\(a^4d^2 - a^4x_1^2 - a^2b^2c^2 - 2a^2b^2d^2 + a^2b^2x_1^2 + a^2b^2y_1^2 - 2a^2c^2d^2 + a^2c^2x_1^2 + a^2c^2z_1^2 + b^4d^2 - b^4y_1^2 - 2b^2c^2d^2 + b^2c^2y_1^2 + b^2c^2z_1^2 + c^4d^2 - c^4z_1^2=0\)

且

\(x_1=\sqrt{x_0^2-(\frac{a_1}{2})^2}+\sqrt{R_1^2-(\frac{a_1}{2})^2}\)

\(y_1=\sqrt{x_0^2-(\frac{b_1}{2})^2}+\sqrt{R_1^2-(\frac{b_1}{2})^2}\)

\(z_1=\sqrt{x_0^2-(\frac{c_1}{2})^2}+\sqrt{R_1^2-(\frac{c_1}{2})^2}\)

转化为代数方程有：

\(R_1^4 - 2R_1^2x_0^2 - 2R_1^2x_1^2 + a_1^2x_1^2 + x_0^4 - 2x_0^2x_1^2 + x_1^4=0\)

\(R_1^4 - 2R_1^2x_0^2 - 2R_1^2y_1^2 + b_1^2y_1^2 + x_0^4 - 2x_0^2y_1^2 + y_1^4=0\)

\(R_1^4 - 2R_1^2x_0^2 - 2R_1^2z_1^2 + c_1^2z_1^2 + x_0^4 - 2x_0^2z_1^2 + z_1^4=0\)

特别的，若\(x=R=R_1\) 则有

\(a_1=a,b_1=b,c_1=c\)

代入上面三个代数方程有：

\(x_1=\sqrt{4R^2-a^2},y_1=\sqrt{4R^2-b^2},z_1=\sqrt{4R^2-c^2}\)

进一步代入关于\(d\)的代数方程中化简得到：

\(a^6 - a^4b^2 - a^4c^2 - a^2b^4 + 3a^2b^2c^2 - a^2c^4 + b^6 - b^4c^2 - b^2c^4 + c^6 + d^2(a + b + c)(a - b - c)(a - b + c)(a + b - c)=0\)


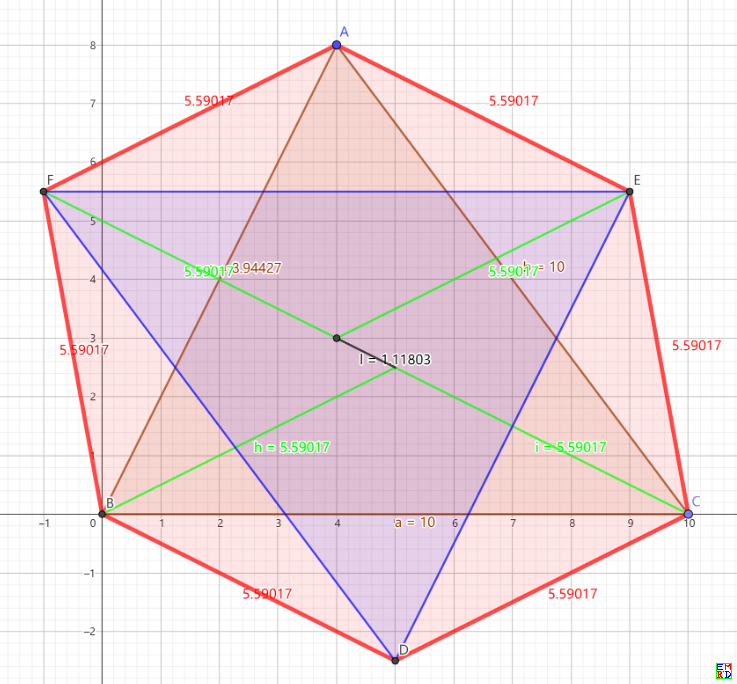
例如(下面数值解）

\(R = 5.59017, R_1 = 5.59017, a = 10,  a_1 = 10, b = 10,  b_1 = 10, c = 8.94427,  c_1 = 8.94427, d = 1.11803, x_0 = 5.59017\)