果树问题最优解大全

mathe

我也不知道m4是什么玩意。也许你可以下载一个旧一点版本的gmp. 不过如果仅仅使用gmp,你可以去下载一个事先编译好的windows下的gmp库，我找到过一个4.2.1版本的，如果你有csdn帐号，可以直接下载: http://download.csdn.net/source/318770

wayne

刚才我又编译了一遍。 仔细看了make install的信息：

3. wayne@waytop:~/gmp-4.3.1$ make install
4. make install-recursive
5. make[1]: Entering directory `/home/wayne/gmp-4.3.1'
6. Making install in tests
7. make[2]: Entering directory `/home/wayne/gmp-4.3.1/tests'
8. Making install in .
9. 。。。。。。。。。。。。
10. test -z "/usr/local/info" || mkdir -p -- . "/usr/local/info"
11. mkdir: cannot create directory `/usr/local/info': Permission denied
12. make[3]: *** [install-info-am] Error 1
13. make[3]: Leaving directory `/home/wayne/gmp-4.3.1/doc'
14. make[2]: *** [install-am] Error 2
15. make[2]: Leaving directory `/home/wayne/gmp-4.3.1/doc'
16. make[1]: *** [install-recursive] Error 1
17. make[1]: Leaving directory `/home/wayne/gmp-4.3.1'
18. make: *** [install] Error 2
19. wayne@waytop:~/gmp-4.3.1$

复制代码

原来，仅在configure和make花的时间较长，在敲make install时又自动变成了普通用户，导致 mkdir: cannot create directory `/usr/local/info': Permission denied

mathe

你要转化为root用户然后才能够运行make install

mathe

现在弄了个gp代码，它可以将一个给定图的所有可能的对称轴（经过投影变换以后）都找出来了。 用这个处理20棵树23行的那个有理解，我作出一个对称的等价解（程序标明只有一个对称轴），不过还没有完全消除无穷远点: 同样我们可以通过投影变换将次对称轴投影到无穷远直线，从而得到一个中心对称的图形: 程序find_node_trans_all()可以返回所有的可能的对称轴，结果是一个矩阵，每一行代表一个对称轴， 其中每一行六个数，其中前3个数是所有同对称点连线的交点（或者我们可以称为对称轴的极点）的齐次坐标，后面3个数是对称轴的齐次坐标。 只是程序运行挺慢的 ocdgp.zip (7.77 KB, 下载次数: 5)

2009-12-25 14:33 上传

点击文件名下载附件

wayne

,我只在configure那一步加了sudo，后面的都没加，原来问题出在这

mathe

呵呵，我通常是直接 su root

wayne

哦，这个命令在ubuntu下默认是用不了的. 安装貌似没有异常，可你的程序还是调用不了gmp,算了，放弃了 看来gmp一般人还是用不了的 好像是安Ctrl+Alt+1可以切换到字符终端，应该能够以root登录的。当然你需要先设置root的密码。 这个通过passwd root可以设置。 现在是编译不了，链接不成功，还是运行不了？ 实在不行可以通过g++ -I{gmp.h的路径} -L{libgmp.a的路径} 来指定路径，如果是动态链接，还需要运行时设置环境LD_LIBRARY_PATH（不过好像gmp默认是静态链接的）。 我觉得你可以试用一下windows下预编译的版本。当然在工程中同样需要设置头文件路径和库文件路径

wayne

我可以在mathematica里面多加一点额外的处理，不是大问题的。 现在该把重点放在理解你的坐标表达式

mathe

处理完了，。。。 总共有12情况有实数解 具体情况见附件 wayne 发表于 2009-12-24 10:18

16#的附件中方程和点线关系不匹配。应该是脚本有问题

mathe

我现在对18棵树18行的一个数据非常感兴趣，因为它每棵树也正好是4行。 点线关系为: AEHIABGKCEGLCDKMBDFNBCHOEFJOADLOBJLPAFMPCINPDGIQHJMQEKNQFGHRIJKRLMNROPQR solve([+1-1*P_Y*Q_X-2*P_Y*Q_Y+2*Q_Y*Q_Y+1*R_Y-1*P_Y*R_Y+1*Q_Y*R_Y,+1*J_X-1*P_Y*Q_X-2*P_Y*Q_Y+2*Q_Y*Q_Y+1*J_X*R_Y,+1*J_Y-1*J_X*Q_Y+1*R_Y-1*J_X*R_Y-1*P_Y*R_Y+1*Q_Y*R_Y,+1*N_X-2*P_Y*Q_X-3*P_Y*Q_Y+3*Q_Y*Q_Y+2*R_Y+1*N_X*R_Y-2*P_Y*R_Y+2*Q_Y*R_Y,+1*N_Y-1*N_X*Q_Y-1*N_X*R_Y,+1*O_X-1*O_X*Q_Y+1*R_Y-1*P_Y*R_Y+1*Q_Y*R_Y,+1*J_Y*O_X-1*P_Y*Q_X-2*P_Y*Q_Y+2*Q_Y*Q_Y+1*J_X*R_Y,+1*P_X-1*P_X*R_Y+1*Q_X*R_Y,+1*P_Y-1*P_Y*Q_X-1*P_Y*Q_Y+1*Q_Y*Q_Y,+1*J_X*P_Y-1*J_X*Q_Y+1*R_Y-1*J_X*R_Y-1*P_Y*R_Y+1*Q_Y*R_Y,+1*J_Y*P_Y-1*P_Y*Q_X+1*J_X*Q_Y-1*J_Y*Q_Y-1*P_Y*Q_Y+1*Q_Y*Q_Y-1*R_Y+1*J_X*R_Y+1*P_Y*R_Y-1*Q_Y*R_Y,+1*N_X*P_Y+1*N_Y*P_Y-2*P_Y*Q_X-1*N_X*Q_Y-1*N_Y*Q_Y-2*P_Y*Q_Y+2*Q_Y*Q_Y+2*R_Y-2*P_Y*R_Y+2*Q_Y*R_Y,+1*O_X*P_Y-1*O_X*Q_Y+1*R_Y-1*P_Y*R_Y-1*Q_X*R_Y+1*Q_Y*R_Y,+1*Q_X-1*P_Y*Q_X-1*P_Y*Q_Y+1*Q_Y*Q_Y+1*Q_X*R_Y,+1*N_Y*Q_X+1*P_Y*Q_X-1*N_X*Q_Y+2*P_Y*Q_Y-2*Q_Y*Q_Y-1*R_Y-1*N_X*R_Y+1*P_Y*R_Y-1*Q_Y*R_Y,+1*Q_Y-1*R_Y+1*P_Y*R_Y-1*Q_Y*R_Y,+1*P_X*Q_Y+1*P_Y*Q_Y-1*Q_Y*Q_Y-1*R_Y-1*P_X*R_Y+1*P_Y*R_Y+1*Q_X*R_Y-1*Q_Y*R_Y,+1*Q_X*Q_Y-1*R_Y+1*P_Y*R_Y+1*Q_X*R_Y-1*Q_Y*R_Y,-1+1*M_X+1*P_Y-1*Q_Y,+1*K_Y-1*Q_Y-1*R_Y,-1+1*C_Y+1*Q_Y,+1*I_X-1*Q_X,-1+1*F_X,-1+1*R_X,+1+1*B_Y-1*Q_Y,-1+1*O_Y,+1*F_Y-1*P_Y,+1*M_Y-1*P_Y,+1*D_X-1*Q_X,-1+1*D_Y],[J_X,J_Y,N_X,N_Y,O_X,P_X,P_Y,Q_X,Q_Y,R_Y,M_X,K_Y,C_Y,I_X,F_X,R_X,B_Y,O_Y,F_Y,M_Y,D_X,D_Y]); print("A=(1,0,0) B=(1,B_y,0) C_x=0 E_x=0 E_y=0 G=(0,1,0) H_x=1 H_y=0 I_y=0 K=(1,K_y,0) L_x=0 L_y=1 "); 原始图像为: 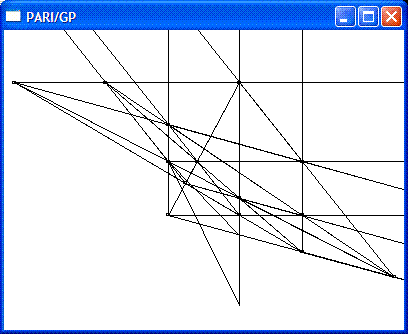经过gp分析只有一条对称轴，将对称轴映射到无穷远直线，变成中心对称的图为4个点在无穷远） 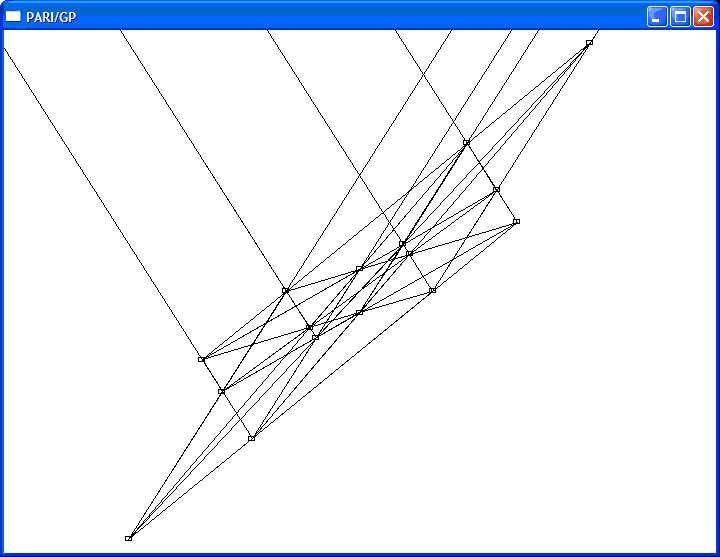将对称轴映射到x轴为: 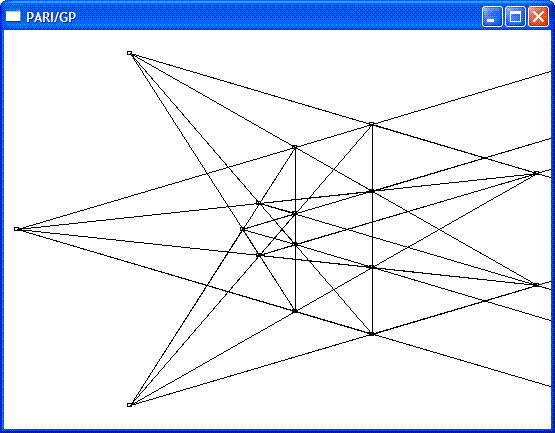再次消除无穷远点得到:
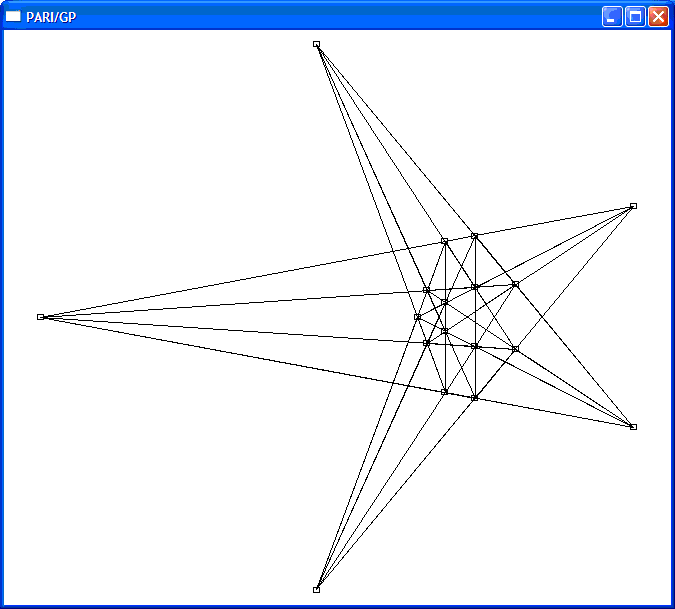