果树问题最优解大全

wayne

16#楼的文件我更新了，前面的都是些罗嗦的代码。
你可以直接看最后的结果：
数字表示对应的方程在s18.len18.out文件的行数

mathe

我的那个ocd.gp程序里面有很多代码，你可以参考一下看看。当然代码有点难读懂，而且使用起来自动化程度还太低，最后变换矩阵还都是要手工输入，还需要继续加强。不过现在那个18棵树18行的图转化的还是挺成功的

mathe

同样，7#中19棵树20行的情况也只有一条对称轴，
首先是中心对称图：

其次是几个不同的左右对称图:



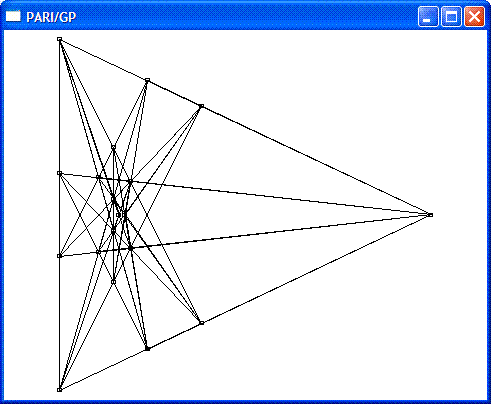
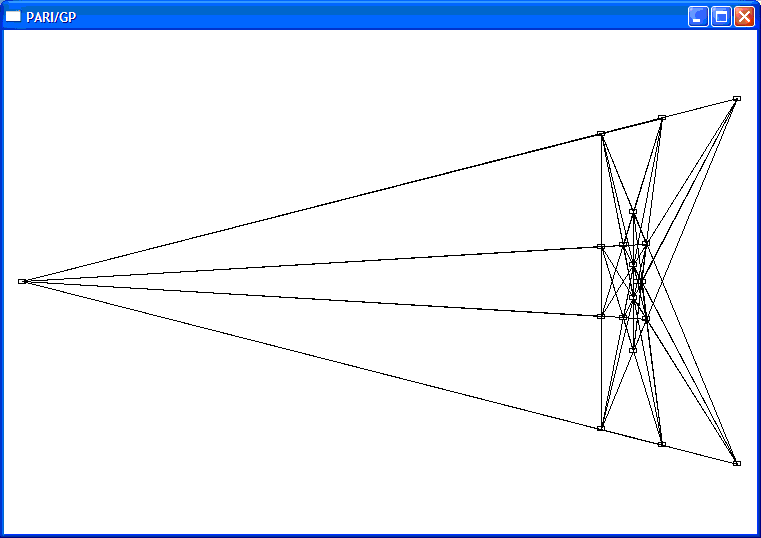
(以上3个实际上都只在x轴进行了投影变换)
比如最后一个坐标如下(实际计算中将所有的模去掉，同时t用sqrt(5)替换）:
[Mod(1/3, t^2 - 5) Mod(1/6*t + 1/6, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(1/2, t^2 - 5) Mod(-1/4*t + 1/4, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(1/22*t + 7/22, t^2 - 5) Mod(5/22*t - 9/22, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(1/2, t^2 - 5) Mod(1/4*t - 1/4, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(1/22*t + 7/22, t^2 - 5) Mod(-5/22*t + 9/22, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(1/3, t^2 - 5) Mod(-1/6*t - 1/6, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(-1/2*t + 3/2, t^2 - 5) Mod(5*t - 11, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(1/22*t + 7/22, t^2 - 5) Mod(1/22*t + 7/22, t^2 - 5) Mod(1, t^2 - 5)]
[0 Mod(1, t^2 - 5) Mod(1, t^2 - 5)]
[0 Mod(-1, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(3/38*t + 11/38, t^2 - 5) 0 Mod(1, t^2 - 5)]
[Mod(1/3, t^2 - 5) Mod(1/6*t - 1/2, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(-1/22*t + 7/22, t^2 - 5) 0 Mod(1, t^2 - 5)]
[Mod(1/10*t + 1/2, t^2 - 5) Mod(3/5*t + 1, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(1/3, t^2 - 5) Mod(-1/6*t + 1/2, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(1/22*t + 7/22, t^2 - 5) Mod(-1/22*t - 7/22, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(1/10*t + 1/2, t^2 - 5) Mod(-3/5*t - 1, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(-1/2*t + 3/2, t^2 - 5) Mod(-5*t + 11, t^2 - 5) Mod(1, t^2 - 5)]
[Mod(1/62*t + 25/62, t^2 - 5) 0 Mod(1, t^2 - 5)]

mathe

用那个ocd.gp产生上面的图需要使用下面的方法:
i)首先修改文件中前6个函数,用这个方法来输入数据。
ii)在gp中使用
\r ocd
来装入这个文件内容（文件保存在c盘根目录就可以）
iii)输入命令:
    nnodes=get_node_num();
    nedges=get_edge_num();
    edge_matrix=get_edge_matrix(nedges,get_edge_string());
    oldnc=get_nodes_info();
    node_coord=Mod(oldnc, get_mod_poly());
iv)输入命令
verify_input(nnodes,nedges,edge_matrix,node_coord)
如果返回结果是0，那么说明输入数据有错误，应该是手误。
v)输入命令
verify_inputs()
如果没有报告任何信息，说明数据合法，不然应该存在5点共线，是增根。
vi)输入命令
a=find_node_trans_all()
来获取所有对称轴信息。
现在我遇到情况都只有一条对称轴，那么第一个测试可以将对称轴投影到无穷远
m=matrix(1,3);
m[1,]=[a[1,1],a[1,2],a[1,3]];
r=matker(m)~;
r=concat(r,[a[1,4],a[1,5],a[1,6]]);
nc=normalize_coord(node_coord*r~);
show_algebra(edge_matrix,nc)
这里，将显示中心对称的图
然后使用命令
u=r;
r[3,]=u[2,];
r[2,]=u[3,];
然后对变量x进行赋值给任意一个常数
r[3,]=r[3,]+x*r[1,];
nc=normalize_coord(node_coord*r~);
show_algebra(edge_matrix,nc)
将显示一个左右对称的图。

wayne

nc=normalize_coord(nood_coord*r~);这行命令是不是敲错了，运行的时候提示：

array index (4) out of allowed range [1-3].

wayne

好像因为是get_nodes_info函数没有返回值

mathe

nc=normalize_coord(nood_coord*r~);
你改成
nc=normalize_coord(nood_coord*(r~));
试一试，难道~（求转置的优先级更低??)

wayne

问题应该不在这，因为get_nodes_info()不返回结果，所以
oldnc为空，于是 命令nc=normalize_coord(nood_coord*r~)就无效了

mathe

拼写错误
nood_coord
＝》
node_coord

wayne

呵呵，直接敲变量名，Gp竟然echo为一堆的空行~~~

%%%%%%%%%%%%%%%%%%%%%

倒数第二行命令没改过来，看样子不是你敲错了，而是曾经用过这种名字，。
但即便是改过来了，最后一个命令还是没通过