果树问题讨论:这两个问题等价么？

sheng_jianguo

关于20棵树植树问题研究的一些想法（一) 1.定义与历史回顾 20棵树植树问题是果园问题(最初由Sylvester在1867年提出)中最引人关注美妙问题。 为了便于分析讨论，先给出问题中的一些名称的定义。 广义果园问题：平面上n个点，若其中任m+1个点不共线，问恰过其中m个点的直线最多有几条？（n＞m） 当n=20，m=4时，就是20棵树植树问题，其中满足条件的最多直线条数记为maxt4。（可以证明maxt4≤26） 20棵树的i行图（简称i行图）：由平面上20个点（其中任5个点不共线）和所有恰过其中4个点的i条直线组成的图。 大家知道，在二十世纪七十年代，两位数学爱好者巧妙地运用电子计算机成功地绘制出了精湛美丽（由三个五角星构成）的20行图，后来据说国外有人曾以二十万美金设奖希望对此能有新的突破。 参见http://202.38.126.65/navigate/mathcolumn/artical1.htm

mathe

这个链接信息有点旧了。论坛里面有标签功能，选择里面的标签“果树问题”可以看到一些相关信息。现在已经有两个23行图被找到了。

sheng_jianguo

关于20棵树植树问题研究的一些想法（二) 2.近期进展 大家可能不知道，在1985年，我国的伍毛成功地绘制出了21行植树图（当初查资料时，在《自学》1985年3期中看到记下的，现在网上查到的大多是我近年来回答网友时给出的图，原图画的不严格，修整后见下图，称为21行W图）。 　　　　　　　　21行W图 近年来，已有多人给出了23行图，查到的有以下几位： 2005年，Lin Xianzu（我想应是中国人）证明了至少存在23行的植树法，并给出了在射影平面上的23行图（有2个点在无穷远处，https://oeis.org/A006065/a006065.gif 图中少画了一根直线，修整后见下图，称为23行L图）。 　　　　　　　　　　　23行L图 注：注：在21行W图中，如果将E和O点移到无穷远处，增加DS和CT两条直线，并将K点移到增加的两线交点处，就成了23行L图。 2006年，辽宁锦州开发区笔架山小学王兴君成功地绘制出了欧氏平面中23行图（http://www.eol.cn/zheng_ming_1877/20060309/t20060309_166193.shtml，图画的不太严格，修整后见下图，称为23行W图）。 　　　　　　　　　　　23行W图 2009年，河北省邢台学院学生黄阳阳（昵称eyond）成功地绘制出了另一个漂亮的23行植树图（/thread-1418-1-1.html，图形稍作调整后见下图，称为23行H图 ）。 　　　　　　　　　　23行H图 最近，我们这里的领军人Du Zhaohui（昵称mathe）计算搜索出了射影平面上的另一个不太对称的23行植树图（有4个点和1条直线在无穷远处，/viewthread.php?tid=1261&page=3&fromuid=20#pid17137，图形稍作调整后见下图，称为23行D图 ）。 　　　　　　　　　　　　23行D图 关于以上4个23行图之间是否是本质上相同的（射影等价），将在下一节讨论。 对于20棵树植树问题，我当初的猜想是：maxt4≤24，但maxt4=24的可能性很小。 最近大家在这里的大量计算工作，目的是想验证maxt4≥24是否成立，现在得出的结论是： maxt4=24成立的可能性几乎不存在。

sheng_jianguo

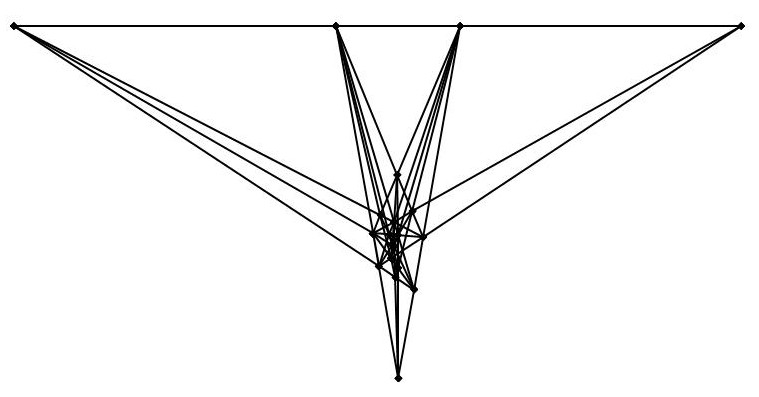关于20棵树植树问题研究的一些想法（三) 3.射影变换 为了直观起见，我们总希望将射影平面上有无穷远点的图形通过线性变换（一一对应）到欧氏平面中图，而通过射影几何中的简单(中心)射影变换就很容易做到这一点（虽然当初在大学数学系数学专业里没学过射影几何，但看了一些资料后觉得实际上并不难做到）： 直观讲，假定P和E是两个射影平面，O是两平面外的一点（射影中心），(中心)射影变换就是将P平面上任一点A对应到E平面上一点B，使OA和OB在一条直线上。（一般的射影变换就是有经过限次中心射影变换的变换） 对于P中任意n 个点的图，我们适当调整两平面夹角及O点位置，就可以射影变换成E中n 个不是无穷远点的图。 根据上面想法，我前几天编了这样的实用软件。下面看看前面提到的射影平面中23行L图和23行D图通过此软件变换到欧氏平面中是怎样的： 　　　　　　　　　欧氏平面中23行L图 　　　　　　　　　欧氏平面中23行D图 　　　　　　　　　欧氏平面中23行D图（局部） 注：zgg__在http://bbs.emath.ac.cn/viewthread.php?tid=1303&page=1&fromuid=20#pid17254中给出的23行图不是射影到欧氏平面中的23行D图，而旋转90度后不难看出就是23行H图。 这个通用计算绘图软件（Excel文件）压缩后在下面给出，有兴趣可试一试（只要将其中蓝颜色数据修改成需要变换图形的坐标（可以直接输入，也可输入公式计算）和直线标号就可因计算绘图了，绿颜色数据用于调整图形，可以不改，黑颜色数据自动计算，不用修改）。 射影变换.rar (16.89 KB, 下载次数: 4)

2009-12-17 10:40 上传

点击文件名下载附件

下面简单说明，已找到的4个23行图之间任2个图都不是射影等价的（即不存在射影变换使一个图形对应成另一个图形）。 为此，先定义点线图T的点线关系集Tdx={|n为恰经过m条线的点的个数} 如23行D图的点线关系集为{<6,3>,<5,7>,<4,9>,<3,1>}(表明此图恰经过6条线的点有3个，恰经过5条线的点有7个，恰经过4条线的点有9个，恰经过3条线的点有1个) 23行L图的点线关系集为{<5,14>,<4,4>,<3,2>} 23行W图的点线关系集为{<6,4>,<5,5>,<4,10>,<3,1>} 23行H图的点线关系集为{<6,4>,<5,5>,<4,10>,<3,1>} 由于射影变换后点线关系集不变，故只有23行W图和23行H图可能射影等价，但点线图的子集射影变换后点线关系集也不变，而23行W图有一个5个点的子图（其中1个三角形的3个顶点都恰经过6条线）的点线关系集为{<6,3>,<4,1>,<3,1>}，23行H图任何一个5个点这样的子图的点线关系集都不是{<6,3>,<4,1>,<3,1>}，所以23行W图和23行H图也不是射影等价的。 由于存在23行D图，我估计23行图不止以上4种。 但无论如何，如果一个找所有24行图的程序是正确的，那么将它方法修改成找23行图的程序时，它一定能找到以上4种23行图。

数学星空

嗯,总结的非常好,希望我们"数学研发网"的团队,能再接再励,在mathe的领导下,给出关于20颗树问题迄今最为完整的答案,我想mathe和sheng_jianguo可以组织编写关于这个问题更详细的资料及其最终结果 这也许是我们团队第一次合作的成果,也是2009年献给数学爱好者最完美的礼物

sheng_jianguo

关于20棵树植树问题研究的一些想法（四) 4.需要做的工作 要完美解决20棵树植树问题，需要完成以下工作： 严格证明maxt4=X（X是23、24、25、26中一数），如果X=23，并将所有23行图分类，搞清23行图共有几种（任2种图之间都不是射影等价的）。 我们目前可以做的是： 用编程法严格验证maxt4≥24是否成立。如果验证maxt4≥24不成立（可能性很大），为了把工作做得更完美及考证程序正确性，建议开展如下工作： 1.如果计算量不大，用同样方法去寻找23行图，和22行图（目前我还没有看到有22行图公布），找22行图的原因是从22行图可能直接发现是否有24行图（就像前面提到的21行W图很容易扩展成23行L图）。 2.请mathe在这里详细介绍用编程法验证maxt4≥24的思路过程，使大家明白在做什么，为什么这样做。 （如我不明白原始计算fidxx文件中数据（16点图）为什么是完备的即没有漏掉其它数据（16点图）？整数集、分数集是可数无穷集，实数集、复数集的势更大是不可数无穷集，而计算机只能判断有限个数，为什么能保证不会漏掉要求解的数据？） 5.结论 在20棵树植树问题研究中有一个现象值得关注，那就是此问题的进展大多都是由（中国）业余数学爱好者完成而非专业数学专家完成，这说明此问题适合一般大众进行研究。 相信用不了多久，这个非常有意思的世界数学难题一定会在我们中国人的努力下得到完美解决。

mathe

我分析出来是王兴君,eyond,和我给出的那三个结果是等价的。可以分析它们的点线关系会发现它们是一致的。而对于对应的点线关系，解方程我只找到一个解。

mathe

关于20棵树植树问题研究的一些想法（四) 4.需要做的工作 要完美解决20棵树植树问题，需要完成以下工作： 严格证明maxt4=X（X是23、24、25、26中一数），如果X=23，并将所有23行图分类，搞清23行图共有几种（任2种 ... sheng_jianguo 发表于 2009-12-17 10:45

现在用我们的程序应该可以找出所有19棵树20行的结果。然后由此我们可以得出所有20棵树其中某一颗树只有不超过3行的所有23行结果。（但是可能还有20棵树23行的结果每棵树都4行以上的存在，不过可能性不是太大）

mathe

现在在2#添加了一些算法介绍

winxos

nid10, nid11全部计算完成， 结果为空。 winxos 2009-12-18