果树问题讨论:这两个问题等价么？

mathe · 发表于 2020-1-6 11:43:41

16棵15行实数解（两个应该都具有很强的对称性）有
      Parameter [+1+3*t+1*t^2=0](Real)
      A[+1+1*t ,-1*t , +1]
      B[0 ,+1 , 0]
      C[+1 ,0 , 0]
      D[-1*t ,+1+1*t , +1]
      E[0 ,0 , +1]
      F[+1 ,+1 , +1]
      G[0 ,+1 , +1]
      H[+1 ,+2+1*t , 0]
      I[+1 ,+1+1*t , 0]
      J[+1 ,0 , +1]
      K[0 ,-1*t , +1]
      L[-1*t ,0 , +1]
      M[+1+1*t ,+1 , +1]
      N[+1 ,+1+1*t , +1]
      O[-1*t ,-1*t , +1]
      P[+1+1*t ,+1+1*t , +1]
BCHIADGJBEGKDFIKAFHLCEJLCFGMDEHMAEINBFJNACKOBDLOABMPCDNPEFOP
（这个试验出了五边形嵌套图）

      Parameter [-1+1*t+1*t^2=0](Real)
      A[+1 ,0 , +1]
      B[0 ,+1 , 0]
      C[0 ,0 , +1]
      D[-1-1*t ,+1 , +1]
      E[+1 ,-1 , 0]
      F[-1*t ,+1 , +1]
      G[0 ,+1 , +1]
      H[-1*t ,+1*t , +1]
      I[+1 ,0 , 0]
      J[-1-1*t ,+1+1*t , +1]
      K[+1 ,-1*t , 0]
      L[0 ,+1-1*t , +1]
      M[-1-1*t ,0 , +1]
      N[+1 ,-1*t , +1]
      O[-1*t ,+1+1*t , +1]
      P[+1 ,+1+1*t , +1]
DFGICEHJBEIKAFJKBCGLADHLACIMBDJMCDKNEFLNAEGOBFHOGHMPABNPIJOP

但是16棵14行整数解都无法对称，比如
      A[+1 ,0 , 0](Integer)
      B[+1 ,-2 , 0]
      C[+1 ,0 , +1]
      D[0 ,+1 , 0]
      E[0 ,+1 , +1]
      F[0 ,0 , +1]
      G[+1 ,-1 , +1]
      H[+1 ,-1 , 0]
      I[0 ,+2 , +1]
      J[+1/2 ,0 , +1]
      K[+1/2 ,+1 , +1]
      L[-1 ,+2 , +1]
      M[+1/2 ,-1 , +1]
      N[+1 ,+1 , +1]
      O[-2 ,+2 , +1]
      P[+3 ,-1 , +1]
ABDHDEFIACFJBEGJBCIKCEHLDJKMBFLMCDGNAEKNFGHOAILOAGMPHINP

      A[+1 ,0 , 0]
      B[0 ,+1 , 0]
      C[+1 ,0 , +1]
      D[+1 ,-1/2 , 0]
      E[0 ,0 , +1]
      F[0 ,+1 , +1]
      G[+2 ,-1 , +1]
      H[-1 ,+1 , +1]
      I[+1 ,-1 , 0]
      J[0 ,+1/2 , +1]
      K[+1 ,+1/2 , +1]
      L[+2 ,0 , +1]
      M[+1 ,-1 , +1]
      N[-1 ,+1/2 , +1]
      O[+2 ,+1 , +1]
      P[-1 ,-1 , +1]
ABDICFGIBEFJCDHJACELDFKLEHIMBCKMDEGNAJKNAFHOBGLOAGMPBHNP

mathe · 发表于 2020-1-6 12:11:24

17棵15行整数解很多，但是基本上不对称，对称的有:

      A[+1 ,0 , 0]
      B[0 ,+1 , 0]
      C[+1 ,0 , +1]
      D[+1 ,+1 , 0]
      E[+1 ,+1 , +1]
      F[0 ,+1 , +1]
      G[+1 ,-1 , 0]
      H[0 ,0 , +1]
      I[+1/2 ,+1/2 , +1]
      J[+1/2 ,+3/2 , +1]
      K[0 ,-1 , +1]
      L[+1 ,-1 , +1]
      M[+3/2 ,+1/2 , +1]
      N[-1 ,0 , +1]
      O[-1 ,+1 , +1]
      P[+1/2 ,-1 , +1]
      Q[-1 ,+1/2 , +1]
ABDGCFGIDEHIBFHKBCELEGJMCDKMACHNDFJNAEFOGHLOBIJPAKLPAIMQBNOQ
(AB) (CF) (D) (E) (G) (H) (I) (JM) (KN) (LO) (PQ), DEHI是对称轴

      A[+1 ,0 , 0]
      B[0 ,+1 , 0]
      C[0 ,0 , +1]
      D[0 ,+1 , +1]
      E[+1 ,-1 , 0]
      F[+1 ,+1 , +1]
      G[+1 ,+1 , 0]
      H[0 ,-1 , +1]
      I[+1 ,0 , +1]
      J[+1 ,-1 , +1]
      K[-2 ,0 , +1]
      L[-2 ,-1 , +1]
      M[-2 ,+1 , +1]
      N[-1/2 ,+1/2 , +1]
      O[-1/2 ,-1/2 , +1]
      P[+1/4 ,+3/4 , +1]
      Q[+1/4 ,-3/4 , +1]
ABEGBCDHBFIJACIKAHJLADFMBKLMCEJNDGLNCFGOEHMODEIPFKNPGHIQJKOQ
(A) (B) (C) (DH) (EG) (FJ) (I）(K) (LM)  (NO) (PQ)， ACIK是对称轴

      A[+1 ,0 , 0]
      B[0 ,0 , +1]
      C[0 ,+1 , 0]
      D[+1 ,-2 , 0]
      E[0 ,+1 , +1]
      F[+1 ,+2 , 0]
      G[+1 ,0 , +1]
      H[+1/2 ,-1 , +1]
      I[0 ,-1 , +1]
      J[+1/2 ,+1 , +1]
      K[+1/4 ,0 , +1]
      L[+1 ,-1 , +1]
      M[+1 ,+1 , +1]
      N[+1/4 ,+1/2 , +1]
      O[+1/4 ,-1/2 , +1]
      P[-1/2 ,+3 , +1]
      Q[-1/2 ,-3 , +1]
ACDFBCEIABGKAHILAEJMCGLMBFJNDELNBDHOFIMOCKNODGJPEHKPFGHQIJKQ
(AB)  (C)  (DEFI) (GK) (HJ) (LMNO) (PQ)

      A[0 ,+1 , 0]
      B[0 ,+1 , +1]
      C[+1 ,0 , +1]
      D[0 ,0 , +1]
      E[+1 ,-1 , 0]
      F[+1 ,0 , 0]
      G[+1 ,+2 , +1]
      H[+1 ,+1 , 0]
      I[-1 ,+1 , +1]
      J[0 ,+2 , +1]
      K[-1 ,0 , +1]
      L[+1 ,+1 , +1]
      M[-1 ,-2 , +1]
      N[+1/3 ,+2/3 , +1]
      O[+3/2 ,+1/2 , +1]
      P[-2 ,+2 , +1]
      Q[-3 ,-1 , +1]
AEFHABDJCDFKBGHKACGLBFILAIKMBCENDGMNEJLOCHMODEIPFGJPHIJQKLNQ
(AB) (CK) (D) (EI) (F) (G) (HL) (J) (MN) (OQ) (P), FGJP是对称轴

...

mathe · 发表于 2020-1-6 13:09:08

18棵17行整数解，对称的有:
      A[0 ,+1 , +1]
      B[+1 ,0 , 0]
      C[+1 ,+1/2 , 0]
      D[+1 ,0 , +1]
      E[+1 ,+1 , 0]
      F[0 ,+1/2 , +1]
      G[0 ,0 , +1]
      H[+1 ,+2 , +1]
      I[0 ,+1 , 0]
      J[+2 ,+2 , +1]
      K[-1 ,0 , +1]
      L[+1/2 ,+1/2 , +1]
      M[+1 ,+3/2 , +1]
      N[+1/3 ,+2/3 , +1]
      O[+2 ,+1/2 , +1]
      P[+5 ,+2 , +1]
      Q[+1/2 ,+1 , +1]
      R[+2 ,+1 , +1]
BCEIAFGIBDGKAEHKEGJLDHIMACJMCFKNADLNBFLOBHJPCDOPEFMQGHNQIJORKLPRABQR
(A) (B) (CD) (EG) (FH) (IK) (JL) (MN) (OP) (Q) (R)， ABQR是对称轴

      A[-1 ,+1 , +1]
      B[0 ,+1 , 0]
      C[+1 ,0 , 0]
      D[0 ,+1 , +1]
      E[-2 ,+2 , +1]
      F[+1 ,+2 , +1]
      G[-1/2 ,+3/2 , +1]
      H[+1 ,0 , +1]
      I[+1 ,-1/2 , 0]
      J[0 ,+3/2 , +1]
      K[-1/2 ,+5/4 , +1]
      L[-1/2 ,+1/2 , +1]
      M[-2 ,+3/2 , +1]
      N[+1 ,+1 , 0]
      O[0 ,0 , +1]
      P[-2 ,0 , +1]
      Q[+1 ,+1 , +1]
      R[-1 ,+2 , +1]
DEIKAFJKBGKLAHIMCGJMBCINDFLNBDJOAELOBEMPAGNPCHOPACDQBFHQCEFRDGHRIJQR
(A) (B) (CD) (EG) (FH) (IJ) (KM) (LP) (NO) (Q) (R) ？

mathe · 发表于 2020-1-6 13:17:35

19棵20行整数解:

      A[+1 ,-1 , 0]
      B[+1 ,+1/2 , +1]
      C[+1 ,0 , 0]
      D[+1 ,-1/4 , 0]
      E[0 ,+1 , +1]
      F[0 ,+1 , 0]
      G[0 ,+1/2 , +1]
      H[-1 ,+1 , +1]
      I[+1 ,0 , +1]
      J[+2 ,0 , +1]
      K[0 ,0 , +1]
      L[-1 ,+3/2 , +1]
      M[+1 ,+1 , +1]
      N[-1 ,+1/2 , +1]
      O[-2/3 ,+2/3 , +1]
      P[+1/3 ,+1/6 , +1]
      Q[+1/3 ,+2/3 , +1]
      R[+4/3 ,+2/3 , +1]
      S[+1/3 ,+7/6 , +1]
ACDFEFGKCIJKBEJLCEHMBFIMBCGNFHLNDGJOAHKOAGLPDINPBDHQAEIQAJMRBKPRCOQRDLMSENOSFPQS
(AD) (BE) (CF) (G) (HI) (JL) (KN) (M)  (OP) (Q) (RS)

mathe · 发表于 2020-1-6 17:01:48

比如上面19棵20行，我们可以选择将AD, BE投影成正方形，结果得到
s19.1.png

可以发现点Q被投影成无穷远点。
但是注意到三个独立点Q,M,G在一条直线上，我们可以选择另外一条平行x轴的直线投影为无穷远可以继续保持对称性，
所以选择变换阵
$S=\begin{pmatrix} 1&0&0\\0&1&0\\0&1&-t\end{pmatrix}$
分别选择不同的参数t,可以得出如下的图:
s19.2.png

wayne · 发表于 2020-1-6 18:27:47

ACDFEFGKCIJKBEJLCEHMBFIMBCGNFHLNDGJOAHKOAGLPDINPBDHQAEIQAJMRBKPRCOQRDLMSENOSFPQS 的射影坐标是:

{{A,{1,-2,0}},{B,{1/2,1/2,1}},{C,{1,0,0}},{D,{1,-(1/2),0}},{E,{0,1,1}},{F,{0,1,0}},{G,{0,1/2,1}},{H,{-(1/2),1,1}},{I,{1/2,0,1}},{J,{1,0,1}},{K,{0,0,1}},{L,{-(1/2),3/2,1}},{M,{1/2,1,1}},{N,{-(1/2),1/2,1}},{O,{-(1/3),2/3,1}},{P,{1/6,1/6,1}},{Q,{1/6,2/3,1}},{R,{2/3,2/3,1}},{S,{1/6,7/6,1}}}

复制代码

数学星空 · 发表于 2020-1-6 18:54:19

19棵20行：

初始数据

[[A, C, D, F], [E, F, G, K], [C, I, J, K], [B, E, J, L], [C, E, H, M], [B, F, I, M], [B, C, G, N], [F, H, L, N], [D, G, J, O], [A, H, K, O], [A, G, L, P], [D, I, N, P], [B, D, H, Q], [A, E, I, Q], [A, J, M, R], [B, K, P, R], [C, O, Q, R], [D, L, M, S], [E, N, O, S], [F, P, Q, S]]

[[A, 1, -1, 0], [B, 1, 1/2, 1], [C, 1, 0, 0], [D, 1, -1/4, 0], [E, 0, 1, 1], [F, 0, 1, 0], [G, 0, 1/2, 1], [H, -1, 1, 1], [I, 1, 0, 1], [J, 2, 0, 1], [K, 0, 0, 1], [L, -1, 3/2, 1], [M, 1, 1, 1], [N, -1, 1/2, 1], [O, -2/3, 2/3, 1], [P, 1/3, 1/6, 1], [Q, 1/3, 2/3, 1], [R, 4/3, 2/3, 1], [S, 1/3, 7/6, 1]]

第一种：变换基点

M[1, 1, 1]-->[0, sqrt(3)/3, 1]
D[1, -1/4, 0]--> [-1/2, -sqrt(3)/6, 1]
A[1, -1, 0]--> [1/2, -sqrt(3)/6, 1]
Q[1/3, 2/3, 1]--> [0, 0, 1]

变换矩阵
[[-1/12, 1/6, -1/12], [-1/12*sqrt(3), -1/6*sqrt(3), 5/36*sqrt(3)], [1/2, 1, -11/6]]

变换后坐标

[1/2, -sqrt(3)/6, A], [1/10, sqrt(3)/30, B], [-1/6, -sqrt(3)/6, C], [-1/2, -sqrt(3)/6, D], [-1/10, sqrt(3)/30, E], [1/6, -sqrt(3)/6, F], [0, -sqrt(3)/24, G], [-1/8, -sqrt(3)/24, H], [1/8, -sqrt(3)/24, I], [3/10, sqrt(3)/30, J], [1/22, -(5*sqrt(3))/66, K], [-3/10, sqrt(3)/30, L], [0, sqrt(3)/3, M], [-1/22, -(5*sqrt(3))/66, N], [-1/18, -sqrt(3)/18, O], [1/18, -sqrt(3)/18, P], [0, 0, Q], [1/6, sqrt(3)/6, R], [-1/6, sqrt(3)/6, S]

画图得到

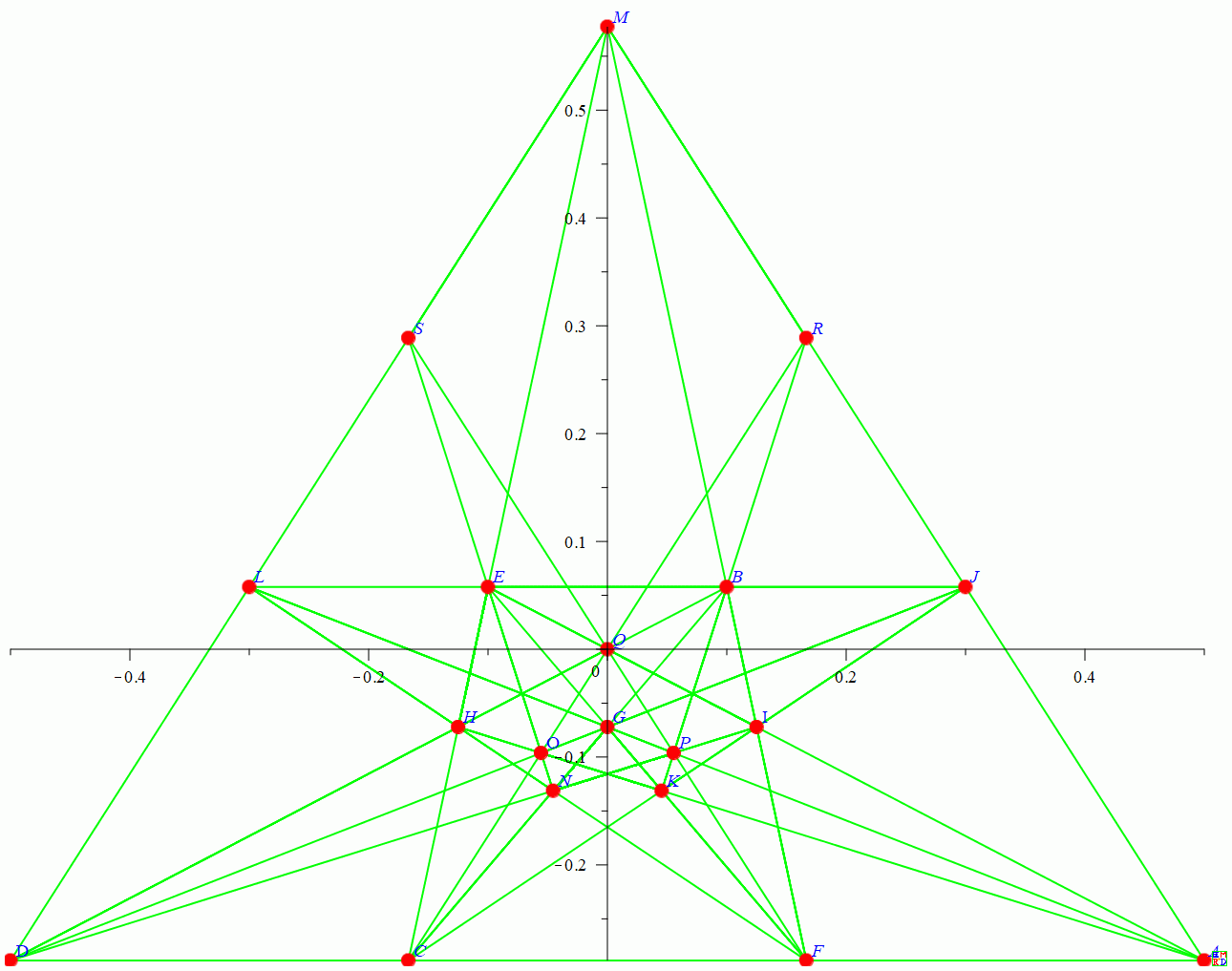
第二种：

变换基点：

O[-2/3, 2/3, 1]-->[-1, 1, 1]
K[0, 0, 1]--> [-1, -1, 1]
N[-1, 1/2, 1]--> [1, -1, 1]
P[1/3, 1/6, 1]--> [1, 1, 1]

变换矩阵

[[-1, 2, -1], [0, 0, -1], [-3, -6, 1]]

变换后坐标

[-1, 0, A], [1/5, 1/5, B], [1/3, 0, C], [1, 0, D], [-1/5, 1/5, E], [-1/3, 0, F], [0, 1/2, G], [-1, 1/2, H], [1, 1/2, I], [3/5, 1/5, J], [-1, -1, K], [-3/5, 1/5, L], [0, 1/8, M], [1, -1, N], [-1, 1, O], [1, 1, P], [0, 1/4, Q], [1/7, 1/7, R], [-1/7, 1/7, S]

画图得到：

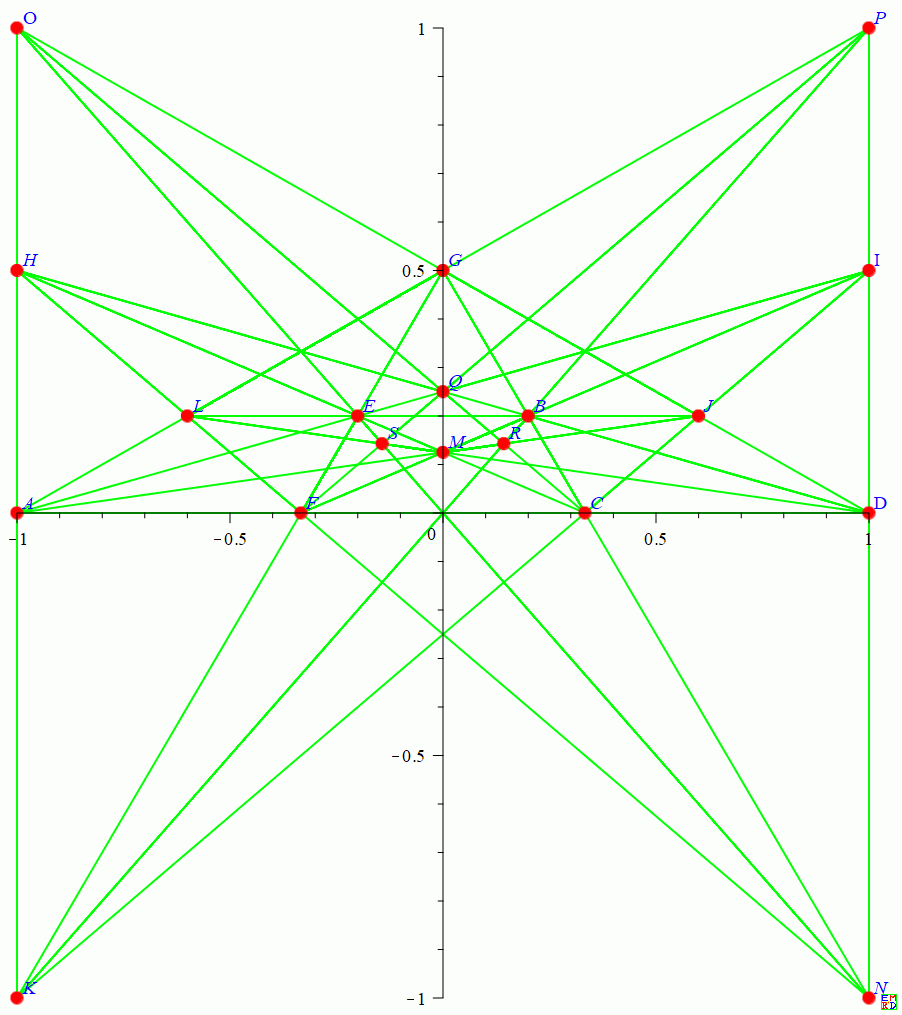
第三种

变换基点：

[1, -1, 0]-->[-1/4, sqrt(3)/6, 1]
[1, 0, 1]--> [-1/2, 0, 1]
[-1, 1, 1]--> [1/2, 0, 1]
[1, -1/4, 0]--> [1/4, sqrt(3)/6, 1]

变换矩阵

[[-1/6, 1/3, -1/6], [-1/3*sqrt(3), -2/3*sqrt(3), 1/3*sqrt(3)], [-2, -4, 8/3]]

变换后坐标

[-1/4, sqrt(3)/6, A], [1/8, sqrt(3)/4, B], [1/12, sqrt(3)/6, C], [1/4, sqrt(3)/6, D], [-1/8, sqrt(3)/4, E], [-1/12, sqrt(3)/6, F], [0, 0, G], [1/2, 0, H], [-1/2, 0, I], [3/8, sqrt(3)/4, J], [-1/16, sqrt(3)/8, K], [-3/8, sqrt(3)/4, L], [0, sqrt(3)/5, M], [1/16, sqrt(3)/8, N], [1/8, sqrt(3)/12, O], [-1/8, sqrt(3)/12, P], [0, sqrt(3)/3, Q], [1/16, (5*sqrt(3))/24, R], [-1/16, (5*sqrt(3))/24, S]

画图得到：

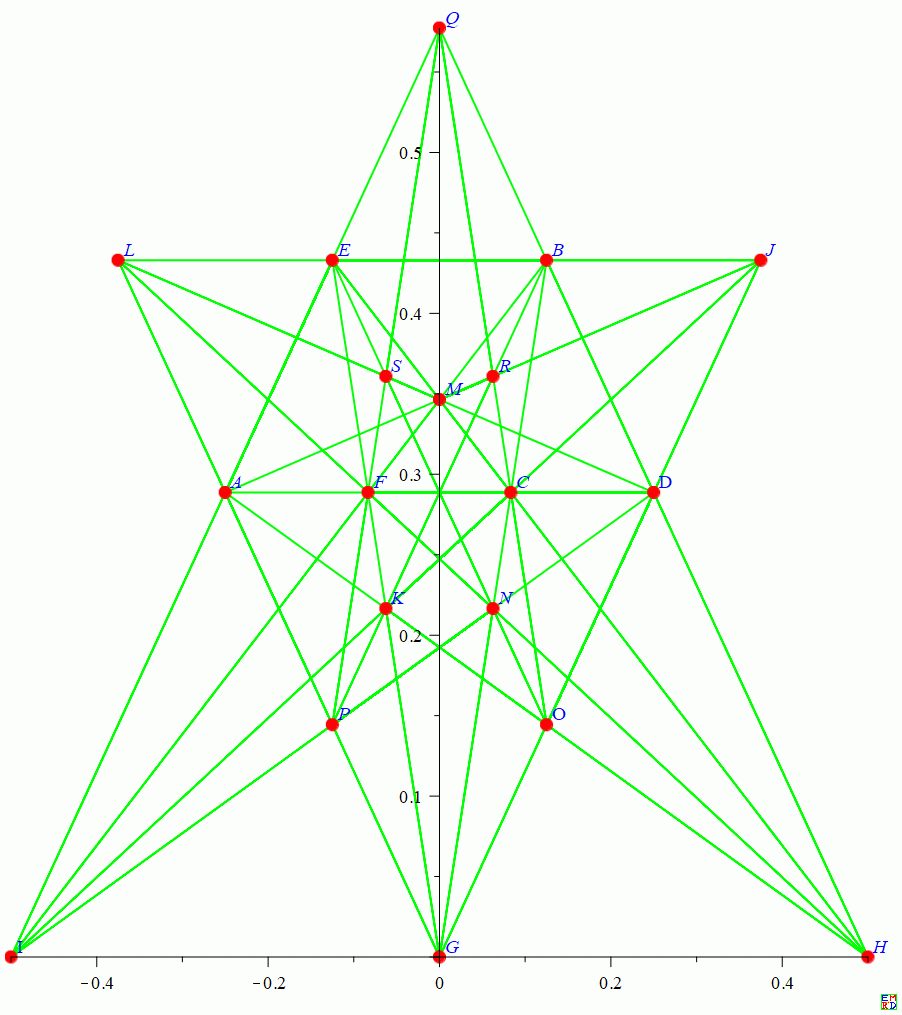
mathe · 发表于 2020-1-6 20:34:17

mathe 发表于 2020-1-6 11:43
16棵15行实数解（两个应该都具有很强的对称性）有
Parameter [+1+3*t+1*t^2=0](Real)
A[ ...

16棵15行第一个实数解为正五角星嵌套，而第二个对称解可以转化为

DFGICEHJBEIKAFJKBCGLADHLACIMBDJMCDKNEFLNAEGOBFHOGHMPABNPIJOP

数学星空 · 发表于 2020-1-6 22:42:34

16棵15行

初始数据：

[[B, C, H, I], [A, D, G, J], [B, E, G, K], [D, F, I, K], [A, F, H, L], [C, E, J, L], [C, F, G, M], [D, E, H, M], [A, E, I, N], [B, F, J, N], [A, C, K, O], [B, D, L, O], [A, B, M, P], [C, D, N, P], [E, F, O, P]]

[[A, 1 + t, -t, 1], [B, 0, 1, 0], [C, 1, 0, 0], [D, -t, 1 + t, 1], [E, 0, 0, 1], [F, 1, 1, 1], [G, 0, 1, 1], [H, 1, 2 + t, 0], [I, 1, 1 + t, 0], [J, 1, 0, 1], [K, 0, -t, 1], [L, -t, 0, 1], [M, 1 + t, 1, 1], [N, 1, 1 + t, 1], [O, -t, -t, 1], [P, 1 + t, 1 + t, 1]]

变换基点：

E[0, 0, 1]-->[0, sqrt(3)/3, 1]
B[0, 1, 0]-->[-1/2, -sqrt(3)/6, 1]
C[1, 0, 0]--> [1/2, -sqrt(3)/6, 1]
P[1 + t, 1 + t, 1]-->[0, 0, 1]

变换矩阵

[[-1/(6 + 6*t), 1/(6 + 6*t), 0], [sqrt(3)/(18 + 18*t), sqrt(3)/(18 + 18*t), -1/9*sqrt(3)], [-1/(3 + 3*t), -1/(3 + 3*t), -1/3]]

t^2 + 3*t + 1 = 0 取t=sqrt(5)/2 - 3/2

变换后坐标
[[(-2 + sqrt(5))/(sqrt(5) + 1), sqrt(3)*(-2 + sqrt(5))/(3 + 3*sqrt(5)), A], [-1/2, -sqrt(3)/6, B], [1/2, -sqrt(3)/6, C], [(2 - sqrt(5))/(sqrt(5) + 1), sqrt(3)*(-2 + sqrt(5))/(3 + 3*sqrt(5)), D], [0, sqrt(3)/3, E], [0, sqrt(3)*(sqrt(5)/2 - 3/2)/(9/2 + (3*sqrt(5))/2), F], [-1/(sqrt(5) + 1), sqrt(3)*(-2 + sqrt(5))/(3 + 3*sqrt(5)), G], [(1/2 - sqrt(5)/2)/(3 + sqrt(5)), -sqrt(3)/6, H], [-(sqrt(5)/2 - 3/2)/(sqrt(5) + 1), -sqrt(3)/6, I], [1/(sqrt(5) + 1), sqrt(3)*(-2 + sqrt(5))/(3 + 3*sqrt(5)), J], [sqrt(5)/4 - 3/4, sqrt(3)*((3*sqrt(5))/2 - 5/2)/6, K], [-sqrt(5)/4 + 3/4, sqrt(3)*((3*sqrt(5))/2 - 5/2)/6, L], [((sqrt(5)/2 - 3/2)*sqrt(5))/10, sqrt(3)*(sqrt(5)/2 - 3/2)*sqrt(5)/30, M], [-((sqrt(5)/2 - 3/2)*sqrt(5))/10, sqrt(3)*(sqrt(5)/2 - 3/2)*sqrt(5)/30, N], [0, (2 - sqrt(5))*sqrt(3)/(-15/2 + (3*sqrt(5))/2), O], [0, 0, P]]

画图得到

1615-1.1.gif

数学星空 · 发表于 2020-1-6 22:48:55

16棵15行

初始数据：

[[B, E, I, K], [D, F, G, I], [C, E, H, J], [A, F, J, K], [B, C, G, L], [A, D, H, L], [A, C, I, M], [B, D, J, M], [C, D, K, N], [E, F, L, N], [A, E, G, O], [B, F, H, O], [G, H, M, P], [A, B, N, P], [I, J, O, P]]

[[A, 1, 0, 1], [B, 0, 1, 0], [C, 0, 0, 1], [D, -1 - t, 1, 1], [E, 1, -1, 0], [F, -t, 1, 1], [G, 0, 1, 1], [H, -t, t, 1], [I, 1, 0, 0], [J, -1 - t, 1 + t, 1], [K, 1, -t, 0], [L, 0, 1 - t, 1], [M, -1 - t, 0, 1], [N, 1, -t, 1], [O, -t, 1 + t, 1], [P, 1, 1 + t, 1]]

变换基点：

A[1, 0, 1]-->[0, sqrt(3)/3, 1]
D[-1 - t, 1, 1]-->[-1/2, -sqrt(3)/6, 1]
F[-t, 1, 1]-->[1/2, -sqrt(3)/6, 1]
B[0, 1, 0]--> [0, 0, 1]

变换矩阵

[[-1/(6 + 6*t), -1/12*1/t, 1/12*(1 - t)/t], [sqrt(3)/(18 + 18*t), -1/36*sqrt(3)/t, -1/36*sqrt(3)*(t - 1)/t], [-1/(3 + 3*t), 1/6*1/t, 1/6*(-1 - 5*t)/t]]

变换后坐标
[t/(12 + 6*t), -sqrt(3)*t/(12 + 6*t), A], [-1/2, -sqrt(3)/6, B], [(t - 1)/(2 + 10*t), sqrt(3)*(t - 1)/(6 + 30*t), C], [-1/6, sqrt(3)/6, D], [(t - 1)/(6*t + 2), -sqrt(3)/6, E], [(1 - t)/(10 + 6*t), sqrt(3)*(3*t + 1)/(30 + 18*t), F], [1/10, sqrt(3)/30, G], [(t - 1)/(6 + 6*t), -sqrt(3)*(t - 1)/(6 + 6*t), H], [1/2, -sqrt(3)/6, I], [0, sqrt(3)/3, J], [(1 - t)/(6 + 2*t), -sqrt(3)/6, K], [0, 0, L], [(-1 - t)/(6*t + 2), (3*t - 1)*sqrt(3)/(18*t + 6), M], [(t - 1)/(14 + 6*t), (-3*t - 1)*sqrt(3)/(42 + 18*t), N], [1/(4 + 2*t), sqrt(3)*(1 + 2*t)/(12 + 6*t), O], [(2 + t)/(6 + 4*t), sqrt(3)*t/(18 + 12*t), P]

-1+t+t^2=0,取t=sqrt(5)/2 - 1/2

[[(sqrt(5)/2 - 1/2)/(9 + 3*sqrt(5)), -sqrt(3)*(sqrt(5)/2 - 1/2)/(9 + 3*sqrt(5)), A], [-1/2, -sqrt(3)/6, B], [(sqrt(5)/2 - 3/2)/(-3 + 5*sqrt(5)), sqrt(3)*(sqrt(5)/2 - 3/2)/(-9 + 15*sqrt(5)), C], [-1/6, sqrt(3)/6, D], [(sqrt(5)/2 - 3/2)/(3*sqrt(5) - 1), -sqrt(3)/6, E], [(3/2 - sqrt(5)/2)/(7 + 3*sqrt(5)), sqrt(3)*((3*sqrt(5))/2 - 1/2)/(21 + 9*sqrt(5)), F], [1/10, sqrt(3)/30, G], [(sqrt(5)/2 - 3/2)/(3 + 3*sqrt(5)), -sqrt(3)*(sqrt(5)/2 - 3/2)/(3 + 3*sqrt(5)), H], [1/2, -sqrt(3)/6, I], [0, sqrt(3)/3, J], [(3/2 - sqrt(5)/2)/(5 + sqrt(5)), -sqrt(3)/6, K], [0, 0, L], [(-1/2 - sqrt(5)/2)/(3*sqrt(5) - 1), ((3*sqrt(5))/2 - 5/2)*sqrt(3)/(9*sqrt(5) - 3), M], [(sqrt(5)/2 - 3/2)/(11 + 3*sqrt(5)), (-(3*sqrt(5))/2 + 1/2)*sqrt(3)/(33 + 9*sqrt(5)), N], [1/(sqrt(5) + 3), sqrt(3)*sqrt(5)/(9 + 3*sqrt(5)), O], [(3/2 + sqrt(5)/2)/(4 + 2*sqrt(5)), sqrt(3)*(sqrt(5)/2 - 1/2)/(12 + 6*sqrt(5)), P]]

画图得到

1615-2.1.gif

账号		自动登录	找回密码
密码			欢迎注册

[求助] 果树问题讨论:这两个问题等价么？

点评

点评