由三角形引导的一个几何变换——三坐标反演

数学星空

77#的计算结果是对的，

\(21521s_1^6-94102s_1^4s_2+59436s_1^3s_3+85281s_1^2s_2^2-100116s_1s_2s_3+1800s_2^3+26244s_3^2=0\)

重心坐标方程:为了与前面符号统一记\(u=x_1,v=y_1,w=z_1\)

\(16x_1^6+368x_1^5y_1+368x_1^5z_1+884x_1^4y_1^2+10896x_1^4y_1z_1+884x_1^4z_1^2-2536x_1^3y_1^3+51236x_1^3y_1^2z_1+51236x_1^3y_1z_1^2-2536x_1^3z_1^3+884x_1^2y_1^4+51236x_1^2y_1^3z_1+191385x_1^2y_1^2z_1^2+51236x_1^2y_1z_1^3+884x_1^2z_1^4+368x_1y_1^5+10896x_1y_1^4z_1+51236x_1y_1^3z_1^2+51236x_1y_1^2z_1^3+10896x_1y_1z_1^4+368x_1z_1^5+16y_1^6+368y_1^5z_1+884y_1^4z_1^2-2536y_1^3z_1^3+884y_1^2z_1^4+368y_1z_1^5+16z_1^6=0\)

\(a=1,b=1,c=1,s=\frac{\sqrt{3}}{4}\)



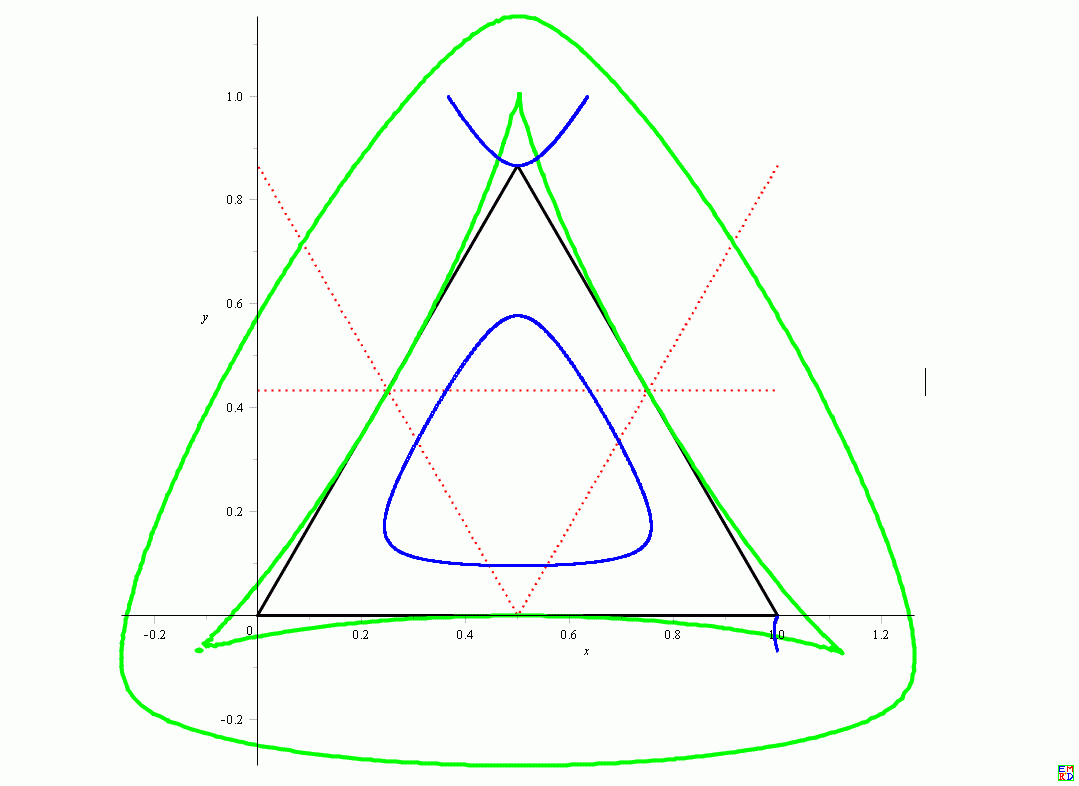
\(a=5,b=4,c=3,s=6\)




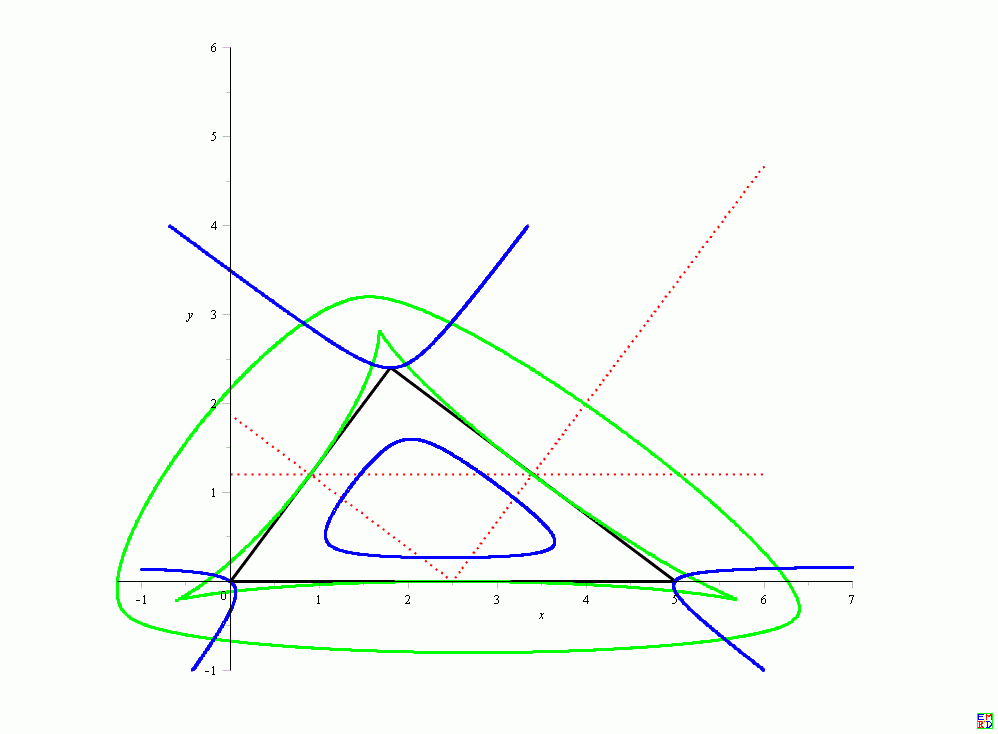
1.这样得到的结果与不动直线相切啊（红色点线）?

2.不变曲线位于三角形之外好像无法解释？

3.不变曲线从几何上如何解释：对偶不变曲线的切线包络？？

4.如何验证不变曲线的正确性？

mathe

如图
https://www.geogebra.org/classic/uhzwz5jr
拖动动点D,D点处切线为橙色虚线，此切线对应对偶三坐标反演为橙色实线。
可以看出外圈对外圈，内圈对内圈。


另外添加一个对应Geogebra文件的附件

mathe

如果将上面曲线的每条切线关于三角形外接圆做极点，那么极点描出来的曲线应该和三坐标反演对应的不变三次曲线差一个射影变换才对。而在三角形是正三角形时，两者应该相似才对。不过Geogebra做轨迹功能在使用三次以上曲线的切线后就不灵了。

mathe

为了验证上面思路，可以在上图曲线上取动点D,做D处切线关于正三角ABC外接圆极点L,然后做L关于中心O对称点并半径缩小一半到P,可以发现P会正好落在对应三坐标反演不动曲线（绿线）上。

Geogebra文件：

mathe

类似，对于给定正三角形三坐标反演的不动曲线，对上面任意一点处的切线，做起关于中心的对称直线，并平移使得距离中心距离翻倍，然后做这线关于外接圆的极点，极点轨迹就是对偶三坐标反演的不动曲线

mathe

上面方案对于等角共轭变换的对偶变化更加合适。对于等角共轭变换，即使三角形不是等边三角形，也可以通过上述方案将不变曲线变化为反演变换的不动曲线。这是因为等角共轭变换采用的坐标中，外接圆方程总是$1/x+1/y+1/z=0$,而三坐标反演只有对于正三角形外接圆方程才是如此，通常情况应该为＄a/x+b/y+c/z=0$,于是对应的极线极点直接的变换公式要复杂很多。