椭圆的周长最大内接三角形的特殊点

数学星空

关于5#提到的光反射三角形的正负Brocard 点轨迹由于与其它点的轨迹与众不同，我们可以探讨一下其轨迹方程的真面目：

光反射三角形的双椭圆为

\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)

\(\frac{x^2}{a^2-t}+\frac{y^2}{b^2-t}=1\)

\(t(a^2-b^2)^2=(2\sqrt{a^4+b^4-a^2b^2}-a^2-b^2)a^2b^2\)

设光反射三角形三点\([x_1,y_1],[x_2,y_2],[x_3,y_3]\)

\(x_1=\frac{a(1-m^2)}{1+m^2},y_1=\frac{b(2m)}{1+m^2},x_2=\frac{a(1-n^2)}{1+n^2},y_2=\frac{b(2n)}{1+n^2},x_3=\frac{a(1-p^2)}{1+p^2},y_3=\frac{b(2p)}{1+p^2}\)

正Brocard 点的坐标

\(x_0=\frac{\frac{x_1}{b_1^2}+\frac{x_2}{c_1^2}+\frac{x_3}{a_1^2}}{\frac{1}{b_1^2}+\frac{1}{c_1^2}+\frac{1}{a_1^2}}\)

\(y_0=\frac{\frac{y_1}{b_1^2}+\frac{y_2}{c_1^2}+\frac{y_3}{a_1^2}}{\frac{1}{b_1^2}+\frac{1}{c_1^2}+\frac{1}{a_1^2}}\)


负Brocard 点的坐标

\(x_0=\frac{\frac{x_1}{c_1^2}+\frac{x_2}{a_1^2}+\frac{x_3}{b_1^2}}{\frac{1}{c_1^2}+\frac{1}{a_1^2}+\frac{1}{b_1^2}}\)

\(y_0=\frac{\frac{y_1}{c_1^2}+\frac{y_2}{a_1^2}+\frac{y_3}{b_1^2}}{\frac{1}{c_1^2}+\frac{1}{a_1^2}+\frac{1}{b_1^2}}\)


\(a_1^2=(x_2-x_3)^2+(y_2-y_3)^2\)

\(b_1^2=(x_3-x_1)^2+(y_3-y_1)^2\)

\(c_1^2=(x_1-x_2)^2+(y_1-y_2)^2\)


光反射三角形有关系式：

3*b^4*m^4*n^4 + 4*a^2*b^2*m^4*n^2 + 16*a^2*b^2*m^3*n^3 + 4*a^2*b^2*m^2*n^4 - 2*b^4*m^4*n^2 - 8*b^4*m^3*n^3 - 2*b^4*m^2*n^4 + 16*a^4*m^3*n + 16*a^4*m^2*n^2 + 16*a^4*m*n^3 - 16*a^2*b^2*m^3*n - 16*a^2*b^2*m^2*n^2 - 16*a^2*b^2*m*n^3 - b^4*m^4 + 8*b^4*m^3*n + 4*b^4*m^2*n^2 + 8*b^4*m*n^3 - b^4*n^4 + 4*a^2*b^2*m^2 + 16*a^2*b^2*m*n + 4*a^2*b^2*n^2 - 2*b^4*m^2 - 8*b^4*m*n - 2*b^4*n^2 + 3*b^4=0

3*b^4*n^4*p^4 + 4*a^2*b^2*n^4*p^2 + 16*a^2*b^2*n^3*p^3 + 4*a^2*b^2*n^2*p^4 - 2*b^4*n^4*p^2 - 8*b^4*n^3*p^3 - 2*b^4*n^2*p^4 + 16*a^4*n^3*p + 16*a^4*n^2*p^2 + 16*a^4*n*p^3 - 16*a^2*b^2*n^3*p - 16*a^2*b^2*n^2*p^2 - 16*a^2*b^2*n*p^3 - b^4*n^4 + 8*b^4*n^3*p + 4*b^4*n^2*p^2 + 8*b^4*n*p^3 - b^4*p^4 + 4*a^2*b^2*n^2 + 16*a^2*b^2*n*p + 4*a^2*b^2*p^2 - 2*b^4*n^2 - 8*b^4*n*p - 2*b^4*p^2 + 3*b^4=0

3*b^4*m^4*p^4 + 4*a^2*b^2*m^4*p^2 + 16*a^2*b^2*m^3*p^3 + 4*a^2*b^2*m^2*p^4 - 2*b^4*m^4*p^2 - 8*b^4*m^3*p^3 - 2*b^4*m^2*p^4 + 16*a^4*m^3*p + 16*a^4*m^2*p^2 + 16*a^4*m*p^3 - 16*a^2*b^2*m^3*p - 16*a^2*b^2*m^2*p^2 - 16*a^2*b^2*m*p^3 - b^4*m^4 + 8*b^4*m^3*p + 4*b^4*m^2*p^2 + 8*b^4*m*p^3 - b^4*p^4 + 4*a^2*b^2*m^2 + 16*a^2*b^2*m*p + 4*a^2*b^2*p^2 - 2*b^4*m^2 - 8*b^4*m*p - 2*b^4*p^2 + 3*b^4=0

消元工作已超出了我的电脑内存

通过取{a=5,b=3}计算出了997个样本光反射三角形得到的轨迹（蓝色曲线）：





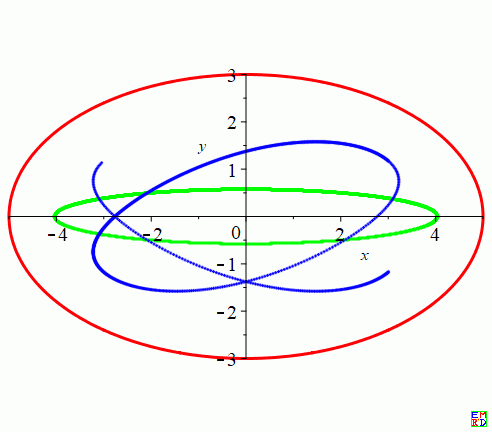
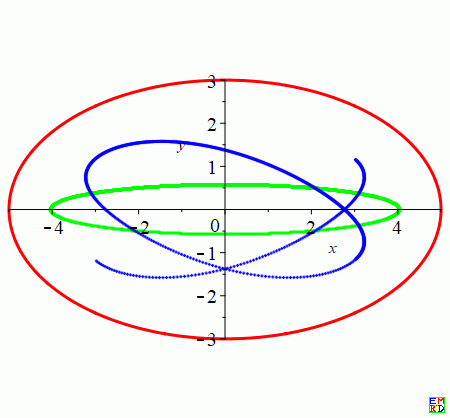
谁有兴趣计算一下具体的轨迹表达式？

数学星空

对于\(a=5,b=3\) ,我们可以算得：正负BROCARD点的轨迹方程：

5904900000000*x^32 + 94478400000000*x^30*y^2 + 708588000000000*x^28*y^4 + 3306744000000000*x^26*y^6 + 10746918000000000*x^24*y^8 + 25792603200000000*x^22*y^10 + 47286439200000000*x^20*y^12 + 67552056000000000*x^18*y^14 + 75996063000000000*x^16*y^16 + 67552056000000000*x^14*y^18 + 47286439200000000*x^12*y^20 + 25792603200000000*x^10*y^22 + 10746918000000000*x^8*y^24 + 3306744000000000*x^6*y^26 + 708588000000000*x^4*y^28 + 94478400000000*x^2*y^30 + 5904900000000*y^32 - 2063250792000000*x^30 - 23656394088000000*x^28*y^2 - 114548184072000000*x^26*y^4 - 275173641288000000*x^24*y^6 - 161915454792000000*x^22*y^8 + 1103718031416000000*x^20*y^10 + 4272750105624000000*x^18*y^12 + 8621961632856000000*x^16*y^14 + 11750387415624000000*x^14*y^16 + 11572410265416000000*x^12*y^18 + 8403378191208000000*x^10*y^20 + 4483322828712000000*x^8*y^22 + 1715642765928000000*x^6*y^24 + 446964135912000000*x^4*y^26 + 71144387208000000*x^2*y^28 + 5229117000000000*y^30 + 335550996569520000*x^28 + 2099436158118240000*x^26*y^2 + 2031418476346320000*x^24*y^4 - 17238435865761600000*x^22*y^6 - 59144220306507600000*x^20*y^8 - 25739923574360160000*x^18*y^10 + 274251230781414480000*x^16*y^12 + 869886500010675840000*x^14*y^14 + 1422088484822240400000*x^12*y^16 + 1504709748480074400000*x^10*y^18 + 1088693033734318320000*x^8*y^20 + 539288717608578240000*x^6*y^22 + 175946153937077520000*x^4*y^24 + 34206771935484000000*x^2*y^26 + 3011162311350000000*y^28 - 32909319656686627200*x^26 - 65937782363489712000*x^24*y^2 + 595903054591073376000*x^22*y^4 + 3205561665584259936000*x^20*y^6 + 8304800087896765488000*x^18*y^8 + 19101837719078017545600*x^16*y^10 + 46110959342387961408000*x^14*y^12 + 92121846467231094336000*x^12*y^14 + 130324933079045348976000*x^10*y^16 + 125545813067626298928000*x^8*y^18 + 80836127890564348972800*x^6*y^20 + 33415992022154686560000*x^4*y^22 + 8045302438634706000000*x^2*y^24 + 860003414152650000000*y^26 + 2123527034858657500944*x^24 - 1743515939739361606848*x^22*y^2 - 46682157735465846108768*x^20*y^4 - 139692528158701883910336*x^18*y^6 - 183917285791586223250320*x^16*y^8 + 212927470846722572724864*x^14*y^10 + 1941613712839357101220032*x^12*y^12 + 5203529959352826034484352*x^10*y^14 + 7795604023302464843925744*x^8*y^16 + 7114730787305578538625600*x^6*y^18 + 3938542936381797627780000*x^4*y^20 + 1220583677898079017000000*x^2*y^22 + 163051095273338756250000*y^24 - 91885973146687065306816*x^22 + 203338549981901656824192*x^20*y^2 + 1483948735564090974631488*x^18*y^4 + 2170123034864201514259200*x^16*y^6 - 11577942768396832613892480*x^14*y^8 - 74433762798082066020600576*x^12*y^10 - 175223795191630447545468288*x^10*y^12 - 202795069274835111583475712*x^8*y^14 - 105952576518744942280996800*x^6*y^16 - 1500875756774857841040000*x^4*y^18 + 21287276355051702357000000*x^2*y^20 + 6281270883542816100000000*y^22 + 2536608407982786038028960*x^20 - 4710189399138768743021376*x^18*y^2 - 27829912724557555890494304*x^16*y^4 - 12898994638098452521510656*x^14*y^6 + 697212301153132515129599296*x^12*y^8 + 2173001408592216767219987584*x^10*y^10 + 2066678143490793133429915200*x^8*y^12 + 73983129347468771474233600*x^6*y^14 - 681645432117849525378860000*x^4*y^16 - 64849465014916077189000000*x^2*y^18 + 107574180678030886912500000*y^20 - 33555751288722269959707360*x^18 - 140198090071811302839737376*x^16*y^2 + 888792812288850867753322368*x^14*y^4 + 645735999518119996414346880*x^12*y^6 - 11943184597448649924356490048*x^10*y^8 - 17206720085859916976495588544*x^8*y^10 - 38099105662704747789085904000*x^6*y^12 - 64657750121033383479074800000*x^4*y^14 - 27295857258038167963959500000*x^2*y^16 + 4876021840255554682387500000*y^18 - 408430156396382499922693704*x^16 + 12236487002193322027547578512*x^14*y^2 - 40975478853324077871189745200*x^12*y^4 - 21934667772111154542381366192*x^10*y^6 - 41699666996756494760565510720*x^8*y^8 + 810296926253767341463012199600*x^6*y^10 + 1777278276414300849639561310000*x^4*y^12 - 1638050037079618653714084250000*x^2*y^14 + 199622870257764782587253125000*y^16 + 28732437970071843485578780152*x^14 - 365162110293418102282953532104*x^12*y^2 + 1073419991706669009605858497464*x^10*y^4 + 753200417938979307626935641144*x^8*y^6 + 4316477100730455595207865122600*x^6*y^8 - 29398190169489888388123716655000*x^4*y^10 + 509955145002620363578719625000*x^2*y^12 + 2784342731840790002210715625000*y^14 - 571168252340307322730962259328*x^12 + 5453243457916066698363773065200*x^10*y^2 - 12029331609663074408687324603472*x^8*y^4 - 24170051736307730809610388496800*x^6*y^6 - 24986454997647262495919367540000*x^4*y^8 + 235955220477319379238658332750000*x^2*y^10 + 36487869580262463944563593750000*y^12 + 3745767275867385989007057975816*x^10 - 24834558843268195143187417505400*x^8*y^2 - 15556617792830857542817686908400*x^6*y^4 + 232607315215202458557082807890000*x^4*y^6 - 1188912424485395649709328331375000*x^2*y^8 + 1535490270326825082070066965625000*y^10 + 62949616932780183029774816843361*x^8 - 484438102938880834309817969722500*x^6*y^2 + 1102866287153026912594727469648750*x^4*y^4 + 2853761151440106029054767686187500*x^2*y^6 + 21905433107984402056585571672265625*y^8 - 1706303635946034795322520401800450*x^6 + 8560934928623386375832263221843750*x^4*y^2 + 5030341340677862696229651748031250*x^2*y^4 - 31837196073683508799176286783593750*y^6 + 17211204405738437213707480078205625*x^4 - 48103302624202859574960971437218750*x^2*y^2 - 114414532223930353179144676233984375*y^4 - 84307348080490550482830220105500000*x^2 + 74286612751538270319643370362500000*y^2 + 164772480904926162619915520100000000=0


画图得到：

陈九章

陈九章

陈九章

陈九章

陈九章

陈九章

★当接切△ABC的三边长（形状+大小）确定后，它的外接、内切光反射共焦椭圆也就唯一确定了。
这两个椭圆的中心为△ABC的Mittenpunkt点M，它们的焦点是一对非常重要的特殊点！
在C.Kimbenling教授的Encyclopedia of Triangle Centens(简称ETC)网站上，似乎没有。

陈九章

数学星空老师在2020年8月25日经过深入研究，发现：
椭圆的光反射三角形的正、负Brocard 点轨迹接近椭圆，但不是椭圆，其轨迹方程是2个复杂的32次方程！

陈九章