- 注册时间
- 2007-12-27
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 49492
- 在线时间
- 小时
|
 发表于 2024-2-28 10:13:19
|
显示全部楼层
发表于 2024-2-28 10:13:19
|
显示全部楼层
补充Sporadic solutions 后面的数据.
搜索32位以内数据目标已经完成.
All data between 17 digits and 30 digits are available in github download address
012:A058411
[24]471287714788971663493899^2=222112110111011100020110111110102200012010222201
[29]10000009999995510010001000001^2=100000200000010200110220220200010211120011021020002000001 (这个数据 https://www.worldofnumbers.com/threedigits.htm#z012 上已经提供)
[31]1000001099999955100100001000001^2=1000002200001120200101222222020201022120200110201200002000001
无穷模式有两类
其中第一类仅由01构成,那么01构成的数可以用参数$1=a_0\lt a_1 \lt a_2 \lt \cdots\lt a_k$表示,写成 $X=\sum_{h=0}^k 10^{a_h}$
展开后写成$X^2=\sum_{h=0}^k 10^{2a_h} + 2\sum_{0\le h_1\lt h_2\le k} 10^{a_{h_1}+a_{h_2}}$
所以如果所有的$2a_h, a_{h_1}+a_{h_2}$互不相同,就得到一个合法的解。也就是这种无穷模式所有数满足$2a_h, a_{h_1}+a_{h_2}$互不相同的序列$1=a_0\lt a_1 \lt a_2 \lt \cdots\lt a_k$对应的整数$X=\sum_{h=0}^k 10^{a_h}$。 如100000000000000101000000010001。 于是如果我们去掉末尾数不为0的人为限制并且包含数字0,那么所有不超过n位的满足这个规律的数字的数目就是A143823 (Also the number of subsets of {1..n} such that every orderless pair of (not necessarily distinct) elements has a different sum)。比如A143823[4]-A143823[3]=6, 所以正好4位的这种规律的数字有6个,分别为1000,1001,1010,1100,1011,1101.
那么是否所有仅由01构成的这种数都必须满足上面的规律呢?答案也是否定的,比如我们可以构造多项式$f(x)=x^2048 + x^1280 + x^1088 + x^1040 + x^1028 + x^1020 + x^1008 + x^960 + x^768 + 1$, 于是$f(x)^2=x^4096 + 2*x^3328 + 2*x^3136 + 2*x^3088 + 2*x^3076 + 2*x^3068 + 2*x^3056 + 2*x^3008 + 2*x^2816 + x^2560 + 2*x^2368 + 2*x^2320 + 2*x^2308 + 2*x^2300 + 2*x^2288 + 2*x^2240 + x^2176 + 2*x^2128 + 2*x^2116 + 2*x^2108 + 2*x^2096 + x^2080 + 2*x^2068 + 2*x^2060 + x^2056 + 10*x^2048 + x^2040 + 2*x^2036 + 2*x^2028 + x^2016 + 2*x^2000 + 2*x^1988 + 2*x^1980 + 2*x^1968 + x^1920 + 2*x^1856 + 2*x^1808 + 2*x^1796 + 2*x^1788 + 2*x^1776 + 2*x^1728 + x^1536 + 2*x^1280 + 2*x^1088 + 2*x^1040 + 2*x^1028 + 2*x^1020 + 2*x^1008 + 2*x^960 + 2*x^768 + 1$系数全部是1,2,10,而且系数10只有一项$x^2048$,其前一项指数次数为$x^2056$,所以我们可以看出$f(10)$是一个所有数字都是01的数字,而且$f(10)^2$所有数字都是0,1,2,但是$f(10)$不满足这里的规律。
其中第二类由014构成,总是4在中间,两边对称各分布3个1,可以写成
$1+10^a+10^{a+h}+4\times 10^{2a+h}+10^{3a+h}+10^{3a+2h}+10^{4a+2h}$
其平方展开有19项,其中一项系数为22,其余系数都是1或2,如果我们将22拆成20+2变成两个不同的次数,那么平方后的指数和系数可以如图分布
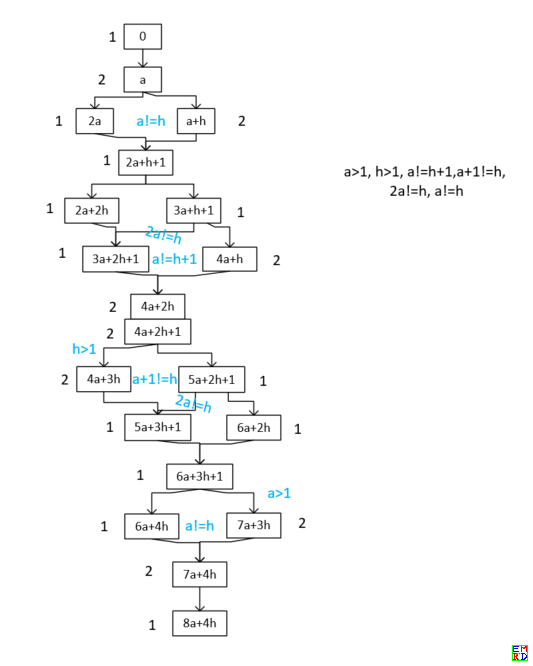
如图可以得出平方后系数都是0,1,2的一个充分条件是$a\gt 1,h\gt 1, a\ne h+1,a\ne h, a\ne h-1,2a\ne h$. 如10000010100000400000101000001。
经验证,程序找出的30位以内所有仅包含数字014的被平方数都符合这两个特征之一,所以可以认为这里已经覆盖了所有01和014模式的数。
014:A058413
其无穷模式有$10^a+2, 2\times10^a+1$, 其中$a\ge 1$,如100000000000000000000000002和20000000000000000000000001。
或者 $1+2\times 10^a+2\times10^b+10^{a+b} , 2+10^a+10^b+2\times 10^{a+b}$, 其中$b\gt a+1, a\gt 1, b\ne 2a$,如10002000000000000000020001和200000000000010010000000000002。
016:A058417
[26]77470059130002034719700749^2=6001610061606011616611060006010661000616100111161001
[31]1269252181664724031960616588454^2=1611001100660661616100110660666016660116006106161001606110116
其无穷模式有$1+3\times 10^a + 10^{2a}, 1+8\times 10^a+10^{2a}, a\ge 2$. 如100000000000030000000000001和100000000000080000000000001。
以及$4+127\times 10^{a} + 4\times 10^{2a}, a\ge 5$,如400000000001270000000000004。
018:A058421
[28]2981276371121751737986262751^2=8888008801008880800188080010010188818118011188010088001
其无穷模式有$1+9\times 10^a, 9+10^a, a\ge 2$ 以及$1+4\times 10^a +10^{2a}, a\ge 2$ 还有$1+9\times 10^a+10^{2a+1}, a\ge 2$,如
10000000000000000000000009,90000000000000000000000001和100000000000040000000000001,10000000000009000000000001。
019:A058473
[27]100990098979999970099500001^2=10199000091990191001091091099001091999900190199000001
024:A058423
[24]205524700326856587391168^2=42240402444444204240022400420200244000244404224
[27]634050802727999251005000002^2=402020420440020222440222024020044204422022004020000004
其无穷模式有$2+6\times 10^a+2\times10^{2a}, a\ge 2$,如200000000000060000000000002。
025:A058425
[24]447241797269721007814765^2=200025225225050225520202505522022522200552005225
[30]141422082876067219949805050005^2=20000205525005225202000505202222520222202205205000550500025
另外还有两组疑似规律数据,但是每组各自只有两个数,不确定是否无穷模式
[22]5000000500000500254955^2=25000005000005252550050255205255020002052025
[27]500000000000500000500254955^2=250000000000500000500255205000500255205255020002052025
[22]5000005004997549999955^2=25000050050000550000025505552050220500002025
[27]5000000500499975499999955^2=25000005005000005500225025500555205002205000002025
无穷模式比较复杂,其中第一类仅由05构成,和012:中的第一类模式类似,我们可以将它写成$\sum_{h=0}^k 5\times 10^{a_h}$,其中$1=a_0\lt a_1\lt\cdots\lt a_k$.
平方展开后各项系数分别为25和50,其中50中的10可以转移到指数,变成要求所有的$2a_h,2a_h+1, a_{h_1}+a_{h_2}+1$互不相同,或者可以改为要求所有的
$2a_h-1,2a_h,a_{h_1}+a_{h_2}$互不相同。如5000000000000000000000500505。 第一类计算机验证全部符合模式。
其中第二类由一个2和5个5和若干0构成,其中分布现在看到规律总是2前面两个5后面三个5或2前面三个5后面两个5.
我们可以假设这个数为X=5+5*10^a+5*10^b+5*10^c+5*10^d+2*10^h, 看到一类解是平方以后要求4*10^(2h)+5*10^(c+1)+5*10^(a+b+1)能够合并成5*10^(2h)
更一般情况就是要求2h-1和{a+1,b+1,c+1,d+1,a+b+1,a+c+1,a+d+1,b+c+1,b+d+1,c+d+1,0,2*a,2*b,2*c,2*d}中正好两项相同, 然后其它各项指数互不相同, 并且它们和{1,2*a+1,2*b+1,2*c+1,2*d+1}也互不相同。如50050500000002000000000505。如果我们用x表示10,可以将这个数字的平方写成
(5*x^25+5*x^22+5*x^20+2*x^12+5*x^2+5)^2=25*x^50 + 50*x^47 + 50*x^45 + 25*x^44 + 50*x^42 + 25*x^40 + 20*x^37 + 20*x^34 + 20*x^32 + 50*x^27 + 50*x^25 + 54*x^24 + 100*x^22 + 50*x^20 + 20*x^14 + 20*x^12 + 25*x^4 + 50*x^2 + 25,
其中绿色部分中4*x^24为(2*x^12)^2产生的结果,含4,正好被后面的100*x^22产生的结果叠加后将4变成5。
但是实际计算结果表明除了上面列出情况,还有一些不在这个范围,比如
500000000050205050000000005005
我们如果将上面数字中用x代表10,其平方可以写成(5*x^29+5*x^19+2*x^17+5*x^15+5*x^13+5*x^3+5)^2=25*x^58 + 50*x^48 + 20*x^46 + 50*x^44 + 50*x^42 + 25*x^38 + 20*x^36 + 54*x^34 + 120*x^32 + 45*x^30 + 50*x^29 + 50*x^28 + 25*x^26 + 50*x^22 + 20*x^20 + 50*x^19 + 50*x^18 + 20*x^17 + 50*x^16 + 50*x^15 + 50*x^13 + 25*x^6 + 50*x^3 + 25。
可以看出绿色部分的数字4对应特殊部分(2*x^17)^2, 这部分可以通过两个50*x^32产生的100*x^32叠加处理掉。但是代码里面还会产生额外的4(红色部分)为其它部分叠加的结果,又被后面一项50*x^29叠加处理掉了,这中类型前面统一的模式就处理不了了。所以第二类这部分数据特征特别复杂, 比如搜索26到30位的这类数据共217个,其中有35个不符合上面找出的规律,其它都符合。而这35种中分析了前面几种,都是额外有意向45*x^(2k)后面跟着50*x^(2k-1), 而显然其中45*x^(2k)应该来自一个(5*x^k)^2和一个2*5x^a*2x^b的叠加,比如:
- ? (+5*x^29+5*x^19+5*x^15+5*x^13+5*x^3+5*x^0+2*x^17)^2
- %3 = 25*x^58 + 50*x^48 + 20*x^46 + 50*x^44 + 50*x^42 + 25*x^38 + 20*x^36 + 54*x^34 + 120*x^32 + 45*x^30 + 50*x^29 + 50*x^28 + 25*x^26 + 50*x^22 + 20*x^20 + 50*x^19 + 50*x^18 + 20*x^17 + 50*x^16 + 50*x^15 + 50*x^13 + 25*x^6 + 50*x^3 + 25
- ? (+5*x^26+5*x^17+5*x^9+5*x^4+5*x^0+2*x^14)^2
- %4 = 25*x^52 + 50*x^43 + 20*x^40 + 50*x^35 + 25*x^34 + 20*x^31 + 50*x^30 + 4*x^28 + 100*x^26 + 20*x^23 + 50*x^21 + 45*x^18 + 50*x^17 + 20*x^14 + 50*x^13 + 50*x^9 + 25*x^8 + 50*x^4 + 25
- ? (+5*x^27+5*x^18+5*x^14+5*x^12+5*x^3+5*x^0+2*x^16)^2
- %5 = 25*x^54 + 50*x^45 + 20*x^43 + 50*x^41 + 50*x^39 + 25*x^36 + 20*x^34 + 54*x^32 + 120*x^30 + 45*x^28 + 50*x^27 + 50*x^26 + 25*x^24 + 50*x^21 + 20*x^19 + 50*x^18 + 50*x^17 + 20*x^16 + 50*x^15 + 50*x^14 + 50*x^12 + 25*x^6 + 50*x^3 + 25
- ? (+5*x^27+5*x^19+5*x^16+5*x^14+5*x^2+5*x^0+2*x^9)^2
- %6 = 25*x^54 + 50*x^46 + 50*x^43 + 50*x^41 + 25*x^38 + 20*x^36 + 50*x^35 + 50*x^33 + 25*x^32 + 50*x^30 + 50*x^29 + 45*x^28 + 50*x^27 + 20*x^25 + 20*x^23 + 50*x^21 + 50*x^19 + 54*x^18 + 100*x^16 + 50*x^14 + 20*x^11 + 20*x^9 + 25*x^4 + 50*x^2 + 25
- ? (+5*x^25+5*x^17+5*x^13+5*x^11+5*x^3+5*x^0+2*x^15)^2
- %7 = 25*x^50 + 50*x^42 + 20*x^40 + 50*x^38 + 50*x^36 + 25*x^34 + 20*x^32 + 54*x^30 + 120*x^28 + 45*x^26 + 50*x^25 + 50*x^24 + 25*x^22 + 50*x^20 + 20*x^18 + 50*x^17 + 50*x^16 + 20*x^15 + 50*x^14 + 50*x^13 + 50*x^11 + 25*x^6 + 50*x^3 + 25
其中第三类15+85*10^n+1500*10^(2n),其中$n\ge4$, 如15000000000008500000000015。
其中第四类好像$5*10^{a_0}-5\sum_{h=1}^k 10^{a_h}$,其中$a_0 \gt a_1 \gt a_2 ...\gt a_k=0$, 固体模式待确定,如44949994994999949999999995。
其中第五类和第四类相反,同样一些10的幂的5倍进行组合,但是中间有一项系数为负,其余为正,可以写成$5\sum_{h=1}^k 10^{a_h}-5*10^{a_0}$
第四第五类所有产生的指数$a_h+a_0$需要能够等于某个$a_{h_1}+a_{h_2}, h_i>0$或某个$2a_h-1$(包含$2a_0-1$), 使得出现的负参数被抵消,而余下的那些指数
包含$a_{h_1}+a_{h_2}+1, 2a_h,2a_h+1$要互不相同。 数组合模式待验证,如50000005004999999999955050005。
045:A058435
[26]21214250022106461574572502^2=450044404000444005405445044455050544404404054540004
[28]2108436491907081488939581538^2=4445504440405440505004450045555054500055550554550445444
046:A058437
无穷模式有$8+254\times 10^a+8\times 10^{2a}, a\ge 5$,如800000000002540000000000008。
048:A058441
[24]942575429577943326987798^2=888448440444044400080440444440408800048040888804
[29]20000019999991020020002000002^2=400000800000040800440880880800040844480044084080008000004
[31]2000002199999910200200002000002^2=4000008800004480800404888888080804088480800440804800008000004
和012:等价,将012:模式每个数字乘以2即可,对应无穷模式也相同,就不再列出
049:A058443
无穷模式有$10^a-3, a\ge 1$ 和$2+10^a+2\times 10^{2a}, a\ge 1$,如99999999999999999999999997和200000000000010000000000002。
067:A058499
[32]82259751809132500370470387225026^2=6766666767700077667660006767777700777007007700660707660760700676
069:A058451
[29]24691314243454114014126412353^2=609660999069000006699096996606066090996096009966990996609
089:A058455
[27]299831600904572582192518303^2=89898988900998890088080098089989880890999988989999809
124:A053880
[28]1114110597927523626433041668^2=1241242424414424212214142144114212224412421422224222224
无穷模式$\frac{10^n-1}3+5, n\ge 2$,如33333333333333333333333338
125:A031153
[28]4638162516046117503822620335^2=21512551525255251211125255525551555121211151225555512225
无穷模式$\frac{10^n-1}3+2,12\times 10^n+\frac{10^n-1}3+2, n\ge 2$ 以及$\frac{100000}3(10^n-1)+204485, n\ge 5$,如
33333333333333333333333335,12333333333333333333333335和33333333333333333333504485。
126:A053882
[26]51595698572871617009432954^2=2662116111222626216162621266666216222222216621166116
128:A053886
无穷模式$\frac{10^n-1}3+26, n\ge 3$,如33333333333333333333333359
129:A053888
[27]145303131149776986249167839^2=21112999921929291129929211912291229929191119991929921
134:A053890
[30]177324875114669443080086908188^2=31444111334433114334141133143444444313434111431113141443344
136:A053892
[29]11537606482136410218512760694^2=133116363336636111166666336113333136136363666113311361636
[32]40759430336194731508570147356619^2=1661331161331111363611616136663163363361366331311163633163111161
146:A027677
[30]105567345643273687982611367608^2=11144464466166416111166414141141166144146161144464111641664
148:A053900
[28]2209483759119790145920022988^2=4881818481814118844811411488844844184118148818448448144
156:A053902
无穷模式$\frac{10^n-1}3+1, n\ge 1$ ,如33333333333333333333334。
169:A053910
[30]248216864092061020657513399437^2=61611611619696691696969619616966119999999161919199911916969
235:A053918
[27]576387476638096486959455635^2=332222523225232223533222222253253255253352335533253225
236:A058457
[27]251462176552105392823457806^2=63233226236322223226263332266636366232262662262333636
245:A031154
[27]212706944938912242495946332^2=45244244425245444452555552444225545225555452224254224
无穷模式$\frac 2 3(10^n-1)-1, \frac{2000}3(10^n-1)+515 , 2\times 10^n + \frac{10}3(10^n-1) +5, n\ge 1$,如
66666666666666666666666665, 66666666666666666666666515,23333333333333333333333335。
246:A053922
[27]47144739098275455895604568^2=2222626424644462446266642442624422642664422222466624
[27]163176169897520398456349838^2=26626462422424442244464226222466224666246222642626244
[30]162062538622046218465618335432^2=26264266424622222222622644266266266222662426642466466626624
无穷模式$\frac{2}3(10^n-1)+2, n\ge 1$,如66666666666666666666666668。
248:A027679
[27]149140498954591218312271662^2=22242888428424424282282224442842448448442222888242244
[29]20598117118436403877526792022^2=424282428824822822284282828848288484482824448422442848484
256:A030486
[26]81401637345465395512991484^2=6626226562522666562566262626266252566552622656522256 (26位日本网站已提供)
[29]14920674457351323857264196585^2=222626526262256222655556652225555252265566656525525662225
[29]23508012597117321085533117075^2=552626656266226655522226225556662256522626266565656555625
257:A030487
[26]52174924557278712520943915^2=2722222752557725255755757775775772222257522575527225
无穷模式$10^n+\frac{2}3(10^n-1)-1, n\ge 1$, 如166666666666666666665。
259:A053928
[26]30484348812550551609088485^2=929295522525252225925225599299529559999252559595225
[26]76975943837016723668817565^2=5925295929599552922952299222959292529595925252529225
269:A053930
[26]26395073915340646948470264^2=696699926996296229992699669262629222696929692229696
279:A053932
[27]850281851974525726895170673^2=722979227797229279772792797979272222799797729799272929
289:A053934
[26]17320185602062360469701767^2=299988829289888292222928892882898892999989922922289
347:A058463
[27]271006150065722262703289312^2=73444333373444774773333473377377773344743344373433344
348:A053940
[31]2211081962399482011666571014522^2=4888883444448344384438443334848438884483434444884888334888484
369:A053948
[26]31047286456844613647179386^2=963933996333366963633963999333393696336393663336996
456:A030177
[26]25781108305591628417975738^2=664665545464645645665646644665564654546645556644644
457:A053950
[29]27341447393189418631675507588^2=747554745554544455555455747745774457774554454557445577744
[31]2185073856290801614135693743112^2=4774547757445554744745574447777547474775754757455745447444544
458:A053952
[30]293061185503724726684202222622^2= 85884858448848555885485448555548484845848584584884848554884
478:A053962
[28]6984617991328143315228383028^2=48784888484784787487448774777744787448847474447478448784
479:A053964
[27]865996535661545126193725357^2=749949999777797799497449749797947997449449477944777449
489:A053966
[26]30732718558321504090886022^2=944499989984998988844994898844848999494444994984484
[30]221018096306377014602309133712^2=48848998894894944944999998949494848849994884488899894898944
无穷模式$\frac{2}3(10^n-1)+1, n\ge 1$,如66666666666666666666666667
689:A053974
[32]99483516217346127185182923658937^2=9896969998966969889969699699898986686889966988869688899899969969
17位到27位所有结果汇总:
 runm.tgz
(79.39 KB, 下载次数: 2)
runm.tgz
(79.39 KB, 下载次数: 2)
|
评分
-
| 参与人数 2 | 威望 +16 |
金币 +16 |
贡献 +16 |
经验 +16 |
鲜花 +16 |
收起
理由
|
 王守恩 王守恩
| + 8 |
+ 8 |
+ 8 |
+ 8 |
+ 8 |
很给力! |
 northwolves northwolves
| + 8 |
+ 8 |
+ 8 |
+ 8 |
+ 8 |
威武! |
查看全部评分
|