- 注册时间
- 2008-11-26
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 149506
- 在线时间
- 小时
|
楼主 |
发表于 2016-7-6 12:23:34
|
显示全部楼层
- (*第一列乘以第二列,然后取代第二列的值*)
- Clear["Global`*"];(*Clear all variables*)
- data={{3,2.00286740806350017941198515943545931361},
- {4,1.9283589164749804283600849366519560639},
- {5,1.86400765000052485077735500471126683613},
- {6,1.81051438122816316692944707545183728148},
- {7,1.76578235001873982989444491931146614181},
- {8,1.72786431204913392367633970225491638819},
- {9,1.69526942444040933881970369205445408976},
- {10,1.66689198313550214392865903283543517526},
- {11,1.64190904616094851366101664075402220374},
- {12,1.6196998599244209974512574541584287912},
- {13,1.59978869842201869056004669676183358389},
- {14,1.58180517574496658723209695065387815411},
- {15,1.56545660481407284533740801524947779306},
- {16,1.55050851817644197976392356354789658309},
- {17,1.5367707372478112927676021766159055014},
- {18,1.52408725542126641935994748503824288176},
- {19,1.51232877977090028689582251305994783841},
- {20,1.50138715374182425550739674900868882105},
- {21,1.49117113037198696816232030789158595774},
- {22,1.481603128981051478805513257481434365},
- {23,1.47261671766567601608562219697005149641},
- {24,1.46415463821023838316030988522039252819},
- {25,1.45616724114422507854121331602445094798},
- {26,1.4486112343465122080296824494356282472},
- {27,1.44144867381000076000046233040898435983},
- {28,1.43464614322487864607990982178408997221},
- {29,1.42817408210585004403922210801221054461},
- {30,1.4220062317567129945412344765141001355},
- {31,1.41611917544533369254102429082160513084},
- {32,1.41049195445244880077344760779527345639},
- {33,1.4051057456479795593700060551553949446},
- {34,1.39994358928469090337863094895696596845},
- {35,1.39499015802841523529377394252379049117},
- {36,1.39023156004523883530353774388849366078},
- {37,1.38565517036913390218387987164360902442},
- {38,1.38124948587417599494888974270272683602},
- {39,1.37700400004464983512682767443775686515},
- {40,1.37290909442703835047823373266554024708},
- {41,1.36895594420004818247311699643331377899},
- {42,1.36513643574275156839766072988517148305},
- {43,1.36144309443977055373412981089021928638},
- {44,1.35786902125399984336720056851594591129},
- {45,1.35440783683543930473427573602498607559},
- {46,1.3510536321300155887091520853891945445},
- {47,1.34780092461321684380654451302931688756},
- {48,1.34464461940656131097555379617152740538},
- {49,1.34157997464560704966451256923364150444},
- {50,1.33860257056055295892954001842319703868}};
- (*第二列换成第一列与第二列的乘积*)
- data[[All, 2]]*=data[[All,1]];
- out=NonlinearModelFit[data,a+b*x^(1/2)+c*x, {a,b,c}, x];
- Normal[out]
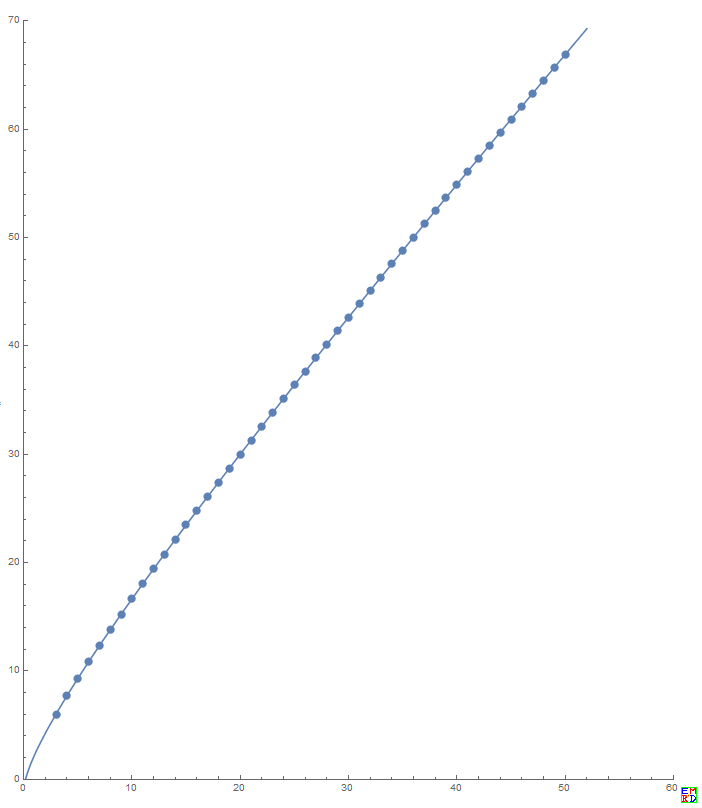
- Show[Plot[out[x],{x,0,52},PlotRange->{{0,60},{0,70}},AspectRatio->Automatic],ListPlot[data],ImageSize->800]
- Print["拟合优度值是:"];
- out["RSquared"]
拟合方程是:
-1.208100914943779516587560800750535150 + 2.42523844131677074670895367755557525 Sqrt[x] + 1.019655051803581738323392673297013864 x
拟合优度值是:
0.99999995799099676515334782556813032
|
-
|