20多年了，我无力解出来的一道高中奥数题！

数学星空

若60#的结论正确   
我们可以算出四面体各棱长：AB=ab/d, AC=ac/d, BC=bc/d, AD=a, BD=b, CD=c

倪举鹏

这个四面体体积最大的问题  在百度贴吧有过，别人给定了数值，我用P是垂心，巧妙的放进三维坐标轴最后解4次方程，是个有根式解的4次方程，最后也可得到根式的体积。这里用字母代替了，相信最后的4次方程也有根式解，只是估计结果有几页长，这里就不算了

倪举鹏

怀疑表面积最大时候，那个点不是什么特殊点，暴力求6元高次函数极值软件也没有办法……

qiao1300

如果将该题目类比到N维是否有解?

realnumber

http://kuing.orzweb.net/viewthre ... &extra=page%3D1

数学星空

根据楼上提供的链接，出于网友kuing 精彩而初等的分析特将其解答过程转载如下(图片引用原文)：

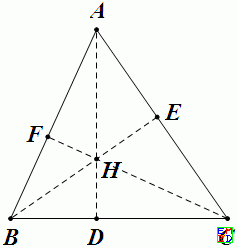
引理1：锐角\(\triangle ABC\) 中，\(H\)为其垂心，则\(AH\*HD=BH\*HE=CH\*HF=k\),

       \(\frac{k}{k+HA^2}+\frac{k}{k+HB^2}+\frac{k}{k+HC^2}=1\)

       注：1.由\(AFH \sim CDH\) 可以得到\(\frac{AH}{FH}=\frac{CH}{DH}\) 即\(AH\*HD=CH\*HF\),同理易得\(AH\*HD=BH\*HE\)

            2.\(\frac{S_{BHC}}{S_{ABC}}+\frac{S_{AHC}}{S_{ABC}}+\frac{S_{AHB}}{S_{ABC}}=1\)

              \(\frac{HD}{AH+HD}+\frac{HE}{BH+HE}+\frac{HF}{CH+HF}=1\)

             \(\frac{AH\*HD}{AH\*HD+HA^2}+\frac{BH\*HE}{BH\*HE+HB^2}+\frac{CH\*HF}{CH\*HF+HC^2}=1\)






在下面垂心四面体\(D-ABC\)的垂心\(H\)在四面体的内部，已知\(HA=a,HB=b,HC=c,HD=d\),体积为\(V\)



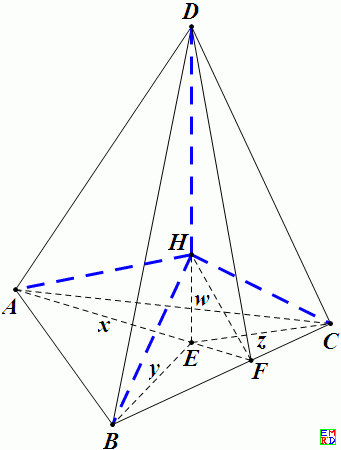
并记\(H\)在底面ABC的投影为\(E\),且记\(AE=x,BE=y,CE=z,HE=w\),由引理1，我们可以得到：

在\(\triangle ABC\) 中，设\(AE\*EF=k\),有  \(\frac{k}{k+x^2}+\frac{k}{k+y^2}+\frac{k}{k+z^2}=1\) ..........(1)

由于\(HE\perp \triangle ABC\) 易有\(x^2=a^2-w^2,y^2=b^2-w^2,z^2=c^2-w^2\)............................(2)

又\(\triangle AEH \sim \triangle DEF\), 有\(\frac{AE}{EH}=\frac{DE}{EF}\),即\(k=w(d+w)\).................(3)

将(2),(3)代入(1)并化简得到：\(3d^2w^4+2d(a^2+b^2+c^2+d^2)w^3+(a^2b^2+a^2+c^2+a^2d^2+b^2c^2+b^2d^2+c^2d^2)w^2-a^2b^2c^2=0\).......(4)

设\(\triangle ABC\) 的面积为\(S\),其外接圆直径为D,则\(x=D\cos(A),y=D\cos(B),z=D\cos(C)\),代入\(\cos(A)^2+\cos(B)^2+\cos(C)^2+2\cos(A)\cos(B)\cos(C)=1\)

得到：\(D(x^2+y^2+z^2)+2xyz=D^3\).........................................................................................(5)

又\(a^2=(D\sin(A))^2=D^2-(D\cos(A))^2=D^2-x^2\)，同理\(b^2=D^2-y^2\),\(c^2=D^2-z^2\).......(6)

代入\(16S^2=2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4\).............................................................(7)

得到：\(16S^2=3D^4-2(x^2+y^2+z^2)D^2+2(x^2y^2+x^2z^2+y^2z^2)-(x^4+y^4+z^4)\)..........(8)

将（2）代入(5)和(8)并消除\(D\)得到：

\(256S^6+16(\sum_{a,b,c}^{}(a^4-10b^2c^2)+18w^2\sum_{a,b,c}^{}(a^2)-27w^4)S^4-8(\sum_{a,b,c}^{}(a^6b^2-4a^4b^4+a^2b^6+2a^2b^2c^4)+w^2\prod_{a,b,c}{}(a^2+b^2-2c^2))S^2+\prod_{a,b,c}^{}(a^2-b^2)^2=0\)…(9)

又\(S(d+w)=3V\).............................................................................................................................(10)

将（10）代入 (9) 消除\(S\)得到：

\(186624V^6+1296(d+w)^2(\sum_{a,b,c}^{}(a^4-10b^2c^2)+18w^2\sum_{a,b,c}^{}(a^2)-27w^4)V^4-72(d+w)^4(\sum_{a,b,c}^{}(a^6b^2-4a^4b^4+a^2b^6+2a^2b^2c^4)+w^2\prod_{a,b,c}^{}(a^2+b^2-2c^2))V^2+(d+w)^6\prod_{a,b,c}^{}(a^2-b^2)^2=0\)

数学星空

楼上最后一个等式写全了即：

\((b-c)^2(b+c)^2(a-c)^2(a+c)^2(a-b)^2(a+b)^2(d+w)^6-(72(a^6b^2+a^6c^2-2a^6w^2-4a^4b^4+2a^4b^2c^2+3a^4b^2w^2-4a^4c^4+3a^4c^2w^2+a^2b^6+2a^2b^4c^2+3a^2b^4w^2+2a^2b^2c^4-12a^2b^2c^2w^2+a^2c^6+3a^2c^4w^2+b^6c^2-2b^6w^2-4b^4c^4+3b^4c^2w^2+b^2c^6+3b^2c^4w^2-2c^6w^2))V^2(d+w)^4+(1296(a^4-10a^2b^2-10a^2c^2+18a^2w^2+b^4-10b^2c^2+18b^2w^2+c^4+18c^2w^2-27w^4))V^4(d+w)^2+186624V^6=0\)

最终计算结果为：

\(-(c-d)^2(c+d)^2(b-d)^2(b+d)^2(b-c)^2(b+c)^2(a-d)^2(a+d)^2(a-c)^2(a+c)^2(a-b)^2(a+b)^2+(72a^{10}b^6c^2+72a^{10}b^6d^2-288a^{10}b^4c^4+144a^{10}b^4c^2d^2-288a^{10}b^4d^4+72a^{10}b^2c^6+144a^{10}b^2c^4d^2+144a^{10}b^2c^2d^4+72a^{10}b^2d^6+72a^{10}c^6d^2-288a^{10}c^4d^4+72a^{10}c^2d^6-144a^8b^8c^2-144a^8b^8d^2+360a^8b^6c^4-288a^8b^6c^2d^2+360a^8b^6d^4+360a^8b^4c^6-144a^8b^4c^4d^2-144a^8b^4c^2d^4+360a^8b^4d^6-144a^8b^2c^8-288a^8b^2c^6d^2-144a^8b^2c^4d^4-288a^8b^2c^2d^6-144a^8b^2d^8-144a^8c^8d^2+360a^8c^6d^4+360a^8c^4d^6-144a^8c^2d^8+72a^6b^{10}c^2+72a^6b^{10}d^2+360a^6b^8c^4-288a^6b^8c^2d^2+360a^6b^8d^4-1296a^6b^6c^6+432a^6b^6c^4d^2+432a^6b^6c^2d^4-1296a^6b^6d^6+360a^6b^4c^8+432a^6b^4c^6d^2-432a^6b^4c^4d^4+432a^6b^4c^2d^6+360a^6b^4d^8+72a^6b^2c^{10}-288a^6b^2c^8d^2+432a^6b^2c^6d^4+432a^6b^2c^4d^6-288a^6b^2c^2d^8+72a^6b^2d^{10}+72a^6c^{10}d^2+360a^6c^8d^4-1296a^6c^6d^6+360a^6c^4d^8+72a^6c^2d^{10}-288a^4b^{10}c^4+144a^4b^{10}c^2d^2-288a^4b^{10}d^4+360a^4b^8c^6-144a^4b^8c^4d^2-144a^4b^8c^2d^4+360a^4b^8d^6+360a^4b^6c^8+432a^4b^6c^6d^2-432a^4b^6c^4d^4+432a^4b^6c^2d^6+360a^4b^6d^8-288a^4b^4c^{10}-144a^4b^4c^8d^2-432a^4b^4c^6d^4-432a^4b^4c^4d^6-144a^4b^4c^2d^8-288a^4b^4d^{10}+144a^4b^2c^{10}d^2-144a^4b^2c^8d^4+432a^4b^2c^6d^6-144a^4b^2c^4d^8+144a^4b^2c^2d^{10}-288a^4c^{10}d^4+360a^4c^8d^6+360a^4c^6d^8-288a^4c^4d^{10}+72a^2b^{10}c^6+144a^2b^{10}c^4d^2+144a^2b^{10}c^2d^4+72a^2b^{10}d^6-144a^2b^8c^8-288a^2b^8c^6d^2-144a^2b^8c^4d^4-288a^2b^8c^2d^6-144a^2b^8d^8+72a^2b^6c^{10}-288a^2b^6c^8d^2+432a^2b^6c^6d^4+432a^2b^6c^4d^6-288a^2b^6c^2d^8+72a^2b^6d^{10}+144a^2b^4c^{10}d^2-144a^2b^4c^8d^4+432a^2b^4c^6d^6-144a^2b^4c^4d^8+144a^2b^4c^2d^{10}+144a^2b^2c^{10}d^4-288a^2b^2c^8d^6-288a^2b^2c^6d^8+144a^2b^2c^4d^{10}+72a^2c^{10}d^6-144a^2c^8d^8+72a^2c^6d^{10}+72b^{10}c^6d^2-288b^{10}c^4d^4+72b^{10}c^2d^6-144b^8c^8d^2+360b^8c^6d^4+360b^8c^4d^6-144b^8c^2d^8+72b^6c^{10}d^2+360b^6c^8d^4-1296b^6c^6d^6+360b^6c^4d^8+72b^6c^2d^{10}-288b^4c^{10}d^4+360b^4c^8d^6+360b^4c^6d^8-288b^4c^4d^{10}+72b^2c^{10}d^6-144b^2c^8d^8+72b^2c^6d^{10})V^2+(-1296a^8b^4+12960a^8b^2c^2+12960a^8b^2d^2-1296a^8c^4+12960a^8c^2d^2-1296a^8d^4+2592a^6b^6-18144a^6b^4c^2-18144a^6b^4d^2-18144a^6b^2c^4-38880a^6b^2c^2d^2-18144a^6b^2d^4+2592a^6c^6-18144a^6c^4d^2-18144a^6c^2d^4+2592a^6d^6-1296a^4b^8-18144a^4b^6c^2-18144a^4b^6d^2+104976a^4b^4c^4+2592a^4b^4c^2d^2+104976a^4b^4d^4-18144a^4b^2c^6+2592a^4b^2c^4d^2+2592a^4b^2c^2d^4-18144a^4b^2d^6-1296a^4c^8-18144a^4c^6d^2+104976a^4c^4d^4-18144a^4c^2d^6-1296a^4d^8+12960a^2b^8c^2+12960a^2b^8d^2-18144a^2b^6c^4-38880a^2b^6c^2d^2-18144a^2b^6d^4-18144a^2b^4c^6+2592a^2b^4c^4d^2+2592a^2b^4c^2d^4-18144a^2b^4d^6+12960a^2b^2c^8-38880a^2b^2c^6d^2+2592a^2b^2c^4d^4-38880a^2b^2c^2d^6+12960a^2b^2d^8+12960a^2c^8d^2-18144a^2c^6d^4-18144a^2c^4d^6+12960a^2c^2d^8-1296b^8c^4+12960b^8c^2d^2-1296b^8d^4+2592b^6c^6-18144b^6c^4d^2-18144b^6c^2d^4+2592b^6d^6-1296b^4c^8-18144b^4c^6d^2+104976b^4c^4d^4-18144b^4c^2d^6-1296b^4d^8+12960b^2c^8d^2-18144b^2c^6d^4-18144b^2c^4d^6+12960b^2c^2d^8-1296c^8d^4+2592c^6d^6-1296c^4d^8)V^4+(-186624a^6+279936a^4b^2+279936a^4c^2+279936a^4d^2+279936a^2b^4-3639168a^2b^2c^2-3639168a^2b^2d^2+279936a^2c^4-3639168a^2c^2d^2+279936a^2d^4-186624b^6+279936b^4c^2+279936b^4d^2+279936b^2c^4-3639168b^2c^2d^2+279936b^2d^4-186624c^6+279936c^4d^2+279936c^2d^4-186624d^6)V^6+45349632V^8=0\)

若做代换：

\(s_1 = a^2+b^2+c^2+d^2, s_2 = a^2b^2+a^2c^2+a^2d^2+b^2c^2+b^2d^2+c^2d^2, s_3 = a^2b^2c^2+a^2b^2d^2+a^2c^2d^2+b^2c^2d^2, s_4 = a^2b^2c^2d^2\)

可以将结果简化为：

\(45349632V^8+(-186624s_1^3+839808s_1s_2-5038848s_3)V^6+(15552s_1^3s_3-1296s_1^2s_2^2+7776s_1^2s_4-69984s_1s_2s_3+5184s_2^3-186624s_2s_4+209952s_3^2)V^4+(648s_1^3s_2s_4-432s_1^3s_3^2+72s_1^2s_2^2s_3-432s_1^2s_3s_4-2880s_1s_2^2s_4+1944s_1s_2s_3^2-288s_2^3s_3-6912s_1s_4^2+10368s_2s_3s_4-3888s_3^3)V^2+27s_1^4s_4^2-18s_1^3s_2s_3s_4+4s_1^3s_3^3+4s_1^2s_2^3s_4-s_1^2s_2^2s_3^2-144s_1^2s_2s_4^2+6s_1^2s_3^2s_4+80s_1s_2^2s_3s_4-18s_1s_2s_3^3-16s_2^4s_4+4s_2^3s_3^2+192s_1s_3s_4^2+128s_2^2s_4^2-144s_2s_3^2s_4+27s_3^4-256s_4^3=0\)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

最终简化结果与54#简化结果是一致的！

数学星空

根据57#，58#  mathe的结论，猜想：

当 定长\(PA ,PB, PC, PD\) 构成的四面体各条棱边长最大时即\((AB+AC+BC+DA+DB+DC)_{\max}\)，设\(\triangle ABC,\triangle DBC,\triangle DAC,\triangle DAB\)的内心分别为\(P_0,P_1,P_2,P_3\)

\(P\)点即为\(AP_1\cap BP_2 \cap CP_3  \cap DP_0\)  ？

倪举鹏

我感觉我解决了这个问题，P点不是特殊点，要想得到面积最值，只有依靠5个未知数的函数求极值了。我是拿两个长100，两个短1的TA  TB  TC TD 构成对称四面体求两个角度的方法。两个100的线夹角是2*0.7874489594，两个1线的夹角是2*0.9562693657.发现这个四面体没有什么特殊线或面的关系。大家可以用这个方法验证。如果求4个长度不一样的TA TB TC TD  估计软件能力有限。当然这个四面体会满足：每一个顶点到底面边的距离的增量，乘以各自的底边3个值会相等

倪举鹏

好了，发现这个最大体积最大表面积问题可以通过软件数值求解了。相信最长棱长也数值求解没有问题。设5个未知数，5个偏导数等于0，是可以解出来的。不要再研究满足什么条件或有根式解了，方程长度太恐怖了