A4正方形

dlpg070

dlpg070 发表于 2021-1-3 09:13
EN=15不够大,改为EN=20 ,排行表更新到附件sqrt2_1_20210101.txt
初步比较与sqrt2.out一致
最新统计 ...

一直在思考把n=17和n=27 扩展成2个混排类,分析发现:
n=17 和 n=27 排列方案的特点:

1 二者都是页面中心{1/2,Sqrt[2]/2}旋转对称
2 上下斜放正方形上下到顶
3 b 或 c的空白条,左右不靠边,最大
4 n=17单排,n=27双排,另外n=26 135#有双排例子
依以上特征可以构造新得排列方案,或构型
暂称 f17 ,f27 (Ts,Td,Tm---?)
双排还可以扩展为多排 :3排,4排,5排,---
或许将得到许多优秀解,期待sqrt.c的新版本


下面是重新整理的几个例子:
A4正方形混排_17_0_20201114.png
A4正方形混排_27_0_20201114.png
uk702135_20210114.png


A4正方形混排_17_0_20201114.png

n=17

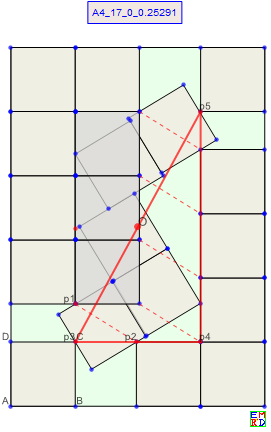
n=17图形以O={1/2,Sqrt[2]/2}为旋转中心对称,单列混排,
当时画图不严密,中间的斜放正方形应斜向移动,使O在中心

A4正方形混排_27_0_20201114.png

n=27

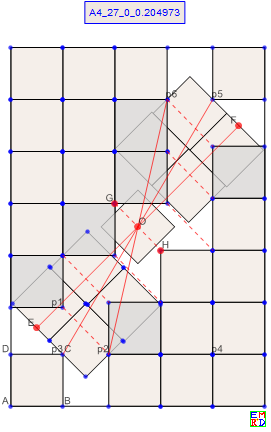
n=27图形以O={1/2,Sqrt[2]/2} 为旋转中心对称,双列混排
,OE  或EF 用于检验解的合理性 OE大于2.5a ,EF大于5 a
底部斜放正方形不靠边,

uk702135_20210114.png

n=26

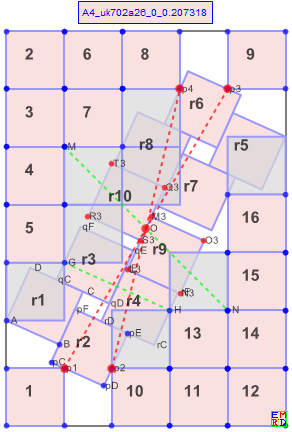
n=26图形以O={1/2,Sqrt[2]/2} 为旋转中心对称,双列混排,
与n=27的区别:底部2个斜放正方形交错,靠边

mathe

https://erich-friedman.github.io/packing/squinsqu/
这个链接里面有正方形里面放正方形的，很类似