A4正方形

mathe

稍微扩展uk702楼上的思路，可以得到
26个正方形边长0.20738797102492749613556875451171382024

b26.ggb (34.57 KB, 下载次数: 2)

2020-12-11 08:02 上传

点击文件名下载附件

mathe

上图中横向u=4个正方形，
于是左下角倾斜正方形右下边的方程为$y-a = \tan(t)(x-1+u a)$, 其对边方程为$y=a+\frac a{\cos(t)}+\tan(t)(x-1+u a)$
将x=0代入得到和左边直线接触顶点坐标为$(0, a+\frac a{\cos(t)}-\tan(t)(1-u a))$
根据对称性，右上方倾斜正方形和右边直线接触点坐标为$(1,\sqrt{2}-a-\frac a{\cos(t)}+\tan(t)(1-u a))$
于是两者差构成的向量$(1,\sqrt{2}-2a-2\frac a{\cos(t)}+2\tan(t)(1-u a))$在向量$(\cos(t),\sin(t))$上投影为$w a$,其中$w$为倾斜正方形的数目，即
$\cos(t)+\sin(t)(\sqrt{2}-2a-2\frac a{\cos(t)}+2\tan(t)(1-u a))=w a$
或者可以写成$a=\frac{\cos(t)+\sqrt{2}\sin(t)+2\sin(t)\tan(t)}{2\sin(t)+2\tan(t)+2u\sin(t)\tan(t)+w}$
函数导数等于0要求$(\sin(t)+\sqrt{2}\cos(t)+\frac{2\tan(t)}{\cos(t)})(2u\sin(t)\tan(t)+2\sin(t)+2\tan(t)+w)-(\sqrt(2)\sin(t)+\cos(t)+2\sin(t)\tan(t))(2u\sin(t)+\frac{2u\tan(t)}{\cos(t)}+2\cos(t)+\frac{2}{\cos^2(t)})=0$
于是代入u=4,w=6，就可以得出26个正方形的解对应t=0.70487729600350406841857620353927097248,a=0.20738797102492749613556875451171382024
但是使用u=5,w=7, 对应90#的37个正方形的解得出t=0.64282783148890702078725593912341525356,a=0.17947383746159583679636625723269523287没有产生更优的解

dlpg070

mathe 发表于 2020-12-11 19:27
上图中横向u=4个正方形，
于是左下角倾斜正方形右下边的方程为$y-a = \tan(t)(x-1+u a)$, 其对边方程为$y= ...

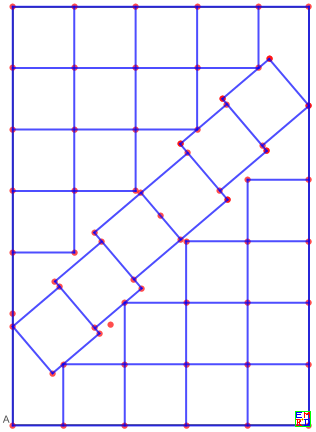
这是由141#的GGB提取数据画的图形,点线数值精度相当于double,
b26ggb提取.png
142#的公式很优秀,可做新类型加入 sqrt2.c
试算了几个数,多数得到更优解
这些解是理论的最大值,应该实际绘图验证能否实现
n=26已经绘图实现,可移动的空间很小,几乎可以确定为最优了
其他n需验证

从GGB提取数据画图

1. Clear["Global`*"];
   
2. "
   
3. n=26的各种排列的 a
   
4. 26\t{C4 4*6}\t 0.207107
   
5. 26\t{V: n=5,u=6,w=6,s=1,t=0.468518}\t 0.203552
   
6. 26\t{V: n=5,u=6,w=6,s=2,t=0.468518}\t 0.203552
   
7. 26\t{V: n=5,u=6,w=6,s=3,t=0.468518}\t 0.203552
   
8. 26\t4*6+2H\t 0.203332
   
9. 数学星空 130# :无对应排列实例
   
10.   a=0.20716844281037212074653956988084087120427093162765
    
11.   m=0.57376249355678927730002565653453480701043880740254
    
12.   n=0.5953508075350799053088957662020132353793505159293,
    
13.   t1=1.0418075270915226156504161245040707866725580121834,
    
14.   t2=1.0739879272066767994424416392246284907126061344054
    
15. mathe 138#:单排
    
16. a =0.20721104897365918253946967525090920670
    
17. t =0.73793551389460718773965984811536761268
    
18. mathe 126# 双排
    
19. a =0.207317958160075956638385951290;
    
20. t =0.423260927531078549900329777329
    
21. mathe 141#:单排
    
22. a =0.20738797102492749613556875451171382024
    
23. t =0.704877296
    
24. ***************
    
25. 26\t{C4 4*6}\t 0.207107
    
26. 37\t{Cu2 5*7} t=0.530584\t 0.180378
    
27. 42\t{Cu2 5*8} t=0.989197\t 0.168446
    
28. 56\t{Cu2 6*9} t=1.230959\t 0.146447
    
29. 72\t{Cu2 7*10} t=0.262574\t 0.130293
    
30. "
    
31. 
    
32. (*t=0.70487729600350406841857620353927097248;
    
33. a=0.20738797102492749613556875451171382024;
    
34. u=4;v=6;*)
    
35. p1= {0, a+a/Cos[t]-Tan[t]*(1-u a)};
    
36. p2={1,Sqrt[2]-a-a/Cos[t]+Tan[t]*(1-u a)};
    
37. v1={1,Sqrt[2]-2 a-2 a/Cos[t]+2 Tan[t]*(1-u a)};
    
38. v2={Cos[t],Sin[t]};
    
39. fa[u_,v_,t_]:=(Cos[t]+Sqrt[2] Sin[t]+ 2 Sin[t] Tan[t])/(2 Sin[t]+ 2 Tan[t]+ 2 u Sin[t] Tan[t]+v);
    
40. fuv[u_,v_]:=Module[{sol,t},
    
41. sol=NMaximize[{fa[u,v,t],Pi/2>t>0},t,WorkingPrecision->40];
    
42. Print["n=",u*v+2,",u=",u,",v=",v,"\na= ",sol[[1]],"\nt= ",t/.sol[[2]]]
    
43. ];
    
44. fuv[4,6]
    
45. fuv[5,7]
    
46. fuv[5,8]
    
47. fuv[6,9]
    
48. fuv[7,10]
    
49. Print[" --- end ---"]

复制代码

计算结果:

n=26的各种排列的 a
26        {C4 4*6}         0.207107
26        {V: n=5,u=6,w=6,s=1,t=0.468518}         0.203552
26        {V: n=5,u=6,w=6,s=2,t=0.468518}         0.203552
26        {V: n=5,u=6,w=6,s=3,t=0.468518}         0.203552
26        4*6+2H         0.203332
数学星空 130# :无对应排列实例
  a=0.20716844281037212074653956988084087120427093162765
  m=0.57376249355678927730002565653453480701043880740254
  n=0.5953508075350799053088957662020132353793505159293,
  t1=1.0418075270915226156504161245040707866725580121834,
  t2=1.0739879272066767994424416392246284907126061344054
mathe 138#:单排
a =0.20721104897365918253946967525090920670
t =0.73793551389460718773965984811536761268
mathe 126# 双排
a =0.207317958160075956638385951290;
t =0.423260927531078549900329777329
mathe 141#:单排
a =0.20738797102492749613556875451171382024
t =0.704877296
***************
26        {C4 4*6}         0.207107
37        {Cu2 5*7} t=0.530584         0.180378
42        {Cu2 5*8} t=0.989197         0.168446
56        {Cu2 6*9} t=1.230959         0.146447
72        {Cu2 7*10} t=0.262574         0.130293


n=26,u=4,v=6
a= 0.2073879710249274961355687545117138202431
t= 0.7048772960035040684135762020371555953442
n=37,u=5,v=7
a= 0.1794738374615958367963662572326952328712
t= 0.6428278314889070207822559386052493027745
n=42,u=5,v=8
a= 0.1688855717688902954859843941346764815879
t= 0.8152361623383266506839836706560506170416
n=56,u=6,v=9
a= 0.1494368771077263159870765260561506543783
t= 0.7377127399767251340410071245543785664328
n=72,u=7,v=10
a= 0.1342371251075505609047805060692296549461
t= 0.6909629373222724390548585716238212271763
--- end ---

uk702

我是酱掉了，不知各位前辈觉得有没有新的组合可能？

mathe

a26.ggb (33.77 KB, 下载次数: 1)

2020-12-13 08:40 上传

点击文件名下载附件

uk702这个方法很不错，随着边长的增加，可以提供更多的优秀解。

dlpg070

mathe 发表于 2020-12-13 08:41
uk702这个方法很不错，随着边长的增加，可以提供更多的优秀解。

26=4*6+2= 4*6+2对应右2图形,不是最右图形,最大区别是b 和 c 细长区域不联通,成2个 十字形区域
神了,竟然达到我认为的理论极限.
提取a26.ggb,除保存png外,保存 a26.pdf ,uk702等可在MMA中Import,编辑此文件图形元素(平移旋转复制,粘贴删除等)
a26.pdf (14.05 KB, 下载次数: 12)

2020-12-13 14:31 上传

点击文件名下载附件
可编辑

a26ggb提取.png

a26提取图形143#

uk702

dlpg070 发表于 2020-12-13 14:33
26=4*6+2= 4*6+2对应右2图形,不是最右图形,最大区别是b 和 c 细长区域不联通,成2个 十字形区域
神了, ...

相信是因为 6/4、10/7 接近 √2 的缘故，这时 uv 个正方形本身对空间的利用就比较充分了，并刚好多出能够容纳两个小正方形的空间。如果 u/v 和  √2 相差太大，uv 个正方形本身空间利用不足，若只加两个小正方形的话，空白空间的利用率偏低。

hujunhua

与145#，146#这种错开型4×6+2布置相仿的下一个应该是6×9+3,
$a=(1+\sqrt2)/(15+\sqrt2)=0.14708067207723466674091319344814$

mathe

注意到楼上右下角的4×6+2模块对应26个小正方的最优解情况，如果把这部分替换成27个小正方形已知的最优情况，并且适当调节左边三列和上面两行正方形的大小，可以得到一个58个正方形的不错的结果。

数学星空

对应148# hujunhua可以考虑更一般结论: 正规错开型\(m\*n+k\) (正方形正放和k个45度斜放类型)
\(m\geq2k,n\geq3k-1\)
\(a=\frac{1+\sqrt2}{ m+n+\sqrt2}\)