A4正方形

mathe · 发表于 2020-11-20 20:51:04

修改一个版本，会输出多个结果（保存最多5个最优结果）

sqrt2.tgz (38.86 KB, 下载次数: 11)

mathe · 发表于 2020-11-21 14:23:54

27个正方形终于构造了一个看上去对称一些的更优解

s27.ggb (41.35 KB, 下载次数: 2)
a=0.20494241311295878832697322513932693100
t=0.83642822253574782734618398153484760283
$(1-3a)sin(t)+cos(t)a/{tan(t)}=2a$
$(1-3a)sin(t)+( sqrt(2)-5a+{1-3a}/{tan(t)}-{2a}/{sin(t)})cos(t)=2a$

mathe · 发表于 2020-11-21 17:23:40

发现楼上结果竟然比74#原先不规则的27正方形的方案稍微小了一点。
但是采用74#的a和t用这种方案进行摆放，竟然也能成功，
然后才发现，楼上两个等式中的第二个等式，把a表示为t的函数，在
t=0.78539816339744830961566084581987572106, 有极大值0.20497349086650882186971984463628195770

而这时楼上第一个表达式的左边大于右边2a,说明也是一个合法的解。这才是这种方案的最优解。而这时，局部放大图后看到倾斜正方形看似落在左边边界上的点实际上会稍微落在长方行内部一点点。

s27.ggb (38.31 KB, 下载次数: 2)

dlpg070 · 发表于 2020-11-21 18:18:00

dlpg070 发表于 2020-11-19 15:43
迫不及待的走马看花浏览一遍,
介绍如下:
新sqrt.c 增加2个处理排列类型 LV,LH (粗略观察)

n=58斜排有更优解码? ,对sqrt2.out的结果验算画图后,答案是否定的

为了保证验算精度,重新计算sqrt.c得13位小数 a,t
t = 0.33417170548;
a = 0.14407638036
图形文件:
A4正方形斜排V公式探讨_58_1_20201120.png

n=58斜排没有更优解

验算5点n= 58, sub= 1:
达最大值: a Sin[t]+ 7 a Cos[t]= 1.
顶部t1点y坐标为sqrt[2]: 红点t1= {0.136106,1.41421}
顶部t2点y坐标小于sqrt[2]: 红点t2= {0.544426,1.40347}
底部b2点y坐标等于0: 红点b2= {0.455574,2.68293*10^-11}
底部b1点y坐标小于0(出界): 红点b1= {0.863894,-0.0107476}
验算结果表明:除t2外都达到极限最佳值,已无改进余地
n=58 a = 0.14407638036 可认为斜排最佳

uk702 · 发表于 2020-11-27 14:42:22

本帖最后由 uk702 于 2020-11-27 14:46 编辑

使用 mathematica 来验证 n=27 的情况。

另外请教各位老师，我下载了最新的 sqrt2.tgz，其中 sqrt2.out 关于 n=27 的数据如下：
27 4*7-1    0.202031
27 {V: n=5,u=9,w=5,s=4,t=0.435750}    0.201822
27 {V: n=6,u=3,w=7,s=1,t=0.778658}    0.201067
27 {V: n=5,u=4,w=7,s=1,t=0.406030}    0.200463
27 {V: n=5,u=4,w=7,s=2,t=0.406030}    0.200463

这是什么情况？是因为最新研究成果（如 n=27 ）尚未合入到 sqrt2.c 中吗？

uk702 · 发表于 2020-11-27 14:57:24

本帖最后由 uk702 于 2020-11-27 15:10 编辑

另外，这两个坐标点我目前是试验出来的，因此 a= 0.204214 < 0.204922，不知各位老师可有公式计算？
还有，最新的研究成果，最大边长是 0.20497349086650882186971984463628195770 还是 0.20492201311295878832697322513932693100？

uk702 · 发表于 2020-11-27 15:35:27

本帖最后由 uk702 于 2020-11-27 15:46 编辑

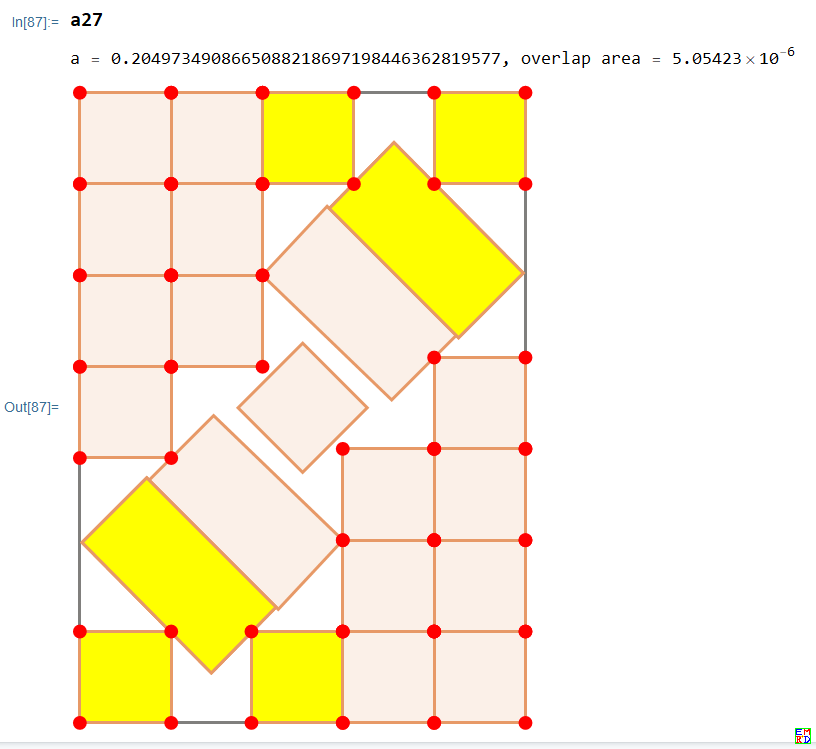
如果照搬#113 的数据作图，mathematica 显示是有重叠的。
已经没有权限上传附件了，代码就直接附加在这里。

(* n=27 的情况 *)
a27 := Module[{w, h, f, a, t, esp, sqs, ra, rb, r1, r2, r3, r4, r5},
w = 1.0; h = Sqrt[2.];
f = Rectangle[{0, 0}, {1, h}];
(* a=0.20492201311295878832697322513932693100; or a = 0.20497349086650882186971984463628195770? *)
a=0.20497349086650882186971984463628195770;
t=0.785398164;
esp = 10.0^-10;
total = 0.0;
(* 各个矩形 *)
sqs = {};
sqs = Append[sqs, Rectangle[{0, 0}, {a, a}]];
sqs = Append[sqs, Rectangle[{0, h-a}, {a, h}]];
sqs = Append[sqs, Rectangle[{0, h-2*a}, {a, h-a}]];
sqs = Append[sqs, Rectangle[{0, h-3*a}, {a, h-2*a}]];
sqs = Append[sqs, Rectangle[{0, h-4*a}, {a, h-3*a}]]; (* 5 *)
sqs = Append[sqs, Rectangle[{a, h-a}, {a*2, h}]];
sqs = Append[sqs, Rectangle[{a, h-2*a}, {a*2, h-a}]];
sqs = Append[sqs, Rectangle[{a, h-3*a}, {a*2, h-2*a}]];
sqs = Append[sqs, Rectangle[{a*2, h-a}, {a*3, h}]];
sqs = Append[sqs, Rectangle[{1-a, h-a}, {1, h}]];
sqs = Append[sqs, Rectangle[{1-3*a, 0}, {1-2*a, a}]]; (* 11 *)
sqs = Append[sqs, Rectangle[{1-2*a, 0}, {1-a, a}]];
sqs = Append[sqs, Rectangle[{1-a, 0}, {1, a}]];
sqs = Append[sqs, Rectangle[{1-2*a, a}, {1-a, 2*a}]]; (* 14 *)
sqs = Append[sqs, Rectangle[{1-a, a}, {1, 2*a}]];
sqs = Append[sqs, Rectangle[{1-2*a, 2*a}, {1-a, 3*a}]]; (* 16 *)
sqs = Append[sqs, Rectangle[{1-a, 2*a}, {1, 3*a}]];
sqs = Append[sqs, Rectangle[{1-a, 3*a}, {1, 4*a}]];
ra = Rectangle[{0, 0}, {2*a, a}];
(*
r1 = TransformedRegion[ra, RotationTransform[-t, {0, 0}]];
r1 = TransformedRegion[r1, TranslationTransform[{0, 0.434722}]];
r2 = TransformedRegion[r1, TranslationTransform[{0.166293, 0.121731}]];
*)
(* 这些数据使用的是 #113 楼 s27.ggb 的坐标 *)
r1 = Polygon[{{0.0051502184, 0.4047967633},
{0.2950265091, 0.1120494726},
{0.4399646545, 0.259858618},
{0.1500883638, 0.5497349087}}];
r2 = Polygon[{{0.1552385822, 0.5445846902},
{0.4451148729, 0.2547083995},
{0.5900530183, 0.4099469817},
{0.3001767276, 0.6895228356}}];
total += Area[RegionIntersection[r1, r2]];
(* 验证无交叠 *)
intersections = {};
For [i=1, i<=Length[sqs],
If [Area[RegionIntersection[sqs[[i]], r1]] > esp,
(* Print["Intersection: ", i, ", r1"]; *)
intersections = Append[intersections, sqs[[i]]];
intersections = Append[intersections, r1];
total += Area[RegionIntersection[sqs[[i]], r1]];
];
i = i+1];
For [i=1, i<=Length[sqs],
If [Area[RegionIntersection[sqs[[i]], r2]] > esp,
(* Print["Intersection: ", i, ", r2"]; *)
intersections = Append[intersections, sqs[[i]]];
intersections = Append[intersections, r2];
total += Area[RegionIntersection[sqs[[i]], r2]];
];
i = i+1];
(* r3、r4 与 r1、r2 对称，其实可以不再验证了 *)
r3 = TransformedRegion[r1, RotationTransform[180 Degree, {0.5, h/2}]];
r4 = TransformedRegion[r2, RotationTransform[180 Degree, {0.5, h/2}]];
total += Area[RegionIntersection[r3, r4]];
For [i=1, i<=Length[sqs],
If [Area[RegionIntersection[sqs[[i]], r3]] > esp,
(* Print["Intersection: ", i, ", r3"]; *)
intersections = Append[intersections, sqs[[i]]];
intersections = Append[intersections, r3];
total += Area[RegionIntersection[sqs[[i]], r3]];
];
i = i+1];
For [i=1, i<=Length[sqs],
If [Area[RegionIntersection[sqs[[i]], r4]] > esp,
(* Print["Intersection: ", i, ", r4"]; *)
intersections = Append[intersections, sqs[[i]]];
intersections = Append[intersections, r4];
total += Area[RegionIntersection[sqs[[i]], r4]];
];
i = i+1];
rb = Rectangle[{0, 0}, {a, a}];
r5 = TransformedRegion[rb, RotationTransform[45 Degree, {a/2, a/2}]];
r5 = TransformedRegion[r5, TranslationTransform[{0.5 - a/2, h/2 - a/2}]];
(* 验证无交叠 *)
For [i=1, i<=Length[sqs],
If [Area[RegionIntersection[sqs[[i]], r5]] > esp,
(* Print["Intersection: ", i, ", r5"]; *)
intersections = Append[intersections, sqs[[i]]];
intersections = Append[intersections, r5];
total += Area[RegionIntersection[sqs[[i]], r5]];
];
i = i+1];
total += Area[RegionIntersection[r3, r5]];
total += Area[RegionIntersection[r4, r5]];
Print["a = ", a, ", overlap area = ", total];
(* 个别验证
Print[Area[RegionIntersection[r5, r4]]];
Print[Area[RegionIntersection[r5, r3]]];
*)
(* 获取每个矩形的坐标 *)
ps = Flatten[Map[PolygonCoordinates, sqs], 1];
(* Print[ps]; *)
Graphics[{EdgeForm[{Thick, RGBColor["#807F7D"]}], White, f,
EdgeForm[{Thick, RGBColor["#E79967"]}], RGBColor["#FBF0E8"],
sqs, r1, r2, r3, r4, r5,
Yellow, intersections,
Red, PointSize[0.03], Point[ps]}]
];

复制代码

uk702 · 发表于 2020-11-27 16:51:59

本帖最后由 uk702 于 2020-11-27 16:54 编辑

Mathematica 验证 #112 楼给的数据能通过检验。
于已经无权限上传图片，图片略。

mathe · 发表于 2020-11-27 18:00:17

一些特殊解没有并入sqrt2.c

dlpg070 · 发表于 2020-11-28 19:46:05

本帖最后由 dlpg070 于 2020-11-28 19:49 编辑

uk702 发表于 2020-11-27 15:35
如果照搬#113 的数据作图，mathematica 显示是有重叠的。
已经没有权限上传附件了，代码就直接附加在这里 ...

n=27的验算,按uk702方法,修改了 r1数据 113#的a t和图形都正确,通过测试
我按公式计算
为观察覆盖,暂时去掉了显示红点,线条变细

(* 最下斜排正方形的公式  *)
n = 27;
u = 4; v = 6;
b = 1 - u a;
c = Sqrt[2] - v a;

xt = b Sin[t];
yt = b Cos[t];
pBt = {a + xt Sin[t], a - xt Cos[t]};
pAt = pBt + {-2 a  Sin[t], 2 a Cos[t]};
pCt = pBt + {a Cos[t], a Sin[t]};
pDt = pCt + {-2 a  Sin[t], 2 a Cos[t]};
r1=Polygon[{pAt,pBt,pCt,pDt}];
见图形
"A4混排a27Test_20201128.png"

n= 27
a= 0.2049734908665088218697198446362819577
b= 0.1801060365339647125211206214548721692
c= 0.1843726171740421175833696563920063324
t= 0.7853981633974483096156608458198757211
t= 45.000000000000000000000000000000000001

pAt= {0.00515021842311667607158754706107,0.404796763309900967667852142211}
pBt= {0.295026509133491178130280155364,0.114920472599526465609159533909}
PCt= {0.439964654488678429159626459515,0.259858617954713716638505838060}
pDt= {0.150088363778303927100933851212,0.549734908665088218697198446363}

账号		自动登录	找回密码
密码			欢迎注册

[讨论] A4正方形

点评

点评

点评

点评

点评