A4正方形

mathe

如果我们仅仅查看126#中第二和第三条方程，由于三个变量两条方程，我们还需要额外的极值条件。
如果选择a=0.2072,使用第二条方程，可以解得t2=1.0823532480783912061963768584031196565,
代入第三条方程，对应行列式为关于t1的一个函数，图像如下

可以看出，这时没有t1使得第三条方程成立。
而如果我们选择a=0.2071,使用第二条方程，可以解得t2=1.0583754560589007360690340217022844133
代入第三条方程，对应行列式的图像如下

所以这时可以解得t1=0.86322743127987940258188507393774721629或t1=1.2064235503364808008993124412531140525

类似如果我们修改a=0.20715,t2=1.0694919889194442972821067666160149949,
那么可以求得t1=0.94777682413999966409749131019961311368或1.1319161809545791216932267155646217128
对应26边正方形的图（中间两个正方形没有做出）

这个过程必然有一个最大的a,使得得出a,t2代入第三条方程后，行列式对应的图像和x轴相切，这代表这时这个解应该同时满足第三条方程关于t1的偏导数。
但是为什么软件求解没有找到a在0.20715和0.2072之间的解呢？

然后马上发现其实这时中间小正方形不需要使用不同的倾斜方向，所以我们可以有下图更好的结果

边长0.20731795816007595663838595129040459670

a26.ggb (45.58 KB, 下载次数: 1)

2020-12-5 07:40 上传

点击文件名下载附件

uk702

mathe 发表于 2020-12-4 07:50
如果我们仅仅查看126#中第二和第三条方程，由于三个变量两条方程，我们还需要额外的极值条件。
如果选择a= ...

n=26 才能做到 a=0.2073... 吗？我不太懂 n=26 时需要的全部约束，但如果只是求行列式的解的话，现在

a = 0.263411195766482410000000000000000000; t2 = 0.674388195727422620000000000000000000;  t1 = 0.549563195778975530000000000000000000;
求得行列式误差为 7.054261726841471997705696027840869*10^-16

另外，谁能告诉我 Mathematica 如何进行更更精度的计算，现在精确到/显示到小数点后16位后再也无法进一步提高精度，无论怎么样，后面显示的全是 0，

以下的语句，包括设置 $, $MinPrecision = 1000, $MaxPrecision = 1000，都不管用。
Print[NumberForm[det, {100, 97}], NumberForm[a, {100, 97}], NumberForm[x, {100, 97}], NumberForm[y, {100, 97}]]


实在搞不定 Mathematica 的精度，弄得每次计算出来的结果不可重复！

uk702

mathe 发表于 2020-12-4 07:50
如果我们仅仅查看126#中第二和第三条方程，由于三个变量两条方程，我们还需要额外的极值条件。
如果选择a= ...

只要是这种构图方式，a = 0.207317958160075956638385951290... 应该是到头了，不管 25 个正方形，还是 26 个正方形。
显然 GK =2 *a <= GH = Sqrt[(-1 + 3 a)^2 + (-6 a + Sqrt[2])^2]，当等号成立时，解得 a =  0.207317958160075956638385951290...

dlpg070

uk702 发表于 2020-12-4 17:07
只要是这种构图方式，a = 0.207317958160075956638385951290... 应该是到头了，不管 25 个正方形，还是 ...

分析有新意,但画图有些粗糙,斜放的正方形位置都不对
为方便你精确画图,把由a26.GGB提取的点,线的数据提供给你
说明:
1 GGB 定义了2个slider,只显示a,b未显示
   a=0.20731795816007595
   b=1.0694919889194443
2 GGB point  --->MMA Point
  GGB segment--->MMA
3 初步分析,待完善
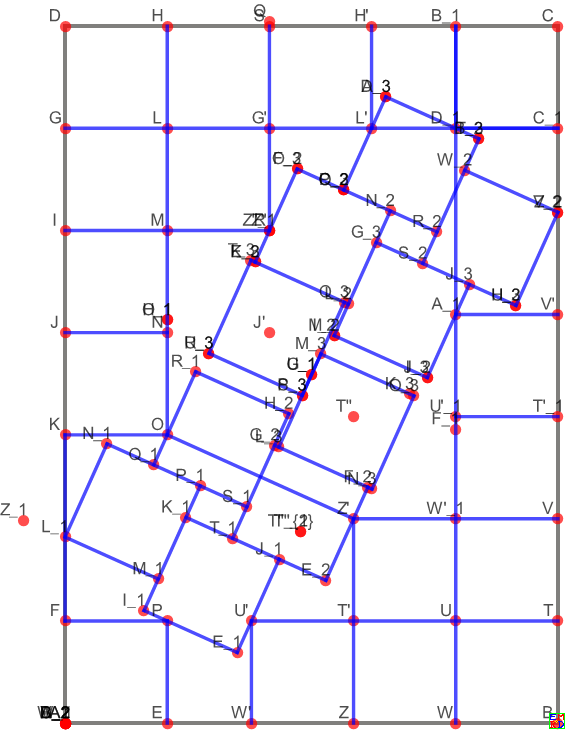
用提取数据重画的图形:
a26ggb提取.png
  

由GGB提取画图

pts=(* 序号 ,label, 显示obj, 显示label, x,y *)
{{1,A,true,false,0,0},{2,B,true,false,1.0000000000000000,0},{3,C,true,false,1.0000000000000000,1.4142135623730951},{4,D,true,false,0,1.4142135623730951},{5,E,true,false,0.20731795816007598,0},{6,F,true,false,0,0.20731795816007595},{7,G,true,false,0,1.2068956042130188},{8,H,true,false,0.20731795816007614,1.4142135623730951},{9,I,true,false,0,0.99957764605294208},{10,J,true,false,0,0.79225968789286532},{11,K,true,false,0,0.58494172973278855},{12,L,true,false,0.20731795816007615,1.2068956042130188},{13,M,true,false,0.20731795816007615,0.99957764605294210},{14,N,true,false,0.20731795816007615,0.79225968789286536},{15,O,true,false,0.20731795816007615,0.58494172973278861},{16,P,true,false,0.20731795816007615,0.20731795816007596},{17,G',true,false,0.41463591632015229,1.2068956042130188},{18,J',false,false,0.41463591632015231,0.79225968789286554},{19,Q,false,false,0.41463591632015229,1.4239023017084245},{20,R,true,false,0.41463591632015237,0.99957764605294210},{21,S,true,false,0.41463591632015235,1.4142135623730950},{22,L',true,false,0.62195387448022850,1.2068956042130188},{23,H',true,false,0.62195387448022854,1.4142135623730947},{24,T,true,false,1.0000000000000000,0.20731795816007593},{25,U,true,false,0.79268204183992419,0.20731795816007595},{26,V,true,false,1.0000000000000000,0.41463591632015179},{27,T',true,false,0.58536408367984847,0.20731795816007599},{28,T'_1,true,false,1.0000000000000000,0.62195387448022763},{29,W,true,false,0.79268204183992420,0},{30,U',true,false,0.37804612551977279,0.20731795816007600},{31,Z,true,false,0.58536408367984854,0},{32,W',true,false,0.37804612551977276,0},{33,Z',true,false,0.58536408367984839,0.41463591632015193},{34,W'_1,true,false,0.79268204183992420,0.41463591632015191},{35,U'_1,true,false,0.79268204183992419,0.62195387448022788},{36,A_1,true,false,0.79268204183992420,0.82927183264030383},{37,V',true,false,1.0000000000000000,0.82927183264030346},{38,B_1,true,false,0.79268204183992386,1.4142135623730951},{39,C_1,true,false,1.0000000000000000,1.2068956042130188},{40,D_1,true,false,0.79268204183992413,1.2068956042130187},{41,U_1,false,false,0.50000000000000000,0.70710678118654757},{42,T'',false,false,0.58536408367984825,0.62195387448022796},{43,T''_1,false,false,0.47767687409614424,0.38912678554140736},{44,Z'',true,false,0.41463591632015161,0.99957764605294320},{45,Z''_1,true,false,0.41463591632015161,0.99957764605294320},{46,F_1,true,false,0.79268204183992419,0.59644474370148348},{47,G_1,true,false,0.50000000000000000,0.70710678118654757},{48,H_1,true,false,0.20731795816007581,0.81776881867161166},{49,O_1,true,false,0.20731795816007581,0.81776881867161166},{50,Z_1,false,false,-0.083497415545819423,0.41173421639903734},{51,T''_{2},false,false,0.47767687409614424,0.38912678554140736},{52,V_1,true,false,0,0},{53,W_1,true,false,0,0},{54,A_2,true,false,0,0},{55,B_2,true,false,0,0},{56,C_2,true,false,0,0},{57,D_2,true,false,0,0},{58,E_1,true,false,0.34924361875870991,0.14338193702206286},{59,I_1,true,false,0.16022055599882332,0.22853484372838140},{60,J_1,true,false,0.43439652546502844,0.33240499978194948},{61,K_1,true,false,0.24537346270514187,0.41755790648826805},{62,L_1,true,false,0,0.37762377157271418},{63,M_1,true,false,0.18902306275988666,0.29247086486639561},{64,N_1,true,false,0.085152906706318560,0.56664683433260088},{65,P_1,true,false,0.27417596946620525,0.48149392762628230},{66,Q_1,true,false,0.17985697962330686,0.52398364303698262},{67,R_1,true,false,0.26500988632962530,0.71300670579686898},{68,S_1,true,false,0.36888004238319344,0.43883073633066416},{69,T_1,true,false,0.34007753562213006,0.37489471519264983},{70,E_2,true,false,0.52910059838201567,0.28974180848633174},{71,F_2,true,false,0.61425350508833421,0.47876487124621819},{72,G_2,true,false,0.42523044232844858,0.56391777795253628},{73,H_2,true,false,0.45403294908951194,0.62785379909055054},{74,I_2,true,false,0.54596705091048806,0.78635976328254461},{75,J_2,true,false,0.73499011367037470,0.70120685657622617},{76,K_2,true,false,0.38574649491166579,0.93544869112687690},{77,L_2,true,false,0.57476955767155148,0.85029578442055894},{78,M_2,true,false,0.54596705091048806,0.78635976328254461},{79,N_2,true,false,0.65992246437786994,1.0393188471804453},{80,O_2,true,false,0.47089940161798433,1.1244717538867632},{81,P_2,true,false,0.56560347453497162,1.0818085625911458},{82,Q_2,true,false,0.56560347453497162,1.0818085625911458},{83,R_2,true,false,0.75462653729485813,0.99665565588482704},{84,S_2,true,false,0.72582403053379475,0.93271963474681279},{85,T_2,true,false,0.83977944400117666,1.1856787186447137},{86,U_2,true,false,0.91484709329368141,0.84756672804049427},{87,V_2,true,false,1.0000000000000000,1.0365897908003810},{88,W_2,true,false,0.81097693724011334,1.1217426975066994},{89,Z_2,true,false,1.0000000000000000,1.0365897908003810},{90,A_3,true,false,0.65075638124129009,1.2708316253510323},{91,B_3,true,false,0.83977944400117666,1.1856787186447137},{92,C_3,true,false,0.56560347453497162,1.0818085625911458},{93,D_3,true,false,0.65075638124129009,1.2708316253510323},{94,E_3,true,false,0.38574649491166579,0.93544869112687690},{95,F_3,true,false,0.47089940161798433,1.1244717538867632},{96,G_3,true,false,0.63111995761680650,0.97538282604243098},{97,H_3,true,false,0.91484709329368141,0.84756672804049427},{98,I_3,true,false,0.73499011367037470,0.70120685657622617},{99,J_3,true,false,0.82014302037669314,0.89022991933611247},{100,K_3,false,false,0.69940641179465279,0.66778793400610492},{101,L_3,true,false,0.43376320965226442,0.56007385579159547},{102,M_3,true,false,0.51891611635858319,0.74909691855148225},{103,N_3,true,false,0.62278627241215068,0.47492094908527721},{104,O_3,true,false,0.70793917911846927,0.66394401184516404},{105,P_3,true,false,0.48108388364141681,0.66511664382161286},{106,Q_3,true,false,0.56623679034773558,0.85413970658149973},{107,R_3,true,false,0.29206082088153073,0.75026955052793117},{108,S_3,true,false,0.48108388364141681,0.66511664382161286},{109,T_3,true,false,0.37721372758784932,0.93929261328781788},{110,U_3,true,false,0.29206082088153073,0.75026955052793117}}
lines=
{Line[{{0,1.4142135623730951},{0,0}}],Line[{{0,0},{1.0000000000000000,0}}],Line[{{1.0000000000000000,0},{1.0000000000000000,1.4142135623730951}}],Line[{{1.0000000000000000,1.4142135623730951},{0,1.4142135623730951}}],Line[{{0,0.58494172973278855},{0.20731795816007615,0.58494172973278861}}],Line[{{0.41463591632015237,0.99957764605294210},{0.41463591632015235,1.4142135623730950}}],Line[{{0.20731795816007614,1.4142135623730951},{0.20731795816007615,0.58494172973278861}}],Line[{{0,0.79225968789286532},{0.20731795816007615,0.79225968789286536}}],Line[{{0,0.99957764605294208},{0.41463591632015237,0.99957764605294210}}],Line[{{0.62195387448022850,1.2068956042130188},{0.62195387448022854,1.4142135623730947}}],Line[{{0,1.2068956042130188},{0.41463591632015229,1.2068956042130188}}],Line[{{0.41463591632015229,1.2068956042130188},{0.62195387448022850,1.2068956042130188}}],Line[{{0.20731795816007615,0.20731795816007596},{0.20731795816007598,0}}],Line[{{0.37804612551977276,0},{0.37804612551977279,0.20731795816007600}}],Line[{{0.20731795816007615,0.20731795816007596},{0,0.20731795816007595}}],Line[{{0.37804612551977279,0.20731795816007600},{1.0000000000000000,0.20731795816007593}}],Line[{{0.58536408367984854,0},{0.58536408367984839,0.41463591632015193}}],Line[{{0.58536408367984839,0.41463591632015193},{1.0000000000000000,0.41463591632015179}}],Line[{{0.79268204183992420,0},{0.79268204183992419,0.62195387448022788}}],Line[{{0.79268204183992419,0.62195387448022788},{1.0000000000000000,0.62195387448022763}}],Line[{{0.79268204183992419,0.62195387448022788},{0.79268204183992420,0.82927183264030383}}],Line[{{0.79268204183992420,0.82927183264030383},{1.0000000000000000,0.82927183264030346}}],Line[{{1.0000000000000000,1.2068956042130188},{0.62195387448022850,1.2068956042130188}}],Line[{{0.79268204183992386,1.4142135623730951},{0.79268204183992420,0.82927183264030383}}],Line[{{0.79268204183992386,1.4142135623730951},{0.79268204183992413,1.2068956042130187}}],Line[{{0.79268204183992413,1.2068956042130187},{1.0000000000000000,1.2068956042130188}}],Line[{{0.20731795816007615,0.58494172973278861},{0.58536408367984839,0.41463591632015193}}],Line[{{0,0.58494172973278855},{0,0.20731795816007595}}],Line[{{0.34924361875870991,0.14338193702206286},{0.16022055599882332,0.22853484372838140}}],Line[{{0.18902306275988666,0.29247086486639561},{0,0.37762377157271418}}],Line[{{0.085152906706318560,0.56664683433260088},{0,0.37762377157271418}}],Line[{{0.27417596946620525,0.48149392762628230},{0.16022055599882332,0.22853484372838140}}],Line[{{0.43439652546502844,0.33240499978194948},{0.34924361875870991,0.14338193702206286}}],Line[{{0.43439652546502844,0.33240499978194948},{0.24537346270514187,0.41755790648826805}}],Line[{{0.52910059838201567,0.28974180848633174},{0.43439652546502844,0.33240499978194948}}],Line[{{0.36888004238319344,0.43883073633066416},{0.085152906706318560,0.56664683433260088}}],Line[{{0.26500988632962530,0.71300670579686898},{0.17985697962330686,0.52398364303698262}}],Line[{{0.61425350508833421,0.47876487124621819},{0.42523044232844858,0.56391777795253628}}],Line[{{0.45403294908951194,0.62785379909055054},{0.26500988632962530,0.71300670579686898}}],Line[{{0.45403294908951194,0.62785379909055054},{0.34007753562213006,0.37489471519264983}}],Line[{{0.61425350508833421,0.47876487124621819},{0.52910059838201567,0.28974180848633174}}],Line[{{0.54596705091048806,0.78635976328254461},{0.73499011367037470,0.70120685657622617}}],Line[{{0.38574649491166579,0.93544869112687690},{0.57476955767155148,0.85029578442055894}}],Line[{{0.54596705091048806,0.78635976328254461},{0.65992246437786994,1.0393188471804453}}],Line[{{0.47089940161798433,1.1244717538867632},{0.56560347453497162,1.0818085625911458}}],Line[{{0.56560347453497162,1.0818085625911458},{0.75462653729485813,0.99665565588482704}}],Line[{{0.72582403053379475,0.93271963474681279},{0.83977944400117666,1.1856787186447137}}],Line[{{0.91484709329368141,0.84756672804049427},{1.0000000000000000,1.0365897908003810}}],Line[{{0.81097693724011334,1.1217426975066994},{1.0000000000000000,1.0365897908003810}}],Line[{{0.65075638124129009,1.2708316253510323},{0.83977944400117666,1.1856787186447137}}],Line[{{0.56560347453497162,1.0818085625911458},{0.65075638124129009,1.2708316253510323}}],Line[{{0.38574649491166579,0.93544869112687690},{0.47089940161798433,1.1244717538867632}}],Line[{{0.63111995761680650,0.97538282604243098},{0.91484709329368141,0.84756672804049427}}],Line[{{0.73499011367037470,0.70120685657622617},{0.82014302037669314,0.89022991933611247}}],Line[{{0.62278627241215068,0.47492094908527721},{0.61425350508833421,0.47876487124621819}}],Line[{{0.62278627241215068,0.47492094908527721},{0.70793917911846927,0.66394401184516404}}],Line[{{0.70793917911846927,0.66394401184516404},{0.51891611635858319,0.74909691855148225}}],Line[{{0.51891611635858319,0.74909691855148225},{0.43376320965226442,0.56007385579159547}}],Line[{{0.48108388364141681,0.66511664382161286},{0.56623679034773558,0.85413970658149973}}],Line[{{0.29206082088153073,0.75026955052793117},{0.48108388364141681,0.66511664382161286}}],Line[{{0.37721372758784932,0.93929261328781788},{0.29206082088153073,0.75026955052793117}}],Line[{{0.38574649491166579,0.93544869112687690},{0.37721372758784932,0.93929261328781788}}]}

uk702

dlpg070 发表于 2020-12-5 10:14
分析有新意,但画图有些粗糙,斜放的正方形位置都不对
为方便你精确画图,把由a26.GGB提取的点,线的数据 ...

n=26 时我个人觉得已经没什么招了，想改为尝试改善 n=25 的情况。

这时 GH 要能够排列 3 个小正方形，假设 H 的坐标为 {1-a, 3a-m*a}，因此，必须有 EuclideanDistance[G,H] >= 3a，Solve[EuclideanDistance[G,H]==3*a]，解得 m→0.19233210366681976732550681，代入，得 H 坐标为
{0.79268204183992404336161404871,0.582079975459390737912459267}

其倾角为：
a=0.207317958160075956638385951290;h=Sqrt[2]; G={a, h-3*a};
H={0.7926820418399240433616140487, 0.582079975459390737912459267};
t=ArcTan[(h-3*a-0.582079975459390737912459267)/(0.7926820418399240433616140487 - a)]; 求得：t=0.34472149047858860338673920

J 点的坐标为：H - a*{Sin[t], Cos[t]}
= {0.722622137695431896370256847,0.38695861423277470900471656}

由于
J2=H-2*a*{Sin[t],Cos[t]}={0.652562233550939749378899646,0.19183725300615868009697386}
所以，直接拉2个单位的话，就会与底下的那排正方形冲突。

K 点为过 J2 作 GH 的平行线与直线 y=a 的交点。
l1=InfiniteLine[{J2,J2-{Cos[t],-Sin[t]}}];l2=InfiniteLine[{{0,a},{a,a}}];
K=RegionIntersection[l1,l2][[1]]
解得：K= {0.6094474691323290055078487,0.20731795816007595663838595129}

L 点的坐标为：L=K+3*a*{- Cos[t],Sin[t]}
解得：L= {0.0240833854524809187846206,0.417497670593552397612457555}

mathe

16个正方形除了69#的排列方式，还可以

a16.ggb (31.73 KB, 下载次数: 0)

2020-12-5 16:25 上传

点击文件名下载附件

两者边长相同，但是这个结果和70#中17个正方形的方案更加接近

uk702

uk702 发表于 2020-12-5 10:49
n=26 时我个人觉得已经没什么招了，想改为尝试改善 n=25 的情况。

这时 GH 要能够排列 3 个小正方形 ...

@dlpg070 是这样的，中间那张图不是程序生成的，而是手工编辑出来的，Mathematica 支持双击某个图元，然后复制、删除、拖动、旋转（刚发现也能旋转，当保存成 nb 文件时，还能将修改后的图形保存下来，这就方便了），就这样改出来，我觉得这样探测空隙是否有足够空间的一个好办法。

uk702

n=26 时，不知这种情况下大伙是否计算过能否提供 a > 0.207317958160075956638385951... 的边长，从图上来看可能在毫厘之间。

1. (* a262start，尝试放 26 个 *)
   
2. 
   
3. 
   
4. [code](* a262start，尝试放 26 个 *)
   
5. a262 := Module[{$MinPrecision = 50, $MaxPrecision = 50, w, h, f, a, esp, sqs, ra, rb, r1, r2, r3},
   
6. w = 1.0; h = Sqrt[2.];
   
7. f = Rectangle[{0, 0}, {1, h}];
   
8. (* a=0.211520823989986052222250797555493157307027099075156414441346; *)
   
9. a=0.207317958160075956638385951290;
   
10. esp = 10.0^-10;
    
11. total = 0.0;
    
12. 
    
13. (* 各个矩形 *)
    
14. sqs = {}; intersections={};
    
15. 
    
16. (* 底下第一排 *)
    
17. sqs = Append[sqs, Rectangle[{0, 0}, {a, a}]];
    
18. sqs = Append[sqs, Rectangle[{1-3*a, 0}, {1-2*a, a}]];
    
19. sqs = Append[sqs, Rectangle[{1-2*a, 0}, {1-a, a}]];
    
20. sqs = Append[sqs, Rectangle[{1-a, 0}, {1, a}]];
    
21. 
    
22. (* 底下第二排 *)
    
23. sqs = Append[sqs, Rectangle[{0, h-5*a}, {a, h-4*a}]];
    
24. (* sqs = Append[sqs, Rectangle[{a, a}, {2*a, 2*a}]]; *)
    
25. sqs = Append[sqs, Rectangle[{1-2*a, a}, {1-a, 2*a}]];
    
26. sqs = Append[sqs, Rectangle[{1-a, a}, {1, 2*a}]];
    
27. 
    
28. (* 底下第三排 *)
    
29. sqs = Append[sqs, Rectangle[{0, h-4*a}, {a, h-3*a}]];
    
30. sqs = Append[sqs, Rectangle[{a, h-4*a}, {2*a, h-3*a}]];
    
31. sqs = Append[sqs, Rectangle[{1-a, 2*a}, {1, 3*a}]];
    
32. 
    
33. (* 第四排 *)
    
34. sqs = Append[sqs, Rectangle[{0, h-3*a}, {a, h-2*a}]];
    
35. sqs = Append[sqs, Rectangle[{a, h-3*a}, {2*a, h-2*a}]];
    
36. sqs = Append[sqs, Rectangle[{2*a, h-3*a}, {3*a, h-2*a}]];
    
37. (* sqs = Append[sqs, Rectangle[{1-a, h-3*a}, {1, h-2*a}]]; *)
    
38. 
    
39. (* 第五排 *)
    
40. sqs = Append[sqs, Rectangle[{0, h-2*a}, {a, h-a}]];
    
41. sqs = Append[sqs, Rectangle[{a, h-2*a}, {2*a, h-a}]];
    
42. sqs = Append[sqs, Rectangle[{2*a, h-2*a}, {3*a, h-a}]];
    
43. sqs = Append[sqs, Rectangle[{3*a, h-2*a}, {4*a, h-a}]];
    
44. 
    
45. (* 第六排 *)
    
46. sqs = Append[sqs, Rectangle[{0, h-a}, {a, h}]];
    
47. sqs = Append[sqs, Rectangle[{a, h-a}, {2*a, h}]];
    
48. sqs = Append[sqs, Rectangle[{2*a, h-a}, {3*a, h}]];
    
49. sqs = Append[sqs, Rectangle[{3*a, h-a}, {4*a, h}]];
    
50. 
    
51. G = {2*a, h-4*a}; H = {1-2*a, 2*a};
    
52. 
    
53. (* 过 w1 作 GH 的平行线 l1，过 G 点作 l1 的垂线 l2 *)
    
54. w1 = {(2*a + 1 - a)/2, (h-3*a + 2*a)/2};
    
55. p1 = w1 + a*(G-H)/2/EuclideanDistance[G, H];
    
56. p2 = w1 - a*(G-H)/2/EuclideanDistance[G, H];
    
57. 
    
58. v = RotationTransform[90 Degree, {0, 0}][p2 - p1];
    
59. p3 = p1 + v;
    
60. p4 = p2 + v;
    
61. r0 = Polygon[{p1, p3, p4, p2}];
    
62. r1 = TransformedRegion[r0, TranslationTransform[{0.023, 0.039}]];   (* 暂时手工写一个 *)
    
63. r2 = TransformedRegion[r1, TranslationTransform[v]];
    
64. r3 = TransformedRegion[r1, TranslationTransform[-v]];
    
65. r4 = TransformedRegion[r1, TranslationTransform[-2*v]];
    
66. r5 = TransformedRegion[r1, TranslationTransform[-3*v]];
    
67. 
    
68. (* 语句后面不能加 ; ，否则相当于静默不显示图形 *)
    
69. Graphics[{EdgeForm[{Thin, RGBColor["#807F7D"]}], White, f,
    
70.     EdgeForm[{Thin, RGBColor["#E79967"]}], RGBColor["#FBF0E8"],
    
71.         sqs, r1, r2, r3, r4, r5
    
72.     (* Yellow, r1, *)
    
73.     (* Blue, l1, l2 *)
    
74.     (* Red, PointSize[0.03], Point[{w1}] *)
    
75.     }]
    
76. 
    
77. ]; a262
    
78. 
    
79. (* a262end *)

复制代码

mathe

上面方案在正方形倾斜角度为0.73793551389460718773965984811536761268时，达到边长最大上限0.20721104897365918253946967525090920670。
过(a,a)的正方形一条边的方程为$y-a = -ctan(t)(x-a)$, 于是平移后得到右上方倾斜正方形最上方边方程为$y-a = -ctan(t)(x-a)+\frac{5a}{\sin(t)}$
将x=1代入得到倾斜正方形和最右边边界接触点坐标为$(1,a-ctan(t)(1-a)+\frac{5a}{\sin(t)})$.
这个点和坐标$(4a, \sqrt(2)-2a)$连线在$(-\sin(t),\cos(t))$方向投影为a得到方程$(1-4a)\sin(t)+( \sqrt(2)-2a-a+\frac{1-a}{\tan(t)}-\frac{5a}{\sin(t)})\cos(t)=a$
由此得出上面的最大上限

dlpg070

uk702 发表于 2020-12-9 21:03
n=26 时，不知这种情况下大伙是否计算过能否提供 a > 0.207317958160075956638385951... 的边长，从图上来 ...

利用mathe 139#的计算结果画图,验证
t=0.73793551389460718773965984811536761268;
a =0.20721104897365918253946967525090920670;
是第2优的解
画出了3个破坏的正方形,供参考
从图形看最上面斜放的正方形还可以提高一行,a可稍有有提高,大于0.2072110489,但可能仍小于0.207317958

a26_138#

1. (*uk702 138# dlpg070修改*)
   
2. (*a262start，尝试放 26 个*)
   
3. Clear["Global`*"];
   
4. t=0.73793551389460718773965984811536761268;
   
5. a =0.20721104897365918253946967525090920670;
   
6. n=26;u=4;v=6;d=3;f=5;
   
7. sub=0;
   
8. b=1-u a;
   
9. c=Sqrt[2]-v a;
   
10. td=t*180/Pi;
    
11. Print["n= ",n," \na= ",a,"\nb= ",b,"\nc= ",c,"\nt= ",t,"\ntd= ",td];
    
12. 
    
13. am=
    
14. (Sin[t] +Sqrt[2] Cos[t]+Cos[t]/Tan[t])/(4  Sin[t]+3  Cos[t] + Cos[t]/Tan[t]+5 Cos[t]/Sin[t]+ 1 )
    
15. xt=b Sin[t];yt=b Cos[t];(* 公式*)
    
16. xs=c Cos[t];ys=c Sin[t]; (* 公式*)
    
17. (* a=b Sin[t]+ c Cos[t]*) (* a *);
    
18. pBt={a+xt Sin[t],a-xt Cos[t]};
    
19. pAt=pBt+{-a  Sin[t],a Cos[t]};
    
20. pCt=pBt+{a Cos[t],a Sin[t]};
    
21. pDt=pCt+{-a  Sin[t],a Cos[t]};
    
22. 
    
23. Print[" xt= ",xt,"\nn= ",n," \na= ",a," \nt= ",t,"\npAt= ",N[pAt,30],"\npBt= ",N[pBt,30],"\nPCt= ",N[pCt,30],"\npDt= ",N[pDt,30]];
    
24. 
    
25. a262:=Module[{$MinPrecision=50,$MaxPrecision=50,w,h,f,esp,sqs,ra,rb,r1,r2,r3,r4,r5},w=1;h=N[Sqrt[2],20];(*注意h的写法,确保精度*)
    
26. Print["h= ",h];
    
27. fr=Rectangle[{0,0},{1,h}];
    
28. (*a=0.211520823989986052222250797555493157307027099075156414441346;*)(*a=0.207317958160075956638385951290;*)
    
29. esp=10.0^-10;
    
30. total=0.0;
    
31. (*各个矩形*)sqs={};intersections={};
    
32. (*底下第一排*)sqs=Append[sqs,Rectangle[{0,0},{a,a}]];
    
33. sqs=Append[sqs,Rectangle[{1-3*a,0},{1-2*a,a}]];
    
34. sqs=Append[sqs,Rectangle[{1-2*a,0},{1-a,a}]];
    
35. sqs=Append[sqs,Rectangle[{1-a,0},{1,a}]];
    
36. (*底下第二排*)sqs=Append[sqs,Rectangle[{0,h-5*a},{a,h-4*a}]];
    
37. (*sqs=Append[sqs,Rectangle[{a,a},{2*a,2*a}]];*)sqs=Append[sqs,Rectangle[{1-2*a,a},{1-a,2*a}]];
    
38. sqs=Append[sqs,Rectangle[{1-a,a},{1,2*a}]];
    
39. (*底下第三排*)sqs=Append[sqs,Rectangle[{0,h-4*a},{a,h-3*a}]];
    
40. sqs=Append[sqs,Rectangle[{a,h-4*a},{2*a,h-3*a}]];
    
41. sqs=Append[sqs,Rectangle[{1-a,2*a},{1,3*a}]];
    
42. (*第四排*)sqs=Append[sqs,Rectangle[{0,h-3*a},{a,h-2*a}]];
    
43. sqs=Append[sqs,Rectangle[{a,h-3*a},{2*a,h-2*a}]];
    
44. sqs=Append[sqs,Rectangle[{2*a,h-3*a},{3*a,h-2*a}]];
    
45. (*sqs=Append[sqs,Rectangle[{1-a,h-3*a},{1,h-2*a}]];*)(*第五排*)sqs=Append[sqs,Rectangle[{0,h-2*a},{a,h-a}]];
    
46. sqs=Append[sqs,Rectangle[{a,h-2*a},{2*a,h-a}]];
    
47. sqs=Append[sqs,Rectangle[{2*a,h-2*a},{3*a,h-a}]];
    
48. sqs=Append[sqs,Rectangle[{3*a,h-2*a},{4*a,h-a}]];
    
49. (*第六排*)sqs=Append[sqs,Rectangle[{0,h-a},{a,h}]];
    
50. sqs=Append[sqs,Rectangle[{a,h-a},{2*a,h}]];
    
51. sqs=Append[sqs,Rectangle[{2*a,h-a},{3*a,h}]];
    
52. sqs=Append[sqs,Rectangle[{3*a,h-a},{4*a,h}]];
    
53. sqsd={};(*破坏的正方形 sqsd *)
    
54. 
    
55. pgnd=Polygon[{
    
56. {1 a, (1+0)a+c},
    
57. {(1+1) a, (1+0) a+c},
    
58. {(1+1) a, (1+1) a+c},
    
59. {1 a,(1+1) a+c}
    
60. }];
    
61. AppendTo[sqsd,pgnd];
    
62. pgnd=Polygon[{
    
63. {2 a, (2+0)a+c},
    
64. {(2+1) a, (2+0) a+c},
    
65. {(2+1) a, (2+1) a+c},
    
66. {2 a,(2+1) a+c}
    
67. }];
    
68. AppendTo[sqsd,pgnd];
    
69. pgnd=Polygon[{
    
70. {3 a, (3+0)a+c},
    
71. {(3+1) a, (3+0) a+c},
    
72. {(3+1) a, (3+1) a+c},
    
73. {3 a,(3+1) a+c}
    
74. }];
    
75. AppendTo[sqsd,pgnd];
    
76. 
    
77. 
    
78. b=1-4 a;
    
79. c=Sqrt[2]-6 a;
    
80. M={1,a-c Tan[t] (1-a) + (5 a)/Sin[t] -3.62a};
    
81. M={1,a-b Tan[t] (1-a) + (5 a)/Sin[t] -3.62a};(* c?b? 3.62? *)
    
82. Nn={4a,Sqrt[2]-2 a};
    
83. G={2*a,h-4*a};H={1-2*a,2*a};
    
84. (*过 w1 作 GH 的平行线 l1，过 G 点作 l1 的垂线 l2*)w1={(2*a+1-a)/2,(h-3*a+2*a)/2};
    
85. p1=w1+a*(G-H)/2/EuclideanDistance[G,H];
    
86. p2=w1-a*(G-H)/2/EuclideanDistance[G,H];
    
87. v=RotationTransform[90 Degree,{0,0}][p2-p1];
    
88. v=(M-pCt)/4;
    
89. Print["v=",v];
    
90. p3=p1+v;
    
91. p4=p2+v;
    
92. r0=Polygon[{p1,p3,p4,p2}];
    
93. (*r1=TransformedRegion[r0,TranslationTransform[{0.023,0.039}]];*)
    
94. 
    
95. r1=Polygon[{pAt,pBt,pCt,pDt}];(*暂时手工写一个*)
    
96. r2=Polygon[{pAt+v,pBt+v,pCt+v,pDt+v} ];
    
97. r3=Polygon[{pAt+2v,pBt+2 v,pCt+2 v,pDt+2 v}];
    
98. r4=Polygon[{pAt+3v,pBt+3v,pCt+3v,pDt+3v}];
    
99. r5=Polygon[{pAt+4v,pBt+4v,pCt+4v,pDt+4v}];
    
100. (*
     
101. r2=TransformedRegion[r1,TranslationTransform[v]];
     
102. r3=TransformedRegion[r1,TranslationTransform[-v]];
     
103. r4=TransformedRegion[r1,TranslationTransform[-2*v]];
     
104. r5=TransformedRegion[r1,TranslationTransform[-3*v]];
     
105. *)
     
106. (*语句后面不能加;，否则相当于静默不显示图形*)Graphics[{EdgeForm[{Thin,RGBColor["#807F7D"]}],White,fr,Opacity[0.7],EdgeForm[{Thin,RGBColor["#a099FF"]}],RGBColor["#FBE0E0"],sqs,r1,r2,r3,r4,r5,
     
107. LightGray,sqsd,
     
108. (*Yellow,r0,*)
     
109. (*Blue,rt,*)
     
110. Text[Style["M",Black,FontSize->10],M+{0.03,0}],
     
111. Text[Style["N",Black,FontSize->10],Nn+{0.03,0}],
     
112. Text[Style["G",Black,FontSize->10],G+{0.03,0}],
     
113. Text[Style["H",Black,FontSize->10],H+{0.03,0}],
     
114. Text[Style["p1",Black,FontSize->10],p1+{0.03,0}],
     
115. Text[Style["p2",Black,FontSize->10],p2+{0.03,0}],
     
116. Red,PointSize[0.03],Point[{w1}]}
     
117. ,PlotLabel->Style[Framed["A4_uk702138"<>ToString[n]<>"_"<>ToString[sub]<>"a"<>ToString[N[a,8]]],10,Blue,Background-> RGBColor["#FBE0E0"]]]];a262
     
118. 
     
119. (*a262end*)

复制代码