均分田地，田埂最短问题

mathe

正方形8个区域找到更优的结果（更加对称）
3.59784289205435

mathe

正方形n=9的情况及其复杂，比如下图
可以达到3.92165555240105，比前面全对称的132#要更好

hujunhua

@mathe 这样的高度对称呢？

mathe

这个应该8段15度圆弧和四段30度圆弧，可以笔算

mathe

152#的坐标数据
t9.out (1.43 KB, 下载次数: 3)

2019-7-14 09:57 上传

点击文件名下载附件

t9.xml (2.97 KB, 下载次数: 3)

2019-7-14 09:57 上传

点击文件名下载附件

mathe

总长3.92057823229837
A(0.35569896136317,0.29386488366869)
C(0.62864342054998,0.37135657945002)
G(0.69263914223257,0.30736085776743)
I(0.32143659208730,0.00000000000000)
K(0.65217431764688,0.00000000000000)
                A=>C(-0.01483148068210)
                A=>B(-0.02966296136420)
                A=>I(0.11606821321747)
                K=>G(-0.13089969389957)

数学星空

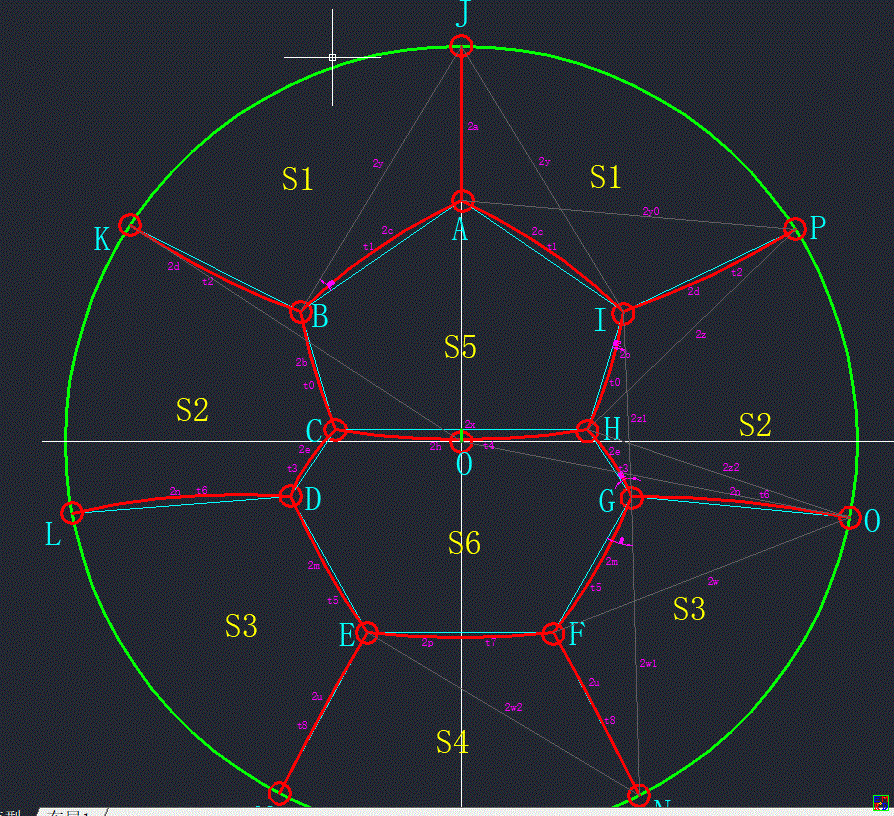
下面我仿照mathe 比较简单易懂的坐标解析法来计算各个未知量：



[1, A, 0, 1 - 2*a],
[2, B, -x1, y1],
[3, I, x1, y1],
[4, C, -x2, 2*x],
[5, H, x2, 2*x],
[6, J, 0, 1],
[7, K, -x11, y11],
[8, P, x11, y11],
[9, D, -x3, y3],
[10, G, x3, y3],
[11, L, -x12, y12],
[12, O, x12, y12],
[13, E, -p, y4],
[14, F, p, y4],
[15, M, -x13, y13],
[16, N, x13, y13]]

下面包含5个面积（S1,S3,S4,S5,S6)，3个(P,O,N)与圆周正交，3个(P,O,N)在圆周上,4个(I,H,G,F)交点倒数和为0，8个角度(A,I,H,G,F点）约束，9个（t0,t1,t2,t3..,t8)弧度，7条边（边界,AJ=2a,AI=2c,IP=2d,IH=2b,HG=2e,GO=2n,GF=2m,CH=2h,FE=2p,FN=2u），8条辅助边(JI=2y,AP=2y0,PH=2z,IG=2z1,HO=2z2,OF=2w,GN=2w1,EN=2w2)

共列了40条方程

{4*b^2 - (x1 - x2)^2 - (y1 - 2*x)^2, 4*c^2 - x1^2 - (1 - 2*a - y1)^2, 4*d^2 - (x1 - x11)^2 - (y1 - y11)^2, 4*e^2 - (x2 - x3)^2 - (2*x - y3)^2, 4*m^2 - (x3 - p)^2 - (y3 - y4)^2, 4*n^2 - (x3 - x12)^2 - (y3 - y12)^2, 4*u^2 - (p - x13)^2 - (y4 - y13)^2, 4*w^2 - (p - x12)^2 - (y4 - y12)^2, 4*w1^2 - (x3 - x13)^2 - (y3 - y13)^2, 4*w2^2 - (-p - x13)^2 - (y4 - y13)^2, 4*y^2 - x1^2 - (1 - y1)^2, 4*y0^2 - x11^2 - (1 - 2*a - y11)^2, 4*z^2 - (x11 - x2)^2 - (y11 - 2*x)^2, 4*z1^2 - (x1 - x3)^2 - (y1 - y3)^2, 4*z2^2 - (x2 - x12)^2 - (2*x - y12)^2, -sin(t0)/b + sin(t1)/c + sin(t2)/d, -sin(t0)/b + sin(t4)/h + sin(t3)/e, -sin(t3)/e + sin(t5)/m + sin(t6)/n, -sin(t5)/m + sin(t7)/p + sin(t8)/u, 2*t0 + 2*t1 + t4 - Pi/6, 2*t5 + 2*t3 + t7 - t4, a^2 + c^2 + 2*a*c*sin(Pi/6 + t1) - y^2, b^2 + e^2 + 2*b*e*sin(Pi/6 + t0 + t3) - z1^2, d^2 + b^2 + 2*d*b*sin(Pi/6 + t2 + t0) - z^2, d^2 + c^2 + 2*d*c*sin(Pi/6 + t1 - t2) - y0^2, e^2 + n^2 + 2*e*n*sin(Pi/6 + t3 + t6) - z2^2, m^2 + u^2 + 2*m*u*sin(Pi/6 + t5 + t8) - w1^2, n^2 + m^2 + 2*n*m*sin(Pi/6 - t6 + t5) - w^2, p^2 + u^2 + 2*p*u*sin(Pi/6 + t7 - t8) - w2^2, p^2 + y4^2 - 1 - 4*u^2 + 4*u*cos(t8), x1^2 + y1^2 - 1 - 4*d^2 + 4*d*cos(t2), x3^2 + y3^2 - 1 - 4*n^2 + 4*n*cos(t6), c^2*(2*t1 - sin(2*t1))/sin(t1)^2 + b^2*(2*t0 - sin(2*t0))/sin(t0)^2 + h^2*(2*t4 - sin(2*t4))/(2*sin(t4)^2) - Pi/9 + x1*(1 - 2*a) - 2*x1*x + x2*y1 - 2*x2*x, -c^2*(2*t1 - sin(2*t1))/(2*sin(t1)^2) + d^2*(2*t2 - sin(2*t2))/(2*sin(t2)^2) + Pi/18 + t1 - t2 - sin(Pi/3 + 2*t1 - 2*t2)/2 - x1*(1 - 2*a)/2 + x1*y11/2 - x11*y1/2 + x11/2, -p^2*(2*t7 - sin(2*t7))/(2*sin(t7)^2) + u^2*(2*t8 - sin(2*t8))/sin(t8)^2 + Pi/18 + t7 - 2*t8 - sin(Pi/3 + 2*t7 - 4*t8)/2 - p*y13 + p*y4 - x13*y13 + x13*y4, -h^2*(2*t4 - sin(2*t4))/(2*sin(t4)^2) + e^2*(2*t3 - sin(2*t3))/sin(t3)^2 + m^2*(2*t5 - sin(2*t5))/sin(t5)^2 + p^2*(2*t7 - sin(2*t7))/(2*sin(t7)^2) - Pi/9 + p*y3 - p*y4 + 2*x2*x + 2*x3*x - x2*y3 - x3*y4, -m^2*(2*t5 - sin(2*t5))/(2*sin(t5)^2) + n^2*(2*t6 - sin(2*t6))/(2*sin(t6)^2) - u^2*(2*t8 - sin(2*t8))/(2*sin(t8)^2) + Pi/18 + t5 - t6 + t8 - sin(Pi/3 + 2*t5 - 2*t6 + 2*t8)/2 + x12*y3/2 - x3*y12/2 + x3*y4/2 - p*y3/2 + p*y13/2 - x13*y4/2 + x13*y12/2 - x12*y13/2, x11^2 + y11^2 - 1, x12^2 + y12^2 - 1, x13^2 + y13^2 - 1}

根据mathe 得到的数据可以计算出40个未知数为

{a = 0.195525067449090, b = 0.155084180733908, c = 0.247935926033849, d = 0.242058598199665, e = 0.1013196777756024341605942, h = 0.318181449956655, m = 0.198011951897411, n = 0.276873796158457, p = 0.235075742493475, t0 = 0.12260582929224, t1 = 0.08407578100475, t2 = 0.10911694634697, t3 = 0.04488378327096, t4 = 0.11023555500427, t5 = 0.01365160332952, t6 = 0.10370943688338, t7 = -0.00683521819668, t8 = 0.02264572630074, u = 0.231017541128632, w = 0.4024049907579719038653181, w1 = 0.3757222319230400163881143, w2 = 0.4001750883196611431218536, x = 0.01433863302, x1 = 0.4070998671345, x11 = 0.83990883262215, x12 = 0.98257552176460, x13 = 0.45419827613861, x2 = 0.31818144995666, x3 = 0.4307453188549, y = 0.3937764655711446600034546, y0 = 0.4212577142004209990240206, y1 = 0.325826937997, y11 = 0.54272751255423, y12 = -0.18586377815225, y13 = -0.890900626306, y3 = -0.1398222408899, y4 = -0.4841307497353, z = 0.3662127516077764007003215, z1 = 0.2331245724851026872311345, z2 = 0.3490871461033169616953729}

将40个未知数代入方程得到：

[-6.1693257*10^(-13), -1.857645632*10^(-13), -3.76752057*10^(-12), 3.4162359*10^(-13), 1.599149845*10^(-12), 3.1549837*10^(-13), -1.0738983*10^(-14), 2.801252*10^(-14), -2.79803387*10^(-13), -1.98842891*10^(-13), -1.935338640*10^(-12), 1.248042769*10^(-12), -6.18450427*10^(-14), 8.801171*10^(-14), 7.087788*10^(-14), -2.05484*10^(-16), 5.*10^(-21), -4.*10^(-21), 1.0627977*10^(-14), -6.*10^(-21), -7.*10^(-21), -4.05607*10^(-16), -3.*10^(-21), 5.100746*10^(-14), 1.2809282*10^(-13), -1.313129*10^(-14), -7.294349*10^(-15), 1.6820592*10^(-13), -6.619734*10^(-14), -4.996257*10^(-14), 2.550558577*10^(-12), -2.8316352534*10^(-12), -4.887308*10^(-14), 1.*10^(-14), 4.66630*10^(-15), 4.73272*10^(-15), -2.9191870*10^(-13), -2.7705928*10^(-13), -3.66915*10^(-14), -7.286848*10^(-14)]

可以认为方程是准确的！

本以为将mathe的数据作为初始值应该很容易算出更精确的未知数，但是maple 并没有算出结果，直接罢工了！！

谁有兴趣可以计算一下方程，得到更精确的解

mathe

12个区域的一个结果，已经可以看出蜂窝化趋势了

Result:
        A(-0.15729185154765,-0.55055810437779)
                A=>P(-0.11748225497812)
                A=>B(-0.00162828614664)
                A=>F(0.05480041062509)
        B(-0.54503605526997,-0.34876182444602)
                B=>A(0.00162828614664)
                B=>O(0.00138566375857)
                B=>D(-0.00330936029454)
        C(-0.47495891164496,0.13433922379828)
                C=>D(0.02897705588438)
                C=>E(-0.21855283629943)
                C=>G(0.09656571325125)
        D(-0.56181301907799,0.08343702269333)
                D=>V(0.12298004145325)
                D=>C(-0.02897705588438)
                D=>B(0.00330936029454)
        E(-0.37037646858140,0.55982389069326)
                E=>C(0.21855283629943)
                E=>U(-0.00126264438481)
                E=>M(-0.17664687463703)
        F(0.00458463337158,-0.43407085993083)
                F=>A(-0.05480041062509)
                F=>G(0.00785060030059)
                F=>K(0.07699863352223)
        G(-0.05554987547701,-0.06799899053971)
                G=>F(-0.00785060030059)
                G=>C(-0.09656571325125)
                G=>L(0.04795516778196)
        H(0.57241765617468,-0.20008521608281)
                H=>I(0.05355350721972)
                H=>R(-0.06573357290645)
                H=>K(-0.02631989270494)
        I(0.47785417921699,0.01445415974246)
                I=>H(-0.05355350721972)
                I=>J(0.16118646115829)
                I=>L(-0.10106626536433)
        J(0.61017742880337,0.31292287011501)
                J=>S(0.08388794524678)
                J=>I(-0.16118646115829)
                J=>N(0.12719488408066)
        K(0.29523370179664,-0.52132209444828)
                K=>H(0.02631989270494)
                K=>Q(0.07721322967570)
                K=>F(-0.07699863352223)
        L(0.09925421022508,0.07398250353715)
                L=>I(0.10106626536433)
                L=>G(-0.04795516778196)
                L=>M(-0.01612181637137)
        M(-0.01474726219187,0.51960309105863)
                M=>L(0.01612181637137)
                M=>E(0.17664687463703)
                M=>N(-0.11802934862364)
        N(0.16481201524201,0.65326557644273)
                N=>M(0.11802934862364)
                N=>T(-0.09866827159306)
                N=>J(-0.12719488408066)
        O(-0.84272149153288,-0.53834978193420)
                O=>B(-0.00138566375857)
        P(-0.18846643169914,-0.98207963227153)
                P=>A(0.11748225497812)
        Q(0.44698200314889,-0.89454294970169)
                Q=>K(-0.07721322967570)
        R(0.95724761945335,-0.28926976172924)
                R=>H(0.06573357290645)
        S(0.90676083482026,0.42164533489186)
                S=>J(-0.08388794524678)
        T(0.19775029962801,0.98025242616228)
                T=>N(0.09866827159306)
        U(-0.55228386384883,0.83365612438955)
                U=>E(0.00126264438481)
        V(-0.97082470902040,0.23979029245460)
                V=>D(-0.12298004145325)
Total arc len 8.93799761323269

zeroieme

又爬一次楼，没看见mathe的编程细节。从各段发言揣测他的程序是先给结构后定位。望@mathe指正。

我想了个“紧箍咒”算法：N个分离面积为1的圆“泡泡”，外围边界从不接触逐渐缩小直到面积等于N。内部泡泡挤压成的形状就是结果。

mathe

从结果上看,正方形要远远比圆形复杂。比如四个区域，圆形的只找出两种情况，都已经被论坛中网友找到了，
但是正方形可以找到下面6中不同的情况（只是优秀的很少），比较有意思的是其中排名第二的竟然是不对称的。

而5个区域情况圆形同样只有两种，大家也都找到了，但是正方形的可以找到21种
而圆形的6个区域才找到四种

下面附件是结果数据
eqad.tgz (15.94 KB, 下载次数: 2)

2019-7-17 13:03 上传

点击文件名下载附件