均分田地，田埂最短问题

gxqcn

mathe 发表于 2019-6-20 14:09
正方形分成7个区域先猜测一个对称的图

总长度3.28072646427294

mathe 的 116# 中的第一幅图，中间似乎已出现“等角六边形”（我很兴奋），但左右“两肋”却是两段圆弧而非直线段（又很遗憾），

如果内部交界点处切线夹角必须满足两两成120°的规律，那么，这“两肋”之间应该的连线应该是已退化为线段（因为两端的切线正好重合了）。
究竟是那里出了问题？

数学星空

关于112#及115#的计算过程及结果：

即关于\(N=8\) 构型I的计算：



设\(AA1=2a,AB=2b,BE=2c,BF=2d\),三段圆弧\(\widehat{AB},\widehat{BE},\widehat{BF}\)的半径,半弧长,圆周角分别为\(R_0,R_1,R_2,t_0,t_1,t_2,\theta_0,\theta_1,\theta_2\)则有下列方程：

对曲边三边形BEF有面积方程：

\(\frac{1}{2}(\frac{c}{\sin(t_1)})^2(2t_1-\sin(2t_1))+\frac{1}{2}(\frac{d}{\sin(t_2)})^2(2t_2-\sin(2t_2))+2cd\sin(\frac{2\pi}{3}-t_1-t_2)+\frac{1}{2}(\frac{2\pi}{3}-2t_1-2t_2-\sin(\frac{2\pi}{3}-2t_1-t_2))=\frac{\pi}{8}\)

对曲边五边形ABFF2B2有面积方程：

\((\frac{b}{\sin(t_0)})^2(2t_0-\sin(2t_0))+2b^2\sin(\frac{2\pi}{3}-2t_0)+4(2b\cos(\frac{\pi}{6}+t_0)+d\cos(\frac{\pi}{2}+2t_0-t_2))d\sin(\frac{\pi}{2}+2t_0-t_2)+\frac{1}{2}(4t_2-4t_0-\sin(4t_2-4t_0))-\frac{d}{\sin(t_2)})^2(2t_2-\sin(2t_2))=\frac{\pi}{8}\)

对曲边五边形ABEE1B1有面积方程：

\(4(a+b\cos(\frac{\pi}{3}-t_0))b\sin(\frac{\pi}{3}-t_0)+2(2a+4b\cos(\frac{\pi}{3}-t_0))c\sin(\frac{\pi}{3}+t_1+2t_0)-2c^2\sin(\frac{2\pi}{3}+2t_1+4t_0)-(\frac{c}{\sin(t_1)})^2(2t_1-\sin(2t_1))+(\frac{b}{\sin(t_0)})^2(2t_0-\sin(2t_0))+\frac{1}{2}(-\frac{\pi}{3}+4t_1+4t_0-\sin(-\frac{\pi}{3}+4t_1+4t_0))=\frac{\pi}{8}\)

分别在三角形OEB,ABO计算OB有：

\(1+4c^2-4c\cos(t_1)=a^2+4b^2-4ab\cos(\frac{2\pi}{3}+t_0)\)

分别对三角形OBF,OAB计算OB:

\(1+4d^2-4d\cos(t_2)=a^2+4b^2-4ab\cos(\frac{2\pi}{3}+t_0)\)

在五边形ABEE1B1中计算EE1/2:

\(\sin(2t_0+2t_1-\frac{\pi}{6})=(a+2b\cos(\frac{\pi}{3}-t_0))-2c\cos(\frac{\pi}{3}+2t_0+t_1)\)

对B点三段圆弧的半径倒数和为0:

\(\frac{\sin(t_0)}{b}-\frac{\sin(t_1)}{c}+\frac{\sin(t_2)}{d}=0\)

求解以上方程得到：

\(a =0 .1404073125854350146716747, b = 0.1373435153588433544790543, c =0 .3784271511063521270499447, d = 0.3338495743821102038744899, t_0 = 0.03407923799948390366169432, t_1 =0 .3200553392647668414219998, t_2 =0 .1959876619928881608748679\)

\(R_0 = 4.030903037304680237279858, R_1 = 1.202810519083707801365736, R_2 = 1.714375517575520524011609\)

\(L=2a+8R_0t_0+8R_1t_1+8R_2t_2=7.147474482652381763627598\)

数学星空

关于下列构型有着很强的规律性，但不知是否最优（似乎与正多面体构型类似，中间叠放部分只存在三边形，五边形，六边形的基本单元？）？








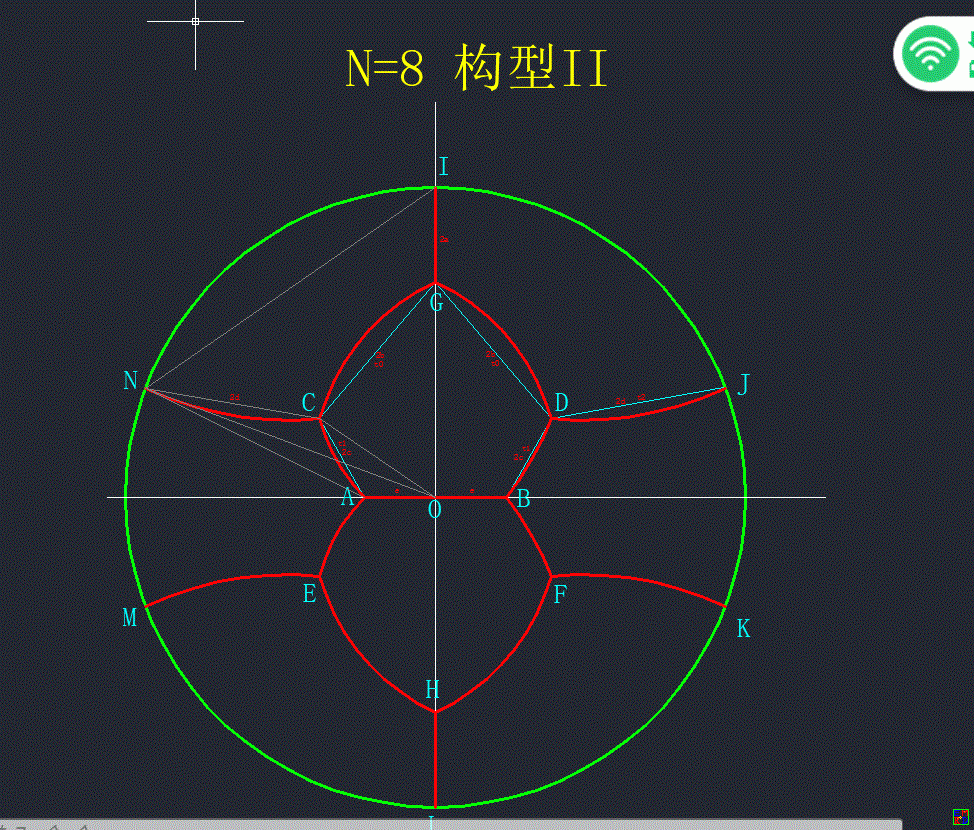
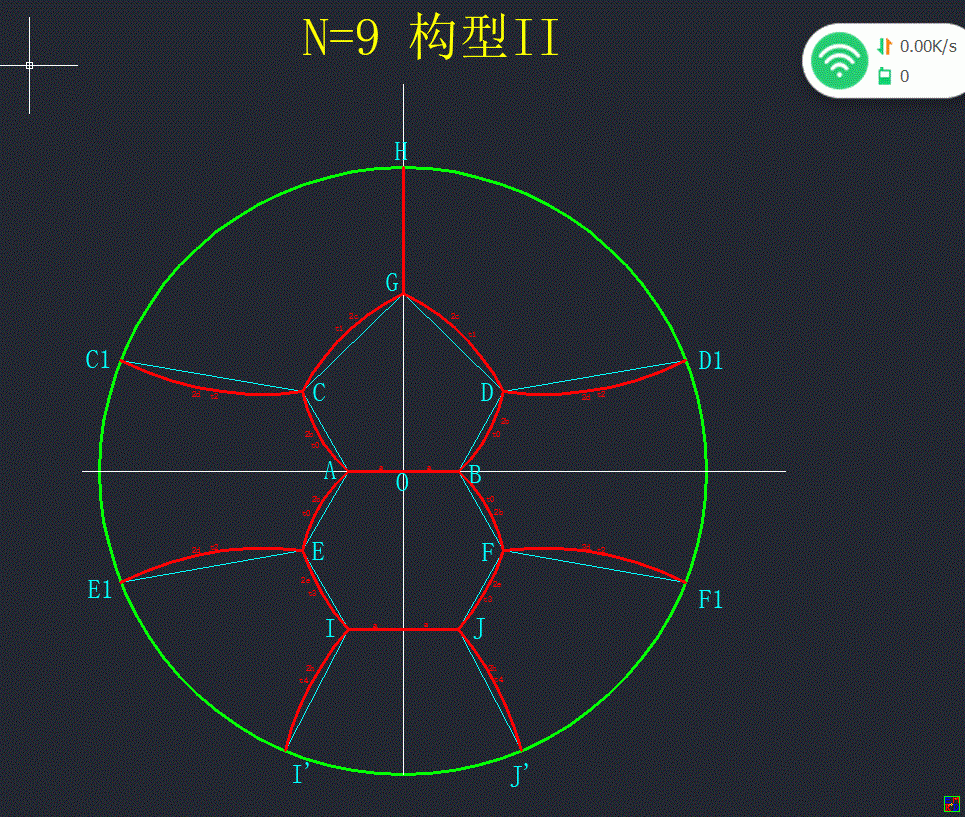
对于\(N=8\) 构型II 的计算：

设\(IG=2a,CG=2b,CA=2c,AO=BO=e,NC=2d\),三段圆弧\(\widehat{CG},\widehat{CA},\widehat{CN}\)的半径,半弧长,圆周角分别为\(R_0,R_1,R_2,t_0,t_1,t_2,\theta_0,\theta_1,\theta_2\)则有下列方程：

对曲边五边形ABDGC有面积方程：

\((\frac{c}{\sin(t_1)})^2(2t_1-\sin(2t_1))+(\frac{b}{\sin(t_0)})^2(2t_0-\sin(2t_0))+2b^2\sin(\frac{2\pi}{3}-2t_0)+4(e+c\cos(\frac{\pi}{3}+t_1)c\sin(\frac{\pi}{3}+t_1)=\frac{\pi}{8}\)

对曲边五边形CAEMN有面积方程：

\(-(\frac{c}{\sin(t_1)})^2(2t_1-\sin(2t_1))+2c^2\sin(\frac{2\pi}{3}+2t_1)+4(2c\sin(\frac{\pi}{3}+t_1)+d\cos(\frac{\pi}{2}-2t_1-t_2))d\sin(\frac{\pi}{2}-2t_1-t_2)+\frac{1}{2}(4t_1+4t_2-\sin(4t_1+4t_2))=\frac{\pi}{8}\)


对\(\angle GDB \)有：

\(\frac{\pi}{2}+t_0+t_1=\frac{2\pi}{3}-t_0-t_1\)

对单位圆半径IO=IG+GO有方程：

\(2a+2b\sin(\frac{\pi}{6}+t_0))+2c\sin(\frac{\pi}{2}-2t_0-t_1)=1\)

分别对三角形ANO,CNO计算NO:

\(1+e^2-2e\cos(2t_1+2t_2)=4c^2+4d^2-8cd\cos(\frac{2\pi}{3}+t_1+t_2)\)

分别对三角形ACG,AGO计算AG:

\(4b^2+4c^2-8bc\cos(\frac{2\pi}{3}-t_0-t_1)=e^2+(1-2a)^2\)

对C点三段圆弧的半径倒数和为0:

\(\frac{\sin(t_0)}{b}-\frac{\sin(t_1)}{c}+\frac{\sin(t_2)}{d}=0\)

分别对五边形OCNME,三角形NOM计算MN边上的高线:

\(e+2c\cos(\frac{\pi}{3}+t_1)+2d\sin(\frac{\pi}{2}-2t_1-t_2)=\cos(2t_1+2t_2)\)

可以计算出:

\(a =0 .1901769795817331618309615, b =0 .2884422119188707996520303, c =0 .1443490260954234766393950, d = 0.2381022966476015149264157, e = 0.3440802749179558466096139\)

\(t_0 =0 .1359304941570299131125923, t_1 =0 .1258688936421195234259614, t_2 = 0.09535393230790106642941993\)

\(R_0 = 2.128531900121159210220004, R_1 = 1.149854270368826336282691, R_2 = 2.500825011796743735790923\)

\(L=4a+2e+8R_0t_0+8R_1t_1+8R_2t_2=6.829082682260719120355591\)

画图得到：

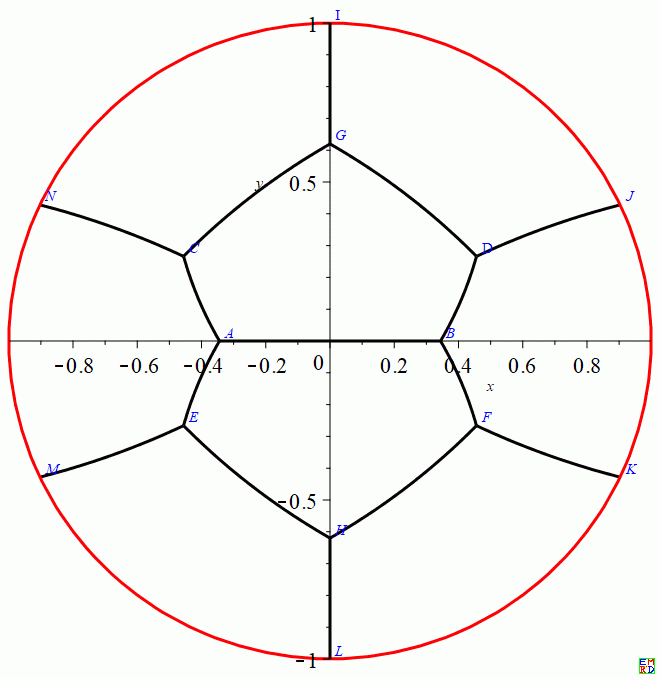
mathe

N=8还存在另外一种可能的构图

相当于选择N=7的最优构图，将6条散射线中一条的尾端产生两个分叉，就可以多处一个区域。然后调整各点的位置和分界线的弧度来达到平衡。甚至我们还可以试验N=7也有类似的方案。而N=8也可以试验从N=6最优图的五条散射线中两条的尾端各自产生分叉，多出两个区域。
我觉得这种方案比中间两个区域挤在一起应该靠谱些

zeroieme

一般情况，完全计算所有边长的图形，接近圆形的面积较大；有一段不必纳入边长和的图形，接近半圆的面积较大。所以把边缘区域“拉得过长”的方案，不如靠边界的两边“粘合”起来。“缩入”成为内部区域。问题是那个“长宽比”该是多少？

zeroieme

还是无法传图

N=9  构型 3
内部三个相接五边形，中间相接是三段等长、之间为120°的线段。每个内部五边形除了中间相接部分，另外的三段为曲线，非中间相接的两顶点与边界圆各有一线段/弧线连接。

mathe

划分成8个区域的近似逼近解，中心“七边形”的方案还是有差距的。
6.92792495028745：

7.07740541540335：

6.91427988771841：

mathe

前面代码显然计算精度不够，得到的结果不好，
现在修订了代码，结果要好很多:
6.82326123654612

c8.xml (2.52 KB, 下载次数: 9)

2019-6-29 17:04 上传

点击文件名下载附件

（具体数据）
7.04017022768063（计算这个图程序停不下来，应该是结果无法收敛，中间部分应该需要改成七边形，转为了星空的最优解）

6.76815953042611

c8.3.xml (2.46 KB, 下载次数: 9)

2019-6-29 17:05 上传

点击文件名下载附件

（具体数据）

mathe

终于在n=9时找到了超越星空104#的解的方案
7.31494334143164：

        A(0.60709203264349,-0.04753106466644)
                A=>J(-0.00000000000004)
                A=>B(0.08407578100477)
                A=>I(-0.08407578100476)
        B(0.35660871384379,0.38042570964165)
                B=>K(-0.10911694634698)
                B=>A(-0.08407578100477)
                B=>C(0.12260582929224)
        C(0.05342515808133,0.31497233714764)
                C=>B(-0.12260582929224)
                C=>H(0.11023555500428)
                C=>D(0.04488378327095)
        D(-0.10577420000672,0.44034487322536)
                D=>L(0.10370943688338)
                D=>C(-0.04488378327095)
                D=>E(0.01365160332953)
        E(-0.46430508783646,0.27214696940693)
                E=>M(0.02264572630075)
                E=>D(-0.01365160332953)
                E=>F(-0.00683521819668)
        F(-0.50100236279553,-0.19657014020826)
                F=>G(0.01365160332953)
                F=>N(-0.02264572630075)
                F=>E(0.00683521819668)
        G(-0.17301712024887,-0.41851746064377)
                G=>O(-0.10370943688338)
                G=>F(-0.01365160332953)
                G=>H(0.04488378327095)
        H(0.00375439225886,-0.31944909645048)
                H=>C(-0.11023555500428)
                H=>I(0.12260582929225)
                H=>G(-0.04488378327095)
        I(0.29305704491544,-0.43128999961873)
                I=>H(-0.12260582929225)
                I=>A(0.08407578100476)
                I=>P(0.10911694634698)
        J(0.99694912083112,-0.07805415090862)
                J=>A(0.00000000000004)
        K(0.60663008726281,0.79498423709374)
                K=>B(0.10911694634698)
        L(-0.10860263216838,0.99408524196172)
                L=>D(-0.10370943688338)
        M(-0.85273053535571,0.52235106400961)
                M=>E(-0.02264572630075)
        N(-0.92363465693199,-0.38327408014909)
                N=>F(0.02264572630075)
        O(-0.26199082827818,-0.96507036318505)
                O=>G(0.10370943688338)
        P(0.47551334572094,-0.87970850742805)
                P=>I(-0.10911694634698)

mathe

另外圆形情况在n充分大时，所有区域都近似边长为a的六边形，可以得出田埂总长近似$3sqrt{{2pi n}/{3sqrt{3}}}-pi$，这个数值可以用来作为一个参考值。
于是如果一个n个区域的划分方案达到了长度$L_n$,那么我们可以把${3sqrt{{2pi n}/{3sqrt{3}}}-pi}/{L_n}$定义为这种方案的有效率
于是现在已知的最佳有效率为

n	l	ratio	where	who
1	0	-	-	-
2	2	76.2%	-	-
3	3	85.7%	42#	KeyTo9_Fans
4	3.945702967	87.6%	84#	mathe
5	4.833846644	87.6%	87#	mathe
6	5.40679693	91.3%	99#	mathe
7	6	93.1%	95# 具体数据参考 数学星空的104#	zgg__
8	6.647231018	93.1%	104#	数学星空
9	7.314943341	92.3%	129#	mathe
10	7.837055233	93.0%	150#	mathe
11	8.795638460	88.7%	104#	数学星空

同样对于正方形，有效率可以定义为${3sqrt{{2 n}/{3sqrt{3}}}-2}/{L_n}$，得出当前已知最佳有效率为

n	l	ratio	where	who
1	0	-	-	-
2	1	63.2%	-	-
3	1.623278144	75.4%	13#	KeyTo9_Fans
4	1.975592885	87.2%	13#	KeyTo9_Fans
5	2.502112930	86.4%	11#	KeyTo9_Fans
6	2.939946252	87.0%	114#	mathe
7	3.280726464	89.1%	116#	mathe
8	3.597842892	90.7%	116#	mathe