果树种植最优解精美图形作法探讨

sheng_jianguo

数学星空 发表于 2019-12-23 18:50
125# mathe的计算方法，我不太确定下面理解是否正确：

设变换前的四点坐标 \(Q=[Q_1,Q_2,Q_3],V=[V_1,V_ ...

一些问题mathe已解答了，我再补充说一点：
一般射影变换矩阵S定义中规定R9=1（因为S中每个元素乘上非零常数c后的矩阵S‘与S是相同的射影变换）故你的矩阵T中可将第9列删去，并将其中Ql3改为Q3+Ql3；Vl3改为V3+Vl3；Ul3改为U3+Ul3；Nl3改为N3+Nl3，这样就是12X12阶矩阵了，R中将R9删去。很容易求解出R（如果有非零解），而且解是唯一的（说明4点到4点的射影变换最多只有1个）。要注意的是：当射影变换前的点比如Q（见129#）在对应射影变换后的点SQ中如果Z坐标SQz不等于0，则X,Y,Z坐标都需除以SQz后的点就是我们绘图中的坐标点。

数学星空

经过反复选点，我们终于得到了想要的图形

以 \(X[0.3819660120, 0.500000000000000, 1.]->[0,\frac{\sqrt{3}}{3},1], S[-0.2360679760, 0.309016994000000, 1.]->[-\frac{1}{2},-\frac{\sqrt{3}}{6},1], V[1., 0., 0.]->[\frac{1}{2},-\frac{\sqrt{3}}{6},1], A[0., 1., 1.]->[0,0,1]\)

变换矩阵为

[[0.08333333354, 0.06366100223, -0.06366100220], [-0.04811252262, 0.06962909663, -0.06962909663], [0.1666666682, -1.688415862, 0.6884158608]]


变换后坐标为：

[-3.00000024462111*10^(-11), -0., A], [0.290089363324209, 0.0749007508253550, B], [-0.149627095024728, -0.101143946313708, C], [-0.322001791407985, 0.0196268111827693, D], [-0.0527864047990069, -0.288675134646237, E], [0.0230063539749857, -0.137696205052507, F], [-0.0760143113346731, 0.0196268108758734, G], [-0.118033990310333, -0.288675134832972, H], [0.322001787549834, 0.0196268103793053, I], [-0.140734608613517, -0.153928202899481, J], [-0.290089366594055, 0.0749007527258173, K], [0.0924746297462326, -0.101143945903521, L], [-0.159719142240100, -0.0412393049053934, M], [0.0760143107540551, 0.0196268106862013, N], [0.0815594803413376, -0.0210585672866196, O], [-0.196723315733394, -0.0681469552981864, P], [-0.0457902735671232, -0.173895062156239, Q], [-3.58411239631470*10^(-10), -0.183524788248270, R], [-0.500000002363119, -0.288675135926141, S], [-0.0924746302707499, -0.101143945970514, T], [-0.0377045748401054, -0.0412393049586264, U], [0.499999996640000, -0.288675133064189, V], [-1.48269315978281*10^(-10), -0.101143945937017, W], [6.57797711853677*10^(-11), 0.577350269402003, X]

画图得到：

数学星空

108#结果：

L[-1.4142135620, -1., 1.]->[-1,1,1],    P[1., -1.7071067810, 1.]->[-1,-1,1],     S[1., 0., 0.]->[-1,1,1],    N[1., -0.7071067810, 0.]->[1,1,1]

变换矩阵为

[[0.108703732692843, 0.371137758481040, 0.371137758481040], [-0.108703732692843, 0.0636771722903307, 0.0636771722903305], [0.108703732692842, 0.371137758481039, 0.678598344509521]]


变换后坐标：

[1.00000000000000, 0.171572875125784, A], [0.640754482104539, -8.12365007213324*10^(-11), B], [0.609475708311524, -0.333333333367677, C], [0.656854249567378, 0.171572875125784, D], [0.707106781263819, 0.707106780954737, E], [0.707106781218556, -0.707106781218556, F], [0.609475708311524, 0.0571909583208012, G], [0.783611624929784, -0.261203875014653, H], [0.522407750010499, -7.19991730239376*10^(-11), I], [0.783611624942137, 0.261203874828479, J], [0.609475708331641, 0.333333333195964, K], [-1.00000000000000, 0.999999999999999, L], [0.707106781263820, 0.121320343482372, M], [1.00000000000000, 1.00000000000000, N], [0.828427124783690, -9.05283505737452*10^(-11), O], [-1.00000000000000, -1.00000000000000, P], [0.609475708331642, -0.0571909584723970, Q], [0.656854249567378, -0.171572875306841, R], [1.00000000000000, -1.00000000000000, S], [0.546918160770481, 0.0938363213018966, T], [0.707106781218556, -0.121320343655663, U], [0.546918160716323, -0.0938363214326451, V], [1.00000000000000, -0.171572875381836, W], [5.41641632330548*10^(-16), -8.12462448495822*10^(-16), X]


画图得到：

数学星空

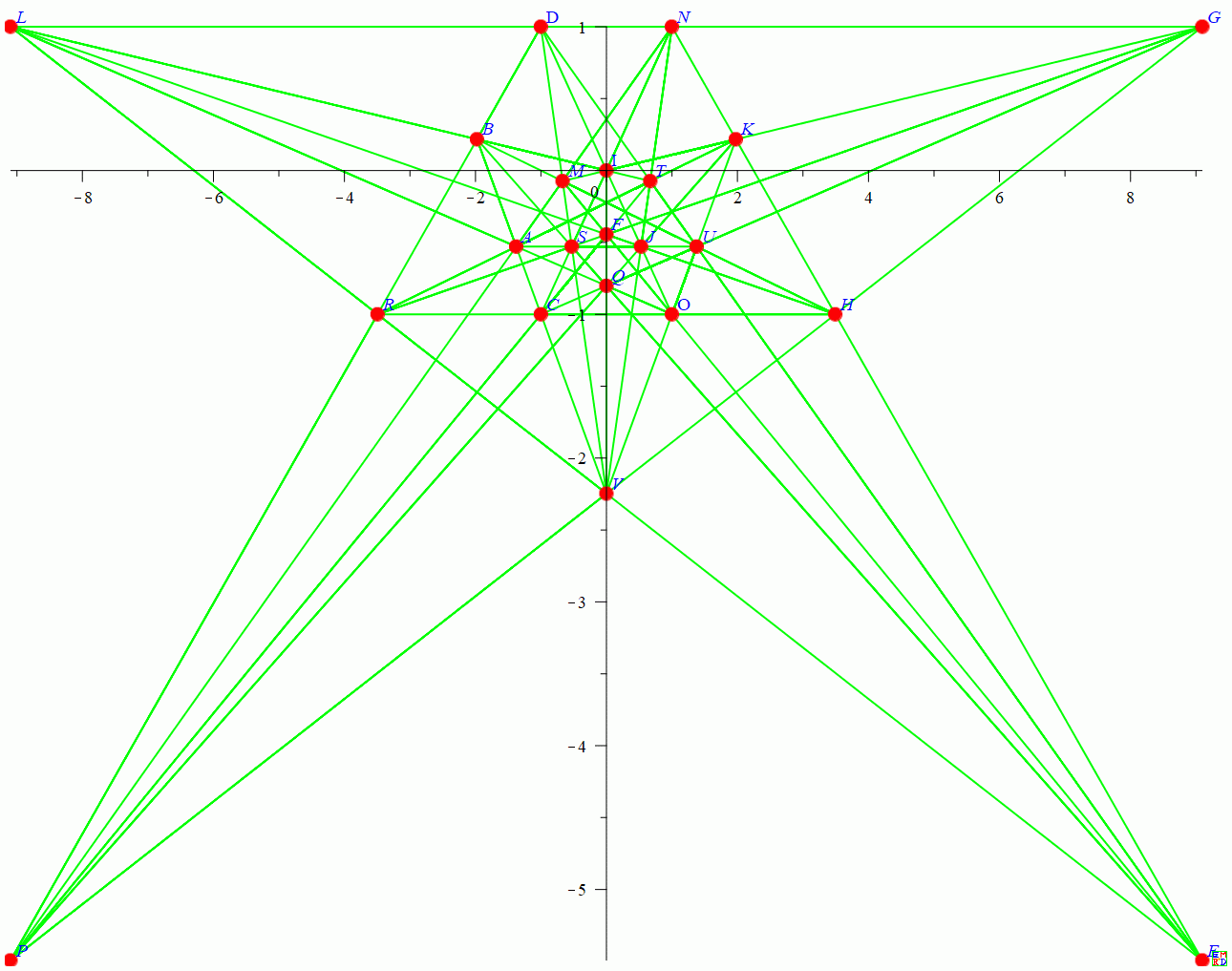
对于92# 22棵28行计算结果：

第一种变换：
变换基点
D[-1.246979604, 2.801937736, 1]->[-1, 1, 1]
C[1, 1., 0]-> [-1, -1, 1]
O[0, 0, 1]-> [1, -1, 1]
N[-0.2469796037, 1.554958132]-> [1, 1, 1]
变换矩阵
[[-0.450167919201864,-6.11795566442781 10^(-12),-0.249824347570890],[-0.172883812629957,-0.277284106578026,0.249824347570891],[0.326764882492357,0.123403036715626,-0.249824347570890]]
变换后坐标
[-1.37765085332385, -0.529077088429172, A], [-1.97612527388360, 0.217208307592350, B], [-0.999999999999999, -1.00000000000000, C], [-1.00000000000000, 1.00000000000000, D], [9.09783467661472, -5.49395920780248, E], [1.01624779636810*10^(-11), -0.445041867836675, F], [9.09783468145604, 1.00000000089177, G], [3.49395920794733, -1.00000000000000, H], [2.49168866775879*10^(-11), 4.24915273456024*10^(-10), I], [0.529077088568819, -0.529077088421778, J], [1.97612527418754, 0.217208307850663, K], [-9.09783467826472, 1.00000000025303, L], [-0.669362319332739, -0.0735738055107096, M], [1.00000000000000, 0.999999999999999, N], [0.999999999999999, -1.00000000000000, O], [-9.09783468215043, -5.49395920920715, P], [-1.66965331189807*10^(-12), -0.801937735764155, Q], [-3.49395920747015, -0.999999999999997, R], [-0.529077088614249, -0.529077088425881, S], [0.669362319345955, -0.0735738053613482, T], [1.37765085336987, -0.529077088418488, U], [-4.95770268484256*10^(-11), -2.24697960405147, V]
作图得到：


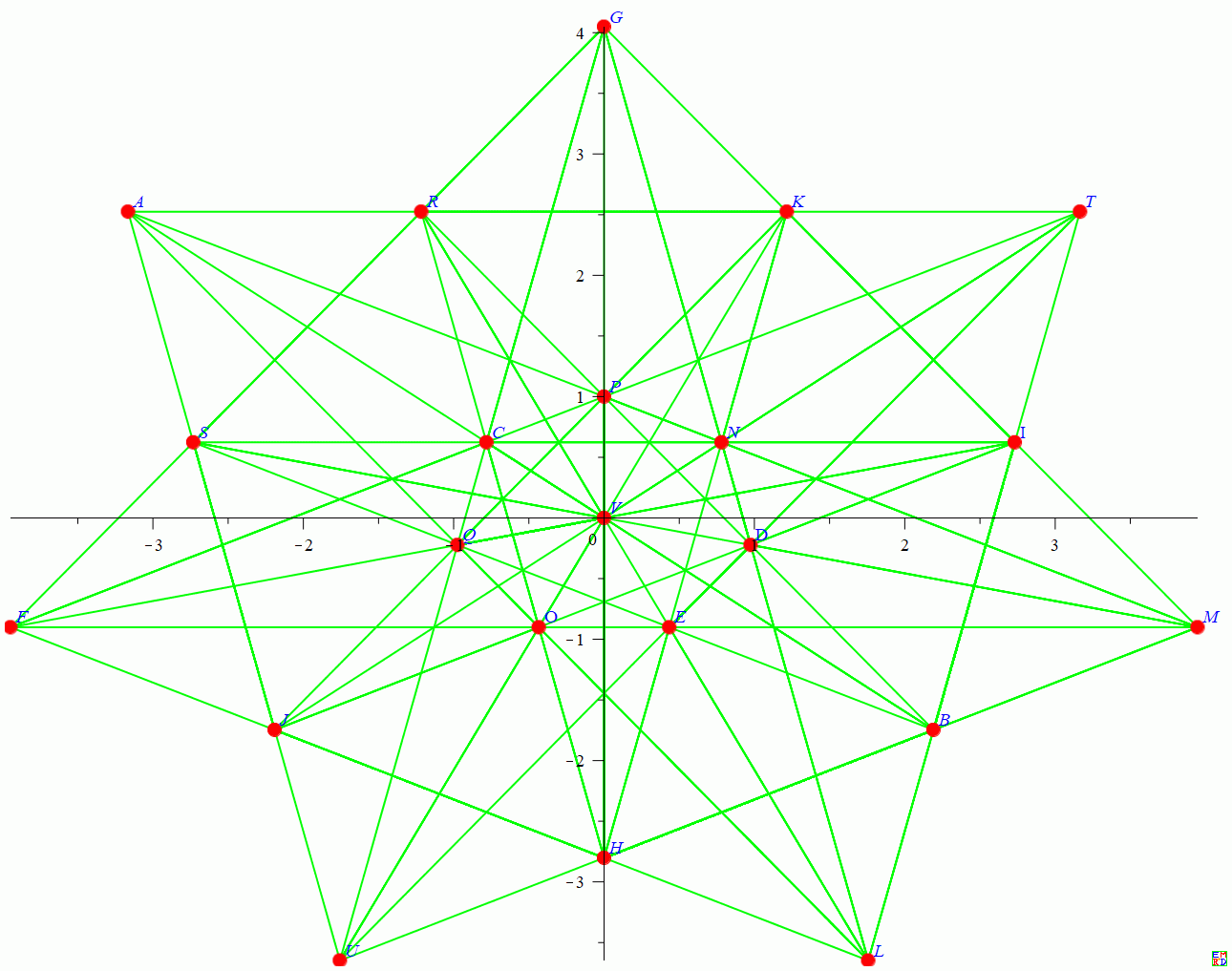
第二种变换：
变换基点
Q[-0.5549581321, 0, 1]->[-cos((4*Pi)/7 - Pi/2), -sin((4*Pi)/7 - Pi/2), 1]
C[1, 1., 0]->[-cos(Pi/2 - (2*Pi)/7), sin(Pi/2 - (2*Pi)/7), 1]
P[0.3079785284, 1.554958132, 1]->[0, 1, 1]
N[-0.2469796037, 1.554958132, 1]->[cos(Pi/2 - (2*Pi)/7), sin(Pi/2 - (2*Pi)/7), 1]
变换矩阵
[[0.368159794960638,-1.49785357275766 10^(-10),-0.113385311635113],[-0.293597639237085,-7.30443255538140 10^(-11),-0.235447026039259],[-0.116301226369752,-0.354592825735578,0.261326483448076]]
变换后坐标
[-3.16557104729199, 2.52445866996847, A], [2.19064313584455, -1.74697960385784, B], [-0.781831482400001, 0.623489802000000, C], [0.974927912667662, -0.222520933680391, D], [0.433883739946211, -0.900968867700935, E], [-3.94740253426969, -0.900968869732383, F], [-1.28790847455459*10^(-9), 4.04891733294242, G], [1.60599572875655*10^(-9), -2.80193773915855, H], [2.73168730180842, 0.623489801239610, I], [-2.19064313609670, -1.74697960662040, J], [1.21571521948805, 2.52445866684164, K], [1.75675939804009, -3.64794847417938, L], [3.94740252803703, -0.900968867171479, M], [0.781831482400000, 0.623489801999999, N], [-0.433883738605629, -0.900968868262603, O], [4.25870412252069*10^(-17), 1.00000000000000, P], [-0.974927912200001, -0.222520934000000, Q], [-1.21571522162583, 2.52445866857690, R], [-2.73168730901066, 0.623489802421985, S], [3.16557103905028, 2.52445866545007, T], [-1.75675939661644, -3.64794847941973, U], [4.22415081199252*10^(-10), 2.05994933491079*10^(-10), V]
作图得到：

数学星空

mathe 发表于 2019-12-20 20:53
113#的一些解也可以试验一下，比如:
ADGJBEIJCDHKAFIKCEGLBFHLCJMODINODLMPAHNPGKOPBGMQFJNQAEOQEHMRBKNRC ...

127#提到的问题：

以AIFK为基点变换成正方形四个顶点得到的图形太丑陋了！

因此换了一种基点变换

D[1., 1.61803398850000, 0.]->[-1, 1, 1]
Q[1., -1.61803398850000, 1.]-> [-1, -1, 1]
S[1.61803398850000, 1., 1.]-> [1, -1, 1]
J[0., 1., 0.]->[1, 1, 1]

变换矩阵
[[0.0884727823300127,0.0884727821700312,-0.0884727823794497],[-0.374776719546547,0.0884727821700311,0.374776719497110],[-0.374776719546547,0.0884727821700311,0.661080656812519]]

变换后坐标
[-0.236067977853743, 1.00000000000000, A], [-2.79390978395961*10^(-10), 0.618033988738628, B], [-0.0786893261452451, 0.745355992504937, C], [-1.00000000000000, 1.00000000000000, D], [-0.447213595738054, 0.447213595547152, E], [-1.72672981734630*10^(-10), -1.72672593956860*10^(-10), F], [0.236067977163050, 1.00000000000000, G], [-2.97620595116178*10^(-10), 0.723606797717698, H], [-0.133830541655888, 0.566915270678380, I], [1.00000000000000, 1.00000000000000, J], [-0.182743997952620, 0.774115996442465, K], [-3.12368638987683*10^(-10), 0.809016994363016, L], [0.105572808694640, 0.788854381992946, M], [0.333333333179846, 0.333333333179846, N], [-0.358570173921346, 0.679285086849915, O], [-0.0871677260125080, 0.825664548605471, P], [-0.999999999999997, -0.999999999999995, Q], [-0.0717140350265245, 0.679285086803935, R], [0.999999999999998, -0.999999999999997, S], [0.0871677253820215, 0.825664548605471, T]

作图得到：

数学星空

mathe 发表于 2019-12-24 15:13
75#的20棵树23行可以做出一种更加对称的形式，只是直线CDJK是无穷远直线:

对于这个情况可以得到：

变换基点：

T[0.4450418679, 1., 1]->[-1, 1, 1]
P[0.8019377358, 0.6431041321, 1]->  [-1, -1, 1]
S[0.5549581321, 1.445041868, 1]->[1, -1, 1]
R[1., 1., 1]-> [1, 1, 1]

变换矩阵

[[-0.0432831484963104,-0.0432831485356885,-0.0347103901407741],[-0.393782929673780,0.151229555324098,0.121276687176910],[-0.393782929673780,-0.393782929634402,0.666289172135409]]

变换后坐标

[0.356895867885345, -9.17957205380134*10^(-11), A], [0.109916264149943, 0.384042943271934, B], [-0.286208264194413, -1.00000000012933, C], [-0.286208264231225, -0.286208264216836, D], [-0.445041867958698, -1.61657463873974*10^(-11), E], [0.109916264260934, -1.00000000009112, F], [-0.198062264217136, 2.07729034328235*10^(-11), G], [0.109916264211538, -0.384042943315251, H], [0.109916264100547, 1.00000000000000, I], [-0.286208264297558, 1.00000000000000, J], [-0.286208264260746, 0.286208264220178, K], [-5.87429297921351*10^(-12), -5.84312697869233*10^(-12), L], [-0.0520950836249219, 0.182018097019687, M], [-0.131166769277656, 0.217208307702169, N], [-0.131166769250385, -0.217208307721898, O], [-1.00000000000000, -1.00000000000000, P], [-0.0520950835999899, -0.182018097022159, Q], [0.999999999999999, 1.00000000000000, R], [1.00000000000000, -1.00000000000000, S], [-0.999999999999999, 1.00000000000000, T]

画图得到：

mathe

转化自https://www2.stetson.edu/~efriedma/trees/ 的23棵树28行整数解

        A(+0,+0)
        B(1/3,+1)
        C(1/2,3/2)
        D(5/6,5/2)
        E(-1/6,1/2)
        F(+0,+1)
        G(1/3,2)
        H(1/2,5/2)
        I(-1/6,3/2)
        J(+0,2)
        K(-1/6,5/2)
        L(-1,4)
        M[+1,1,0];
        N[+1,+0,0];
        O[+1,-1,0];
        P[+0,+1,0];
        Q(+1,+0)
        R(+1,+1)
        S(5/6,1/2)
        T(+1,2)
        U(5/6,3/2)
        V(1/2,1/2)
        W(1/3,+0)

wayne

数学星空 发表于 2019-12-25 22:24
对于这个情况可以得到：

变换基点：

1）浮点数不太靠谱，可否贴出代数数。
2）图可以做的再精致一点。尽量对称一些，然后咱们论坛的博客就可以直接拿来引用了

mathe

对前面23棵28行添加一棵树两行得到24棵30行

mathe

25棵32行整数解:
        A(+1,3/2)
        B[+0,+1,0];
        C(+1,+0)
        D(+1,2/3)
        E(3/2,2)
        F[+1,2,0];
        G(3/4,1/2)
        H(5/6,2/3)
        I(+0,+0)
        J(1/2,1/2)
        K(1/2,2/3)
        L(5/12,5/6)
        M(3/2,+1)
        N[+1,+0,0];
        O(+0,+1)
        P(3/4,+1)
        Q(3/10,6/5)
        R(5/16,5/4)
        S(1/4,3/2)
        T[+1,-1,0];
        U(+0,2)
        V(5/4,1/2)
        W(3/2,+0)
        X(1/2,2)
        Y(3/4,3/2)
ABCDAFJPANSYAMTXBEMWBFNTBIOUBJKXBGPYCFMVCINWCJOTCHPXCGSUDGIMDHKNDPUWEFGHEIKPENUXEOQYFILYFOSXGJNVGKOWHLOVHQTWIQRXJLRSMNOPPSTVVWXY