数学研发网设为首页收藏本站
切换到窄版

 找回密码
 欢迎注册
数学研发论坛»论坛 › 【数学研究】 › 数学欣赏 › 果树种植最优解精美图形作法探讨
1 ...67891011121314... 18下一页
返回列表 发新帖
楼主: wayne

[讨论] 果树种植最优解精美图形作法探讨

 火 [复制链接]
wayne
 楼主| 发表于 2019-12-11 14:32:57 | 显示全部楼层
22棵树28行
  1. ABCVKOUVJNTVDMSVELRVGHPVFIQVALOQAMNPAJSUAKRTJKPQEHKNDIJOFHJLGIKMDETUEFMODGLNFGRSCHORCINSBHMUBILTBEQSBDPRCGQUCFPT
  2. +1-1*Uy+1*Tx*Uy-1*Uy*Uy,+1*Tx+1*Uy-1*Uy*Uy,+1*Tx*Tx+1*Uy-2*Uy*Uy,+1+1*Sx-1*Tx,+1*Qx+1*Uy,-1+1*Py-1*Uy,+1*Px-1*Tx-1*Uy,-1+1*Iy+1*Tx,+1*Hy-1*Tx-1*Uy,+1*Gy-1*Tx-2*Uy,-1+1*Fy+1*Tx+1*Uy,-1+1*Cy,+1+1*Ey-1*Tx,-2+1*Dy+1*Tx-1*Uy,+1*By-1*Tx+1*Uy,+1*Fx+1*Uy,-1+1*Ny-1*Uy,+1*Sy-1*Uy,-1+1*Rx,+1*Ix+1*Uy,-1+1*My-1*Uy,+1*Gx-1*Tx-1*Uy,+1*Jy-1*Uy,+1*Nx-1*Tx,+1+1*Mx-1*Tx,+1*Jx-1*Tx,-1+1*Ty,+1*Hx-1*Tx-1*Uy,-1+1*Ex,+1+1*Dx-1*Tx,-1+1*Ry
  3. Tx,Uy,Sx,Qx,Py,Px,Iy,Hy,Gy,Fy,Cy,Ey,Dy,By,Fx,Ny,Sy,Rx,Ix,My,Gx,Jy,Nx,Mx,Jx,Ty,Hx,Ex,Dx,Ry
  4. Ax=1,Ay=0,Az=0,Bx=1,Bz=0,Cx=1,Cz=0,Kx=0,Ky=1,Lx=1,Ly=0,Ox=0,Oy=0,Qy=0,Ux=0,Vx=0,Vy=1,Vz=0,
复制代码

  1. {{1, 0, 0}, {1, -2*Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 0}, {1, 1, 0},
  2.   {-1 - Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 2 + 2*Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] - Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 1},
  3.   {1, -1 - Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 1}, {-Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0], 1 - Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 1},
  4.   {Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 1},
  5.   {Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 1}, {-Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0],
  6.    1 + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] - Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 1}, {-Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2,
  7.    Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0], 1}, {0, 1, 1}, {1, 0, 1}, {-1 - Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2,
  8.    1 + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0], 1}, {-Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 1 + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0], 1},
  9.   {0, 0, 1}, {Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 1 + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0], 1}, {-Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0], 0, 1}, {1, 1, 1},
  10.   {-1 - Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0], 1},
  11.   {-Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0] + Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0]^2, 1, 1}, {0, Root[1 - #1 - 2*#1^2 + #1^3 & , 1, 0], 1}, {0, 1, 0}}
复制代码

2.png

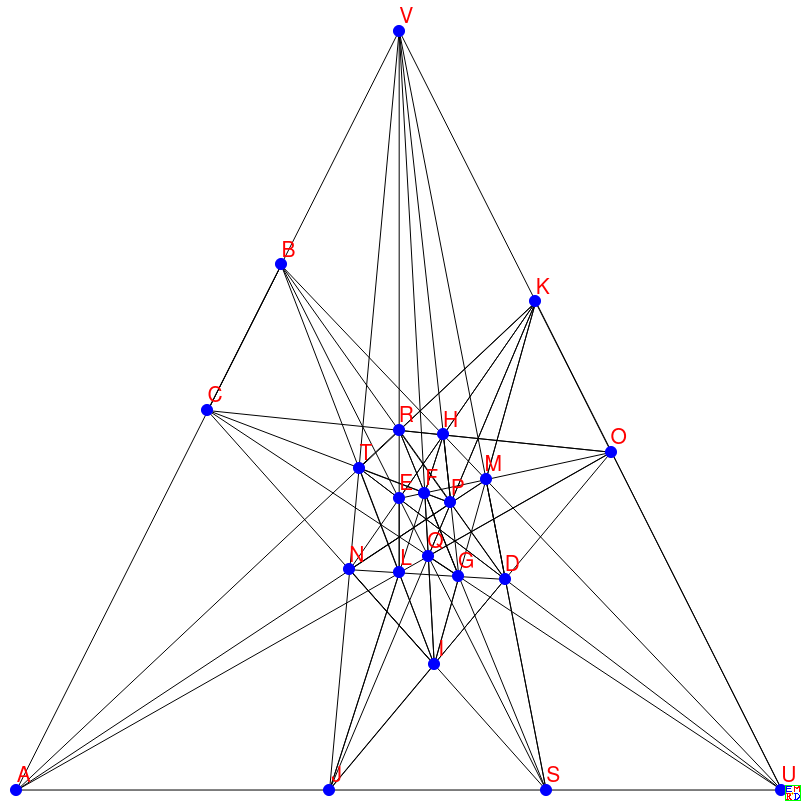
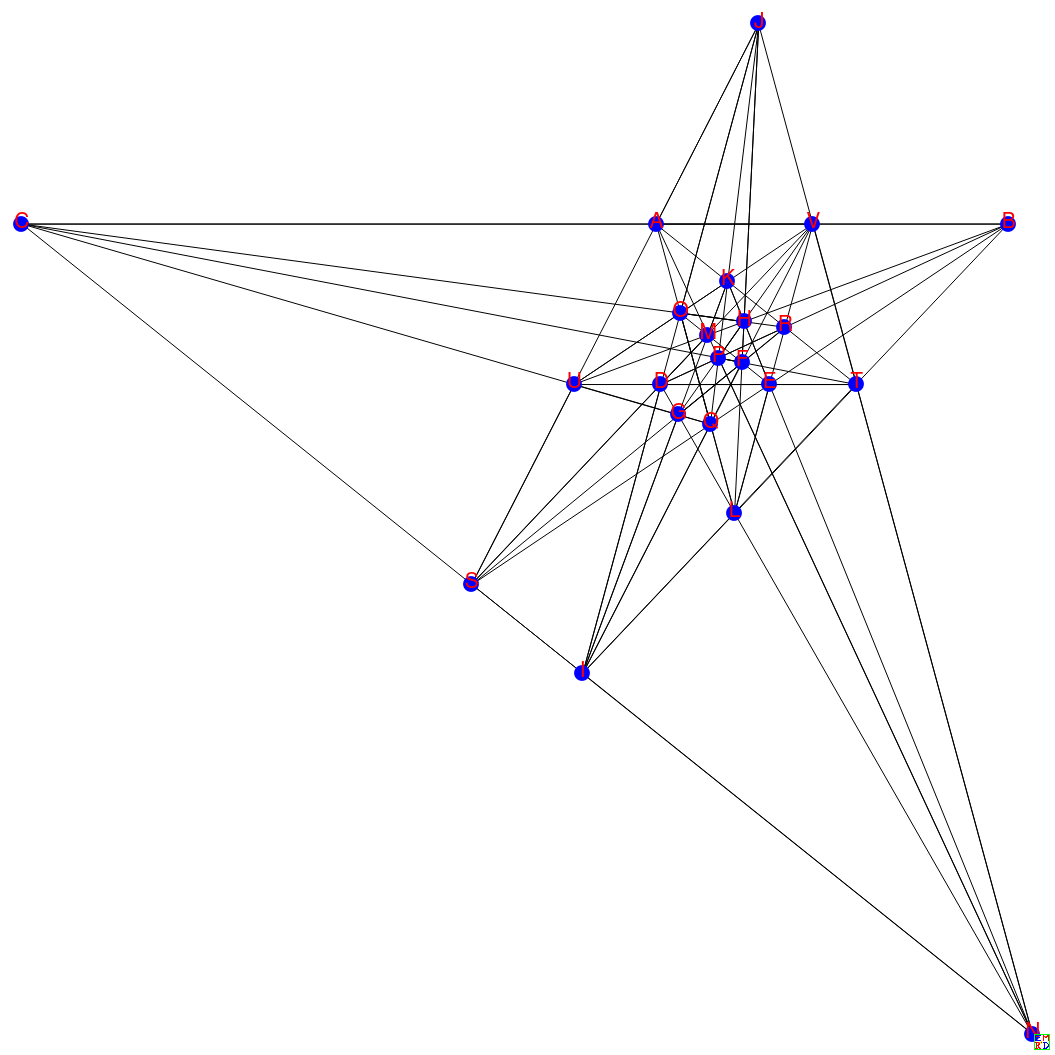
另外还有一个等价的图形:

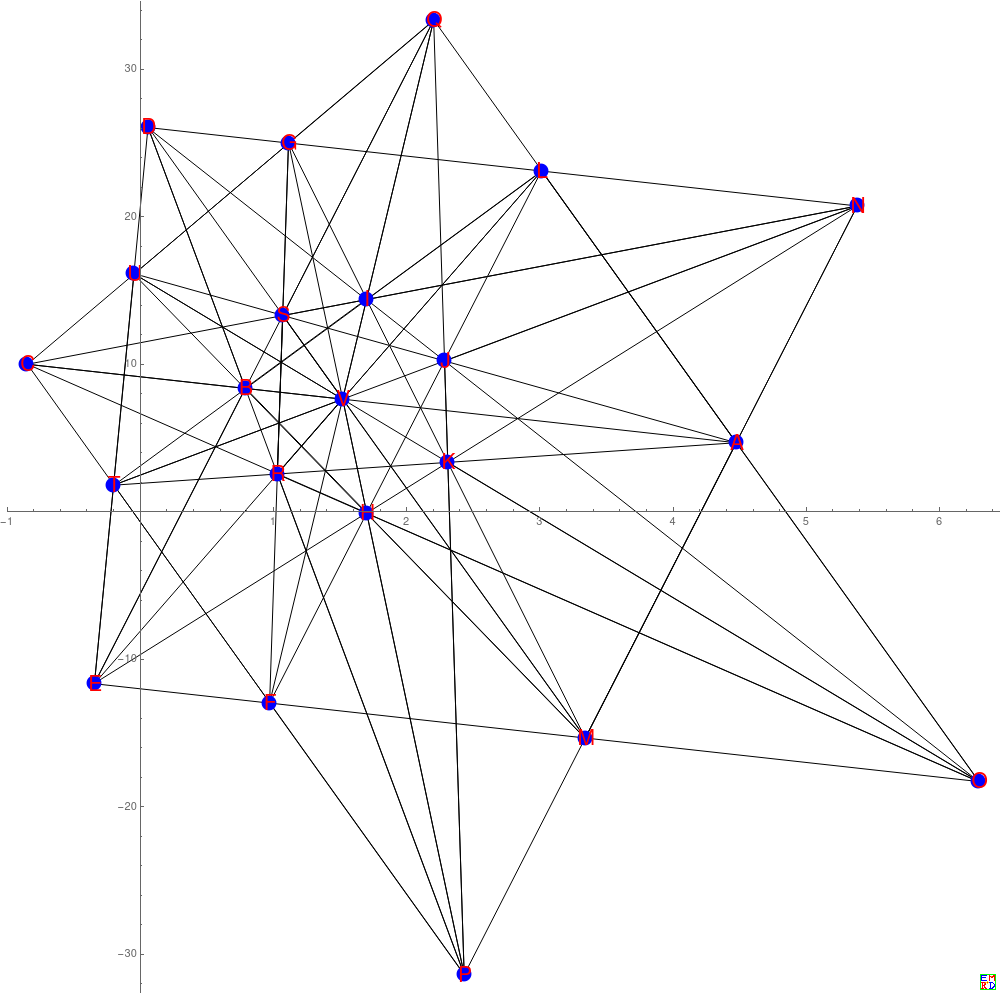
3.png 11.png


毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-11 14:47:38 来自手机 | 显示全部楼层
最后一个很赞，能画成七个方向全对称吗？
这个结果应该很重要。
主贴170楼有16棵15行的图，可以将那个画成五个方向全对称，看看两者是否有关联
https://bbs.emath.ac.cn//thread-703-1-1.html

点评

mathe
是的，肯定是正七边形，我现在搜索的是超对称的解，不过发现大部分是复数解。  发表于 2019-12-11 20:51
wayne
规律是 外层是 正七角形,内层是正七边形  发表于 2019-12-11 18:22
wayne
问题不大, 我有空再推敲一下  发表于 2019-12-11 15:30
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

wreck
发表于 2019-12-11 22:39:51 来自手机 | 显示全部楼层
应该是可以的，直接取正7边形的7个顶点即可。
Screenshot_2019-12-11-22-35-55-442_cn.wps.moffice_eng.png

点评

wayne
赞  发表于 2019-12-12 07:49
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

wreck
发表于 2019-12-11 22:56:03 来自手机 | 显示全部楼层
另外，在网址https://www2.stetson.edu/~efriedma/trees/
中，提供了一个比较美观的图形，不确定和170楼中的图形是不是等价的。
22-51-33-4pt16.gif
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

wayne
 楼主| 发表于 2019-12-12 07:49:27 | 显示全部楼层
wreck 发表于 2019-12-11 22:39
应该是可以的，直接取正7边形的7个顶点即可。


顶点的度数不匹配.  应该 就是这种类似的图形,赞
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-12 08:04:00 | 显示全部楼层
16点15边楼上的没错，但是更上面的图是21点21边，而我们要的是22点28边:
w22.7.png

评分

参与人数 1威望 +12 金币 +12 贡献 +12 经验 +12 鲜花 +12 收起 理由
wayne + 12 + 12 + 12 + 12 + 12 赞一个!

查看全部评分

毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-13 17:06:15 | 显示全部楼层
24棵30行的例子
o24.1.png
        [+1*t^2-1/5]
        A(1/2-5*t/2,5*t/2-1/2)
        B(1/2-5*t/2,-5/2*t-3/2)
        C(5*t/2-3/2,-5*t/2+1/2)
        D(5*t/2+3/2,-5*t/2-1/2)
        E(5*t/2-1/2,3/2-5*t/2)
        F(-5*t/2-1/2,-5*t/2+1/2)
        G(+1,+1)
        H(-5*t,-1)
        I(+1,-1)
        J(-1,-5*t)
        K(-1,+1)
        L(-t,-t)
        M[+0,+1,0];
        N(1/2-5*t/2,-1)
        O(+1,+0)
        P(+0,+1)
        Q[+1,+0,0];
        R(-1,-5*t/2+1/2)
        S[+1,5*t/2+1/2,0];
        T(+0,+0)
        U[+1,5*t/2-1/2,0];
        V(+0,-5*t/2-1/2)
        W(-5*t/2-1/2,+0)
        X(-5*t/2-1/2,-5*t/2-1/2)
MQSUMPTVNOUXNRVWOQTWPRSXJKMRGIMOJLNPHINQHLORGKPQIJUVGLTXHKSWFMWXCNSTERTUAPUWDQVXBOSVCKLVFGHUAIKTDILWBHJXEGJSABMNCFQRDEOP
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

wayne
 楼主| 发表于 2019-12-13 17:27:57 | 显示全部楼层
我也同步的画一下 :
24棵树30行
  1. MQSUMPTVNOUXNRVWOQTWPRSXJKMRGIMOJLNPHINQHLORGKPQIJUVGLTXHKSWFMWXCNSTERTUAPUWDQVXBOSVCKLVFGHUAIKTDILWBHJXEGJSABMNCFQRDEOP
复制代码

123.png

点评

数学星空
你是如何构造射影变换将无穷远点变为普通点的啊？本例的变换矩阵是什么呢?  发表于 2019-12-19 15:49
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-13 17:45:42 | 显示全部楼层
这两个呢？
        [+1*t^2-1*t-1]
        A(+0,+1)
        B(-t-1,1/2)
        C(2*t+1,3*t/2+1)
        D(2*t-1,t/2)
        E(t+1,-t/2)
        F(+1,+0)
        G(+1,1-t/2)
        H(-2*t-1,-t/2)
        I(t,1/2)
        J(+0,t/2+1/2)
        K[+1,-t/2,0];
        L[+1,t/2,0];
        M(-1,t/2)
        N(2*t+1,t/2+1)
        O(t,1/2-t/2)
        P(t,+0)
        Q(t+1,t/2+1/2)
        R(-t,t/2+1/2)
        S(2*t+1,-t/2)
        T(+0,+0)
        U[+0,+1,0];
        V[+1,+0,0];
        W(+1,t/2)
        X(t+1,1/2)
IOPULNOXJQRVKMRTHNQWGMPSKLUVGHTXIJSWAGKOBHLRFILQDGINCHJMEJKPAJTUBIVXFGUWCLTWDKSXEHSVARWXBOSTEQUXDMVWFPTVCNSUABMNEFORCDPQ

        [+1*t^2-2*t+1/2]
        A[+0,+1,0];
        B(4*t/7+4/7,3/7-4*t/7)
        C(3-t,-1/2)
        D(2*t-1,1-t)
        E(4*t-6,3-2*t)
        F(8-4*t,-1)
        G(t,1/2-t)
        H(5-2*t,1-t)
        I(4*t/7+2/7,-2*t/7-1/7)
        J(2*t-2,3-2*t)
        K(2*t-2,1-t)
        L(2*t-2,-1)
        M(+0,+1)
        N[+1,t-1,0];
        O(2,3-2*t)
        P(+1,t-2)
        Q(+1,+0)
        R(2,+0)
        S[+1,+0,0];
        T(+0,+0)
        U(2,1-2*t)
        V(+1,-t)
        W[+1,1-t,0];
        X(+0,-1)
ANSWAMTXAPQVAORUAJKLQRSTUVWXCJNRBJMQEJOSDJPTENPXDMOWFLSXGLTWHLRVILQUBFKRCGKQEIKTDHKSBIOXCHPWEFMUDGNVFHNOGIMPCFIVBGHUBCDE
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-13 17:48:14 | 显示全部楼层
另外
        +1*v14*v15-2*v14-1*v15+1*v16+1*v17
        +1*v1*v14+1*v14-1*v15-3*v16-1*v17+3
        +1*v1*v17+1*v14-1*v15-2*v16-1*v17+2
        +1*v7+1*v14-2*v15-1*v17+1
        +1*v10*v14-1*v10*v17-1*v14+2*v15-1*v16+1*v17-1
        +1*v0*v15-1*v0+1*v14-3*v15+1*v16-1*v17+2
        +1*v1*v15-1*v1+1*v14-2*v15-1*v16-1*v17+3
        +1*v10*v15-1*v10+1*v14-3*v15+1*v16-1*v17+2
        +1*v15^2+2*v14-1*v15-1*v16-2*v17+1
        +1*v0*v16-1*v0-1*v14+3*v15-2*v16+1*v17-1
        +1*v1*v16-1*v1+1*v14-1*v15-3*v16-1*v17+4
        +1*v10*v16-1*v10-1*v14+3*v15-2*v16+1*v17-1
        +1*v14*v16-2*v14+1*v15+1*v17-1
        +1*v15*v16+1*v14-1*v15-1*v16-1*v17+1
        +1*v16^2+1*v15-2*v16
        +1*v15*v17-6*v14-2*v15+3*v16+5*v17-1
        +1*v16*v17-3*v14+1*v16+2*v17-1
        +1*v2-1*v14-1*v15+1
        +1*v3-1*v15+1*v16-1
        +1*v4+1*v14-3*v15+1*v16-1*v17+1
        +1*v5-2*v14+1*v16+1*v17-1
        +1*v6-2*v14-1*v15+1*v16+1*v17
        +1*v8-1*v14+1*v16-1
        +1*v9-1*v14+1*v15+2*v16+1*v17-4
        +1*v11+1*v14-3*v15-1*v17+2
        +1*v12-1*v15-1*v17+1
        +1*v13-2*v14+1*v15+1*v17-1
        +1*v0*v14-1*v0*v17-1*v14+2*v15-1*v16+1*v17-1
        +1*v14^2-1*v17^2-17*v14-3*v15+7*v16+17*v17-4
        +1*v14*v17-1*v17^2-14*v14-3*v15+6*v16+14*v17-3
        A[+1,v0,0];
        B(v2,v9)
        C(v2,v3)
        D(+1,+0)
        E(+0,+1)
        F(v5,v4)
        G(+0,v10)
        H(v6,v11)
        I(v12,v7)
        J[+1,v1,0];
        K(v8,+0)
        L(v13,v4)
        M(v14,+1)
        N(v5,v3)
        O(v2,v4)
        P[+1,+0,0];
        Q(v6,v15)
        R(v5,v16)
        S(v6,v3)
        T(+0,+0)
        U(v17,v7)
        V(v8,+1)
        W[+0,+1,0];
        X(v8,v7)
AJPWAIQVAHRXFGUVEFSXEGTWDKPTCKQUBKRSBDNVCDMXBCOWFLOPGLMRELNQHIOTHJNUIJMSAMNOLSTUKVWXIPUXJRTVHQSWCNPSDORUBMQTEMPVGOQXFNRW
和
        +1*v18*v19+1/2*v18+3/2*v19-1*v20
        +1*v1+3*v19-1*v20-1*v21+1
        +1*v3-1*v19-1*v21
        +1*v4+1*v19-1*v20-1*v21
        +1*v5-1*v18-2*v19+2*v20+2*v21-1
        +1*v6+1*v18+1*v19-1*v20+1*v21-1
        +1*v7+1*v19-1*v20+1*v21-1
        +1*v8+1*v19+1*v21-1
        +1*v18^2+1*v19-1*v21
        +1*v18*v20+1*v18+3*v19-2*v20-1*v21
        +1*v19*v20+1*v21
        +1*v18*v21-1/2*v18+1/2*v19
        +1*v20*v21+1*v19-1*v20
        +1*v0-1*v18+1
        +1*v2-1*v18-1*v19+1*v20-1*v21
        +1*v9-1*v18-2*v19+1*v20
        +1*v11+1*v18-1*v20
        +1*v12-1*v19+3*v21-1
        +1*v13+1*v18+2*v19-2*v20-2*v21
        +1*v14+3*v19-2*v20-1*v21-1
        +1*v15+2*v21-1
        +1*v16-2*v19+1*v20+2*v21-1
        +1*v17-1*v18+1*v19+1*v21-1
        +1*v19^2-3/8*v18-3/8*v19+1/4*v20+3/4*v21
        +1*v20^2+1*v18+1*v19-1*v20+1*v21
        +1*v19*v21-1/8*v18-1/8*v19-1/4*v20+1/4*v21
        +1*v21^2-3/8*v18-3/8*v19+1/4*v20-1/4*v21
        +1*v10-4*v19+2*v20+4*v21-1
        A[+0,+1,0];
        B(v8,v9)
        C(v10,v11)
        D(v12,v13)
        E(+1,+0)
        F(v14,v2)
        G(v15,v3)
        H(v16,v4)
        I(v17,v3)
        J(v5,+0)
        K(v5,v2)
        L(+0,+1)
        M[+1,+0,0];
        N(v6,v18)
        O(v7,v4)
        P(v5,v19)
        Q(+0,v3)
        R[+1,v0,0];
        S[+1,v1,0];
        T(+0,+0)
        U(v6,v20)
        V(v7,v2)
        W(v6,v4)
        X(v7,v21)
AMRSALQTAOVXANUWAJKPGPRXFPQWILNXHMOWFKMVGKLUEJMTDJLSBOTUCNSVBJNRCJOQDGTVEFSUGIMQFHLRDIOREHNQDEWXBHPVCIPUBGSWCFTXBEIKCDHK
方程没有解完，还不能判断是否有实数解
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

1 ...67891011121314... 18下一页
返回列表 发新帖
高级模式
B Color Image Link Quote Code Smilies
您需要登录后才可以回帖 登录 | 欢迎注册

本版积分规则

小黑屋|手机版|数学研发网 ( 苏ICP备07505100号 )

GMT+8, 2024-4-20 17:46 , Processed in 0.064529 second(s), 18 queries .

Powered by Discuz! X3.5

© 2001-2024 Discuz! Team.

快速回复 返回顶部 返回列表