果树种植最优解精美图形作法探讨

mathe

取t为方程$t^3-t^2-2*t+1=0$的根 0.44504186791262880857780512899358951893
正方形边长为1， ${VA}/{AQ}=1-t, {VF}/{FU}=t$。
自同构群（36阶）:
AJPWAIQVAHRXFGUVEFSXEGTWDKPTCKQUBKRSBDNVCDMXBCOWFLOPGLMRELNQHIOTHJNUIJMSAMNOLSTUKVWXIPUXJRTVHQSWCNPSDORUBMQTEMPVGOQXFNRW
Start group:
ABCDEFGHIJKLMNOPQRSTUVWX 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
BEGLAHJKDCFIMQTOVSXPUNWR 11 09 08 16 02 00 12 03 04 14 13 05 15 17 01 06 07 10 26 21 29 25 24 20 28 19 27 18 22 23
EAJIBKCFLGHDMVPTNXROUQWS 05 14 04 07 08 11 15 16 02 01 17 00 06 10 09 12 03 13 27 25 23 19 28 29 22 21 18 26 24 20
DGFLAJIKCBEHORUNXTWQSMVP 09 10 06 17 00 01 14 04 05 13 12 03 16 15 02 07 08 11 25 23 27 24 26 20 29 19 28 18 21 22
GAIHDKBELFJCOXQUMWPNSRVT 03 13 05 08 06 09 16 17 00 02 15 01 07 11 10 14 04 12 28 24 22 19 29 27 21 23 18 25 26 20
LJHIBCDFGEAKTSUQRPWVXMNO 14 13 12 10 11 09 01 02 00 17 15 16 07 06 08 03 04 05 19 20 18 28 27 29 23 21 22 26 25 24
CFELAIHKBDGJNPSMWUVRTOXQ 10 11 07 15 01 02 13 05 03 12 14 04 17 16 00 08 06 09 24 22 28 26 25 20 27 19 29 18 23 21
JBDKLFEAIHCGTRVUMWOQXSNP 16 17 00 04 12 14 07 10 11 08 06 09 03 05 13 01 02 15 22 28 24 21 23 18 25 20 26 19 27 29
FAHJCKDGLEIBNWRSOVQMTPXU 04 12 03 06 07 10 17 15 01 00 16 02 08 09 11 13 05 14 29 26 21 19 27 28 23 22 18 24 25 20
ICKDEGLHJABFPXUVSOWNRMQT 01 17 15 13 05 14 09 08 11 10 06 07 03 12 04 16 02 00 21 29 26 22 18 23 20 25 24 27 19 28
HBKCGFLJIADEQWSXTNVMPORU 02 15 16 12 03 13 10 06 09 11 07 08 04 14 05 17 00 01 23 27 25 21 18 22 20 24 26 28 19 29
KEFGJHICDBLAVWXRPQNMOTSU 08 06 07 15 16 17 13 12 14 05 03 04 02 01 00 10 11 09 20 18 19 25 26 24 29 28 27 22 21 23
ADBCGEFJHIKLOMNQRPTUSXVW 01 02 00 04 05 03 07 08 06 10 11 09 14 12 13 16 17 15 18 19 20 23 21 22 26 24 25 28 29 27
BLEGJAHCKDFITMQVSOPUXRNW 09 08 11 02 00 16 03 04 12 13 05 14 01 15 17 07 10 06 26 21 29 20 25 24 27 28 19 22 23 18
EIAJCBKGFLHDPMVNXTOURSQW 14 04 05 08 11 07 16 02 15 17 00 01 09 06 10 03 13 12 27 25 23 29 19 28 18 22 21 24 20 26
DLGFIAJBKCEHUORXTNQSWPMV 10 06 09 00 01 17 04 05 14 12 03 13 02 16 15 08 11 07 25 23 27 20 24 26 28 29 19 21 22 18
GHAIBDKFELJCQOXMWUNSPTRV 13 05 03 06 09 08 17 00 16 15 01 02 10 07 11 04 12 14 28 24 22 27 19 29 18 21 23 26 20 25
LIJHDBCEFGAKUTSRPQVXWOMN 13 12 14 11 09 10 02 00 01 15 16 17 08 07 06 04 05 03 19 20 18 29 28 27 22 23 21 25 24 26
CLFEHAIDKBGJSNPWUMRTVQOX 11 07 10 01 02 15 05 03 13 14 04 12 00 17 16 06 09 08 24 22 28 20 26 25 29 27 19 23 21 18
JKBDELFHAICGVTRMWUQXOPSN 17 00 16 12 14 04 10 11 07 06 09 08 13 03 05 02 15 01 22 28 24 18 21 23 26 25 20 27 29 19
FJAHDCKEGLIBRNWOVSMTQUPX 12 03 04 07 10 06 15 01 17 16 02 00 11 08 09 05 14 13 29 26 21 28 19 27 18 23 22 25 20 24
IDCKLEGAHJBFUPXSOVNRWTMQ 17 15 01 05 14 13 08 11 09 06 07 10 04 03 12 02 00 16 21 29 26 23 22 18 24 20 25 19 28 27
HCBKLGFAJIDESQWTNXMPVUOR 15 16 02 03 13 12 06 09 10 07 08 11 05 04 14 00 01 17 23 27 25 22 21 18 26 20 24 19 29 28
KGEFIJHBCDLAXVWPQRMONUTS 06 07 08 16 17 15 12 14 13 03 04 05 00 02 01 11 09 10 20 18 19 24 25 26 27 29 28 21 23 22
ACDBFGEIJHKLNOMRPQUSTWXV 02 00 01 05 03 04 08 06 07 11 09 10 13 14 12 17 15 16 18 19 20 22 23 21 25 26 24 29 27 28
BGLEHJADCKFIQTMSOVUXPWRN 08 11 09 00 16 02 04 12 03 05 14 13 17 01 15 10 06 07 26 21 29 24 20 25 19 27 28 23 18 22
EJIAKCBLGFHDVPMXTNUROWSQ 04 05 14 11 07 08 02 15 16 00 01 17 10 09 06 13 12 03 27 25 23 28 29 19 21 18 22 20 26 24
DFLGJIACBKEHRUOTNXSWQVPM 06 09 10 01 17 00 05 14 04 03 13 12 15 02 16 11 07 08 25 23 27 26 20 24 19 28 29 22 18 21
GIHAKBDLFEJCXQOWUMSPNVTR 05 03 13 09 08 06 00 16 17 01 02 15 11 10 07 12 14 04 28 24 22 29 27 19 23 18 21 20 25 26
LHIJCDBGEFAKSUTPQRXWVNOM 12 14 13 09 10 11 00 01 02 16 17 15 06 08 07 05 03 04 19 20 18 27 29 28 21 22 23 24 26 25
CELFIHABDKGJPSNUMWTVRXQO 07 10 11 02 15 01 03 13 05 04 12 14 16 00 17 09 08 06 24 22 28 25 20 26 19 29 27 21 18 23
JDKBFELIHACGRVTWUMXOQNPS 00 16 17 14 04 12 11 07 10 09 08 06 05 13 03 15 01 02 22 28 24 23 18 21 20 26 25 29 19 27
FHJAKDCLEGIBWRNVSOTQMXUP 03 04 12 10 06 07 01 17 15 02 00 16 09 11 08 14 13 05 29 26 21 27 28 19 22 18 23 20 24 25
IKDCGLEJAHBFXUPOVSRWNQTM 15 01 17 14 13 05 11 09 08 07 10 06 12 04 03 00 16 02 21 29 26 18 23 22 25 24 20 28 27 19
HKCBFLGIAJDEWSQNXTPVMRUO 16 02 15 13 12 03 09 10 06 08 11 07 14 05 04 01 17 00 23 27 25 18 22 21 24 26 20 29 28 19
KFGEHIJDBCLAWXVQRPONMSUT 07 08 06 17 15 16 14 13 12 04 05 03 01 00 02 09 10 11 20 18 19 26 24 25 28 27 29 23 22 21

mathe

对于不少最优和较优结果，我们可以发现这些解具有强烈的对称性，也就是对树进行某种置换后，结果还是它自己本身，比如20棵树我们已知的三种结果有如下置换方案 (其中字母代表树的置换，而数字代表行的置换):
ADGJBEIJCDHKAFIKCEGLBFHLCJMODINODLMPAHNPGKOPBGMQFJNQAEOQEHMRBKNRCFPRILQRABCSDEFSGHITJKLTMNST
Start group:
ABCDEFGHIJKLMNOPQRST 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22
GHIJKLABCDEFNMOQPRTS 00 02 01 04 03 05 07 06 12 11 13 09 08 10 15 14 17 16 20 21 18 19 22
EDFBACIHGJLKNMQROPST 01 00 05 04 03 02 12 11 15 14 17 07 06 13 09 08 16 10 19 18 20 21 22
CBADFEKJLHGINMPORQST 02 05 00 04 03 01 09 08 07 06 10 15 14 16 12 11 13 17 18 19 21 20 22
IHGJLKEDFBACMNQORPTS 01 05 00 03 04 02 11 12 06 07 13 14 15 17 08 09 10 16 20 21 19 18 22
KJLHGICBADFEMNPROQTS 02 00 05 03 04 01 08 09 14 15 16 06 07 10 11 12 17 13 21 20 18 19 22
FDEBCALJKHIGMNRQPOST 05 02 01 03 04 00 14 15 11 12 17 08 09 16 06 07 13 10 19 18 21 20 22
LJKHIGFDEBCANMRPQOTS 05 01 02 04 03 00 15 14 09 08 16 12 11 17 07 06 10 13 21 20 19 18 22
        Parameter [-1+4*t+1*t^2=0]
        A[+1 ,0 , 0]
        B[0 ,+1 , +1]
        C[-1 ,+1 , +1]
        D[+1 ,-1/2-1/2*t , 0]
        E[0 ,+1/2+1/2*t , +1]
        F[+1 ,0 , +1]
        G[+1 ,-1/2+1/2*t , 0]
        H[+3/2+1/2*t ,-1/2-1/2*t , +1]
        I[0 ,0 , +1]
        J[0 ,+1 , 0]
        K[+1/2+1/2*t ,0 , +1]
        L[+1/2+1/2*t ,+1/2-1/2*t , +1]
        M[-1 ,+3/2-1/2*t , +1]
        N[+1 ,-1/2-1/2*t , +1]
        O[-1 ,+1/2+1/2*t , +1]
        P[+2+1*t ,-1/2-1/2*t , +1]
        Q[+1 ,+1/2+1/2*t , +1]
        R[+2/5+1/5*t ,+3/10-1/10*t , +1]
        S[-1/2-1/2*t ,+1 , +1]
        T[+1/2+1/2*t ,-1*t , +1]


ACEFDFHJBCIJBEHKADIKBFGMEJLMBDLNCGNODEGPFKNPAJOPAGLQCKMQCHLRDMOREIQRAHNSFIOSBPQSGHITABRTCDST
Start group:
ABCDEFGHIJKLMNOPQRST 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22
CDABFEGHIKJNPLQMOSRT 00 03 04 01 02 09 10 07 12 05 06 13 08 11 17 19 18 14 16 15 20 22 21
        A[+1 ,0 , 0]
        B[0 ,+1 , +1]
        C[0 ,+1 , 0]
        D[+1 ,0 , +1]
        E[+1 ,+1/2 , 0]
        F[+1 ,+2 , 0]
        G[-1 ,-1 , +1]
        H[+2 ,+2 , +1]
        I[0 ,0 , +1]
        J[0 ,-2 , +1]
        K[-2 ,0 , +1]
        L[+2 ,-1 , +1]
        M[-2 ,-3 , +1]
        N[-1 ,+2 , +1]
        O[-1 ,-2 , +1]
        P[-3 ,-2 , +1]
        Q[-2 ,-1 , +1]
        R[+2 ,+1 , +1]
        S[+1 ,+2 , +1]
        T[+1 ,+1 , +1]

BFHICDJKAEGLHJLMDGINAKMNFGKOCIMOEIKPBGMPBCLQFJNQADOQACHRBENRDLPRABJSEHOSCFPSDEFTGHQTIJRTKLST
Start group:
ABCDEFGHIJKLMNOPQRST 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22
BCAEFDIJKLGHMPNORSQT 01 02 00 03 08 09 04 05 06 07 13 15 14 16 18 17 10 11 12 19 21 22 20
CABFDEKLGHIJMOPNSQRT 02 00 01 03 06 07 08 09 04 05 16 17 18 10 12 11 13 15 14 19 22 20 21
HJAEIKFCDLGBQTONSRMP 01 02 00 10 19 20 06 12 04 11 16 22 17 13 21 14 03 07 05 08 18 15 09
JAHIKEDLGBFCQNTORMSP 02 00 01 10 04 11 19 20 06 12 13 14 21 03 05 07 16 22 17 08 15 09 18
LBJKGFEHICDARPTNSMQO 00 01 02 13 08 15 19 21 04 14 16 18 22 03 09 05 10 20 11 06 17 07 12
AHJKEIGBFCDLQONTMSRP 00 01 02 10 06 12 04 11 19 20 03 07 05 16 17 22 13 14 21 08 09 18 15
BJLGFKICDAEHRNPTMQSO 01 02 00 13 04 14 08 15 19 21 03 05 09 10 11 20 16 18 22 06 07 12 17
CLHIDGKAEBFJSPOTMRQN 02 00 01 16 08 18 06 17 19 22 03 09 07 13 15 21 10 12 20 04 05 14 11
HCLGIDFJKAEBSOTPQMRN 01 02 00 16 06 17 19 22 08 18 10 12 20 03 07 09 13 21 15 04 11 05 14
JLBFKGDAEHICRTNPQSMO 02 00 01 13 19 21 04 14 08 15 10 20 11 16 22 18 03 05 09 06 12 17 07
LHCDGIEBFJKASTPORQMN 00 01 02 16 19 22 08 18 06 17 13 21 15 10 20 12 03 09 07 04 14 11 05
        Parameter [+1-1*t-2*t^2+1*t^3=0]
        A[+1 ,+1-1*t , +1]
        B[+1 ,-1*t , 0]
        C[+1 ,0 , +1]
        D[+1*t^2 ,+1-1*t^2 , +1]
        E[+2+1*t-1*t^2 ,+1*t^2 , +1]
        F[+1 ,-1+2*t-1*t^2 , 0]
        G[-1-1*t+1*t^2 ,+1-1*t^2 , +1]
        H[0 ,+1 , 0]
        I[+1 ,0 , 0]
        J[0 ,+1 , +1]
        K[+1-1*t^2 ,+1*t^2 , +1]
        L[0 ,+1*t , +1]
        M[0 ,0 , +1]
        N[+1+1*t ,+1-1*t^2 , +1]
        O[+2+1*t-1*t^2 ,0 , +1]
        P[-1*t ,+1*t^2 , +1]
        Q[-1-1*t+1*t^2 ,+1+1*t-1*t^2 , +1]
        R[+1 ,+1 , +1]
        S[+2+1*t-1*t^2 ,-1*t+1*t^2 , +1]
        T[-1-1*t+1*t^2 ,+1 , +1]
也就是第一个结果的置换群是8阶的，第三个是12阶的，都有很强的对称性，而第二个是2阶的，应该代表只有轴对称。
由于对于超过20棵树，由于计算量过大，计算机已经很难去穷举了，所以我开始考虑能否只去寻找部分我们会比较感兴趣的解，而满足高度对称性的解看上去还不错，而且结果会比较漂亮。
为了搜索这种结果，我们比如查看上面的第三个解，可以发现，树A经过置换只能转变成B,C,H,J,L之一，也就是在6棵树{A,B,C,H,J,L}会相互置换，显然是一个6阶置换群$S_6$的一个12阶子群。同样树{D,E,F,G,I,K}同时相互置换。{M,Q,R,S}相互置，{N,P,O,T}相互置换。于是20棵树被拆分成6+6+4+4的小组，每个小组内进行置换，那么不同小组内的树之间的置换关系必然有着密切的联系：
比如两种置换关系可以同构的，或者一个是另外一个的正规子群。
比如链接 https://groupprops.subwiki.org/w ... _groups_of_order_12 中给出了12阶群的结构, 比如上面第三个解的置换群应该同构于$A_4$

mathe

但是并不是所有的最优解都具有明显的对称性，比如19棵树的部分最优解:
ACKLBCENCFQRLNPSBDKMJMNRHMOSGMPQFKNOJLOQDOPREKQSAIRSFILMDHNQGHLRIJKPEGIODGJSEFHP
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
        [+1*t^2+1/2*t+1/4](复数解)
        -1*v10-1*t
        +1*v0+2*v10-1
        +1*v4+1*v10-1
        +1*v3-2*v10
        +1*v5+2*v10-2
        +1*v7+2*v10-1
        +1*v8+2*v10-1
        +1*v9-1*v10-1/2
        +1*v11-1/2
        +1*v1-2*v10+1
        +1*v2-2/3*v10-1/3
        +1*v6+4/3*v10-1/3
        A[+1,v0,0];
        B(v6,v2)
        C[+1,v1,0];
        D(v7,v2)
        E(v8,v3)
        F(+1,+0)
        G(v4,v9)
        H(v4,v10)
        I(+1,+1)
        J(v5,+1)
        K[+1,+0,0];
        L[+0,+1,0];
        M(+1,v2)
        N(+0,+0)
        O(v5,+0)
        P(+0,+1)
        Q(v5,v3)
        R(v4,v11)
        S(+0,v3)

ACKLBCENCIRSLMQRBDKMHMNSFMOPGKNQJNPRDLNOEKORDPQSAGOSFJLSHIKPHJOQEGLPGIJMEFIQDFHR
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
        +1*v7*v9-1*v9-1/2*v11+1/2
        +1*v2-3*v9
        +1*v4+1*v11-1
        +1*v1+12*v9+6*v11-5
        +1*v3-6*v9-4*v11+3
        +1*v0*v9-4*v9-2*v11+2
        +1*v9*v10-3/2*v9-1/2*v11+1/2
        +1*v0*v11-1*v0+6*v9+2*v11-2
        +1*v7*v11-1*v7+3/2*v9+1/2*v11-1/2
        +1*v9*v11-1/2*v9
        +1*v10*v11+3/2*v9-1*v10
        +1*v11^2-3/2*v11+1/2（v11=1/2）
        +1*v5-3/2*v9
        +1*v6-2*v9-2*v11+1
        +1*v8-3*v9-1*v11+1
        +1*v9^2-1/2*v9-1/6*v11+1/6 (v9^2 - 1/2*v9 + 1/12=0,复数解）
        A[+1,v0,0];
        B(+1,+0)
        C[+1,v1,0];
        D(v2,+0)
        E(v4,v3)
        F(v5,v7)
        G(v4,+1)
        H(v8,v6)
        I(v9,v6)
        J(v5,v10)
        K[+1,+0,0];
        L[+0,+1,0];
        M(+0,+0)
        N(v2,+1)
        O(v2,v3)
        P(v4,v6)
        Q(+0,+1)
        R(+0,v3)
        S(v5,v11)


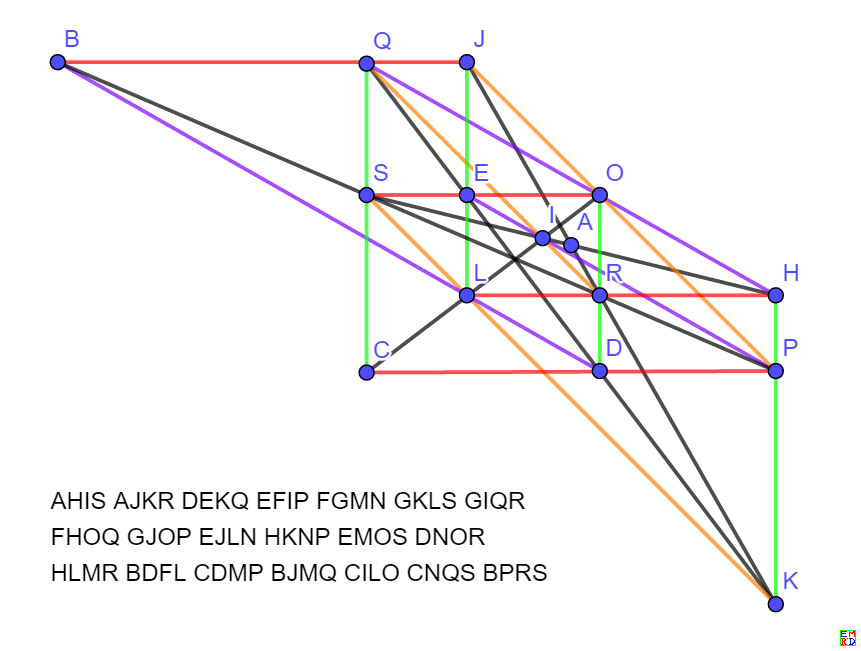
AHISAJKRDEKQEFIPFGMNGKLSGIQRFHOQGJOPEJLNHKNPEMOSDNORHLMRBDFLCDMPBJMQCILOCNQSBPRS
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
        [+1*t^3+3*t^2+2*t-1]
        -1*v11-1*t^2-3*t-2
        -1*v10-1*t
        +1*v1+1
        +1*v0-2*v10+1*v11+3
        +1*v2-1*v10+1
        +1*v3+1*v10-1*v11-2
        +1*v4+1*v10-1*v11-2
        +1*v5+1*v10-2
        +1*v9+2*v10-1*v11-3
        +1*v6+1*v10-1/2*v11-2
        +1*v7+1/2*v10-1/2*v11-1
        +1*v8-1*v11
        A(v6,v7)
        B(v8,+1)
        C(v3,v2)
        D(+1,v2)
        E(+0,+0)
        F[+1,v0,0];
        G[+1,v1,0];
        H(v5,v4)
        I(v9,v10)
        J(+0,+1)
        K(v5,v11)
        L(+0,v4)
        M[+1,+0,0];
        N[+0,+1,0];
        O(+1,+0)
        P(v5,v2)
        Q(v3,+1)
        R(+1,v4)
        S(v3,+0)


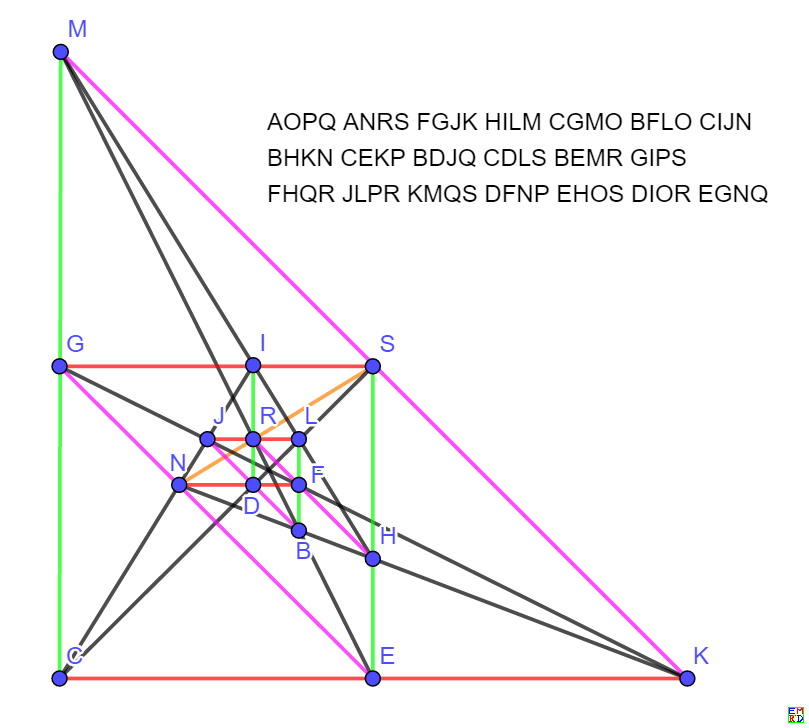
AOPQANRSFGJKHILMCGMOBFLOCIJNBHKNCEKPBDJQCDLSBEMRGIPSFHQRJLPRKMQSDFNPEHOSDIOREGNQ
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
ACBDEIHGFLMJKONRSPQ 01 00 03 02 07 06 05 04 11 10 09 08 13 12 14 15 18 19 16 17
ACBEDGFIHKJMLNOQPSR 00 01 02 03 05 04 07 06 09 08 11 10 13 12 15 14 19 18 17 16
ABCEDHIFGMLKJONSRQP 01 00 03 02 06 07 04 05 10 11 08 09 12 13 15 14 17 16 19 18
        [+1*t^2+3*t+1]
        -1*v11-1*t
        +1*v2-2*v11
        +1*v3+1*v11-1
        +1*v1+1
        +1*v10-2
        +1*v4+1*v11-1
        +1*v5-2*v11
        +1*v6+4*v11-2
        +1*v7-1*v11
        +1*v8+4*v11-2
        +1*v9-2
        +1*v0+1*v11-1
        A[+1,v0,0];
        B(v2,v6)
        C(+0,+0)
        D(v4,v3)
        E(+1,+0)
        F(v2,v3)
        G(+0,+1)
        H(+1,v7)
        I(v4,+1)
        J(v8,v5)
        K(v9,+0)
        L(v2,v5)
        M(+0,v10)
        N(v11,v3)
        O[+0,+1,0];
        P[+1,+0,0];
        Q[+1,v1,0];
        R(v4,v5)
        S(+1,+1)

去除无穷远点得



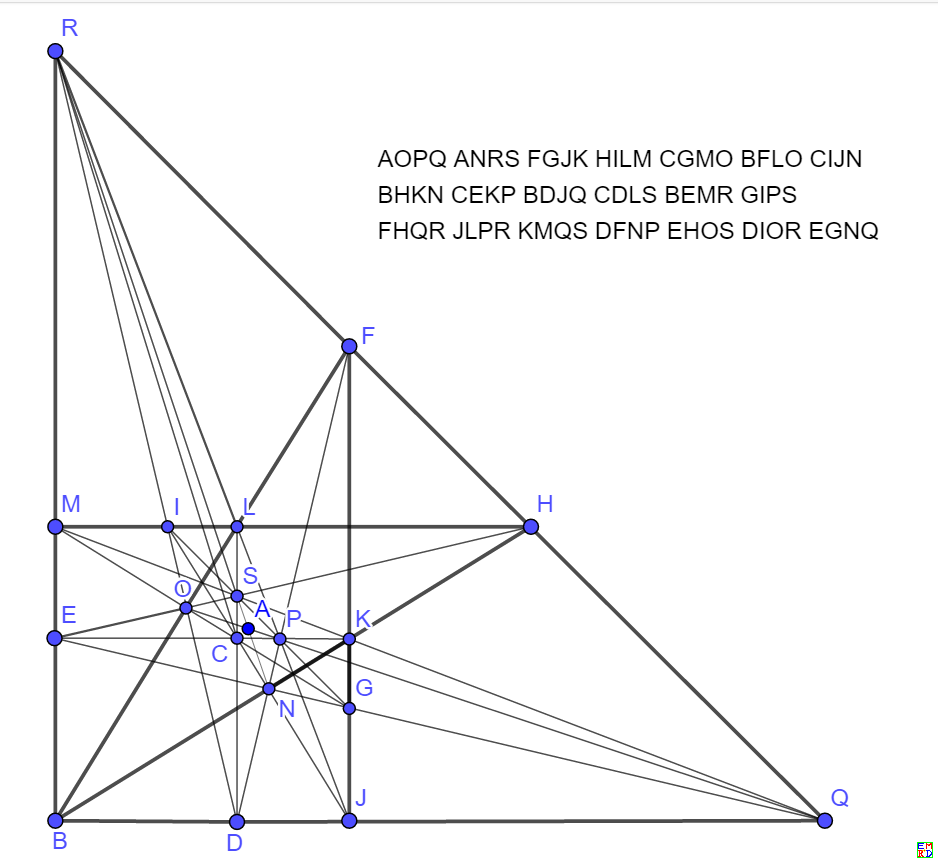
AOPQANRSHIJMGKLMCFMRDEMSFJLNBEKNBFHOEGIODFGQBCGPCINQDHNPCKOSDLORBJQSHKQRILPSEJPR
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
        [+1*t^2+1*t+1/3](复数解）
        -1*v11-1*t
        +1*v1+3/2*v11
        +1*v2-1/2
        +1*v3+1*v11-1
        +1*v5-3/2*v11
        +1*v6-3*v11+1
        +1*v4+2*v11-2
        +1*v7-2*v11
        +1*v8+3/2*v11-3/2
        +1*v0-3*v11+3/2
        +1*v9+6/7*v11-8/7
        +1*v10-3/7*v11-3/7
        A[+1,v0,0];
        B(+0,+1)
        C(v3,v2)
        D(+1,+0)
        E(v4,v6)
        F(+0,+0)
        G(v4,+0)
        H(+0,v5)
        I(v4,v2)
        J(v7,+1)
        K(v3,v5)
        L(+1,v8)
        M(v9,v10)
        N(v11,v2)
        O[+0,+1,0];
        P[+1,v1,0];
        Q[+1,+0,0];
        R(+1,v5)
        S(v3,+1)

BCDEBIOSBHNRAHJSGIKRFGHMEFJNEGLOHLPQJKMPKLNSAKOQCGPSCJQRDFQSDLMREIMQDINPFOPRCMNO
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
        [+1*t^3+1*t^2+2*t+1]
        A(+0,+0)
        B[+1,t^2-t-1,0];
        C(-t^2-t-2,t^2-t)
        D(2*t^2+t+3,-t^2-3*t-1)
        E(t^2,1-t^2)
        F(2*t^2+t+3,1-t)
        G(-t^2-t-2,1-t^2)
        H(+0,+1)
        I[+1,t^2+t,0];
        J(+0,-t)
        K(+1,+0)
        L(+1,1-t^2)
        M(t,t^2-t)
        N(+1,t^2-t)
        O[+1,+0,0];
        P(-t^2-t-2,1-t)
        Q(2*t^2+t+3,+0)
        R(-3*t^2 - t - 5,1-t)
        S[+0,+1,0];



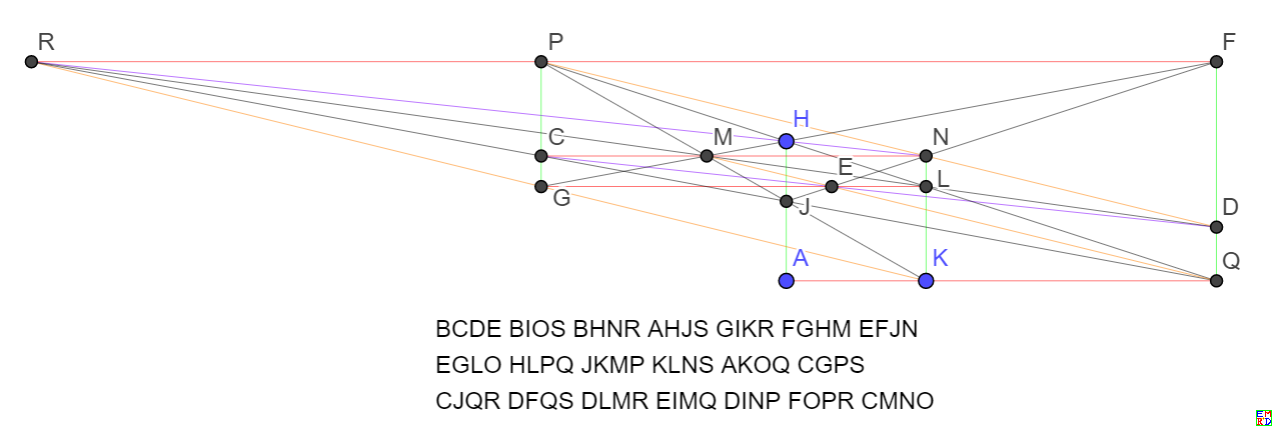
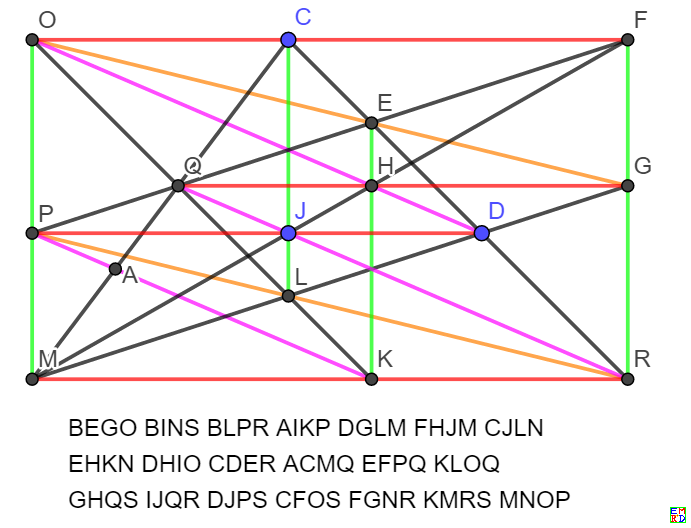
BEGOBINSBLPRAIKPDGLMFHJMCJLNEHKNDHIOCDERACMQEFPQKLOQGHQSIJQRDJPSCFOSFGNRKMRSMNOP
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
        [+1*t^3+3*t^2+2*t-1]
        A(t^2-1,-2*t^2-3*t+1)
        B[+1,t^2+2*t-1,0];
        C(+0,+1)
        D(+1,+0)
        E(t^2+t,-t^2-t+1)
        F((t+1)^2,+1)
        G((t+1)^2,-t^2-2*t+1)
        H(t^2+t,-t^2-2*t+1)
        I[+1,-t^2-t,0];
        J(+0,+0)
        K(t^2+t,-t^2-2*t)
        L(+0,-t)
        M(-t-1,-t^2-2*t)
        N[+0,+1,0];
        O(-t-1,+1)
        P(-t-1,+0)
        Q(t^2+t-1,-t^2-2*t+1)
        R((t+1)^2,-t^2-2*t)
        S[+1,+0,0];


CDEFFIJRFHKSGJPSGKQRCJNQCKOPDHOREINSGHIMEJMODKMNDILQEHLPGLNOFMPQCLRSBOQSANPRABLM
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
BACEDFGIHKJLMONQPSR 00 02 01 04 03 06 05 08 07 09 11 10 13 12 14 15 16 18 17 19
        [+1*t^2+2*t+4]（复数解）
        A(1/2*t+1,-2/3*t-2/3)
        B(t/4+1/2,-t/2)
        C(+0,+0)
        D(t/4+1/2,-t/4)
        E(+1,-1-t/2)
        F(t/2,+1)
        G[+1,t/2,0];
        H(+1,+1)
        I(t+2,-1-t/2)
        J[+1,v1,0];
        K(+0,+1)
        L(+1,+0)
        M(t/2,-t)
        N(1/2*t+1,-1-t/2)
        O(+0,-t/2)
        P[+0,+1,0];
        Q(t/2,-t/2)
        R(1/2*t+1,+0)
        S[+1,+0,0];


CFGNCHIODGKQEFJPDIJREHKSJKNOGIPSFHQRFIKLGHJMDLNPEMNQCLQSCMPRDMOSELORBNRSAOPQABLM
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
BAECDJFKHIGMLPSRNOQ 03 05 00 04 01 02 07 08 06 10 09 14 11 12 16 13 15 18 17 19
BACDEHIFGKJMLONSRQP 01 00 04 05 02 03 06 07 08 10 09 15 16 14 13 11 12 18 17 19
ABDECIJGKHFLMRQOPSN 04 02 03 01 05 00 08 06 07 09 10 16 14 11 15 12 13 17 18 19
ABECDKHJFGILMSPQONR 05 03 01 02 00 04 07 08 06 09 10 13 15 16 12 14 11 17 18 19
BADCEKGJIHFLMQRSNOP 02 04 00 05 01 03 08 07 06 09 10 13 12 11 15 14 16 18 17 19
ABCEDGFIHKJMLNOQPSR 00 01 03 02 05 04 06 08 07 10 09 12 11 14 13 16 15 17 18 19
BAEDCFJHKGILMPSNRQO 03 05 04 00 02 01 07 06 08 09 10 11 14 16 12 15 13 18 17 19
BACEDIHGFJKLMONRSPQ 01 00 05 04 03 02 06 08 07 09 10 16 15 13 14 12 11 18 17 19
ABDCEJIKGFHMLRQPONS 04 02 01 03 00 05 08 07 06 10 09 14 16 15 11 13 12 17 18 19
ABEDCHKFJIGMLSPOQRN 05 03 02 01 04 00 07 06 08 10 09 15 13 12 16 11 14 17 18 19
BADECGKIJFHMLQRNSPO 02 04 05 00 03 01 08 06 07 10 09 12 13 15 11 16 14 18 17 19
        Parameter [+1/3+1*t^2=0]（复数解）
        A[+1/2+3/2*t ,+1/2-3/2*t , +1]
        B[+1/2-3/2*t ,+1/2+3/2*t , +1]
        C[+1/2-1/2*t ,+1/2-1/2*t , +1]
        D[0 ,0 , +1]
        E[+1 ,+1 , +1]
        F[+1/2-1/2*t ,+1-1*t , +1]
        G[+1/2-1/2*t ,-1*t , +1]
        H[+1-1*t ,+1/2-1/2*t , +1]
        I[-1*t ,+1/2-1/2*t , +1]
        J[+1 ,+1/2+3/2*t , 0]
        K[+1 ,+1/2-3/2*t , 0]
        L[0 ,+1 , +1]
        M[+1 ,0 , +1]
        N[0 ,+1 , 0]
        O[+1 ,0 , 0]
        P[0 ,+1/2-3/2*t , +1]
        Q[+1 ,+1/2-3/2*t , +1]
        R[+1/2-3/2*t ,+1 , +1]
        S[+1/2-3/2*t ,0 , +1]


DEFSGILSHJKSDIKRDJLQEGJOEHIPFGKMFHLNMPQSNORSADMNAFOPAEQRBJPRCIOQCLMRBKNQCGNPBHMO
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
ACBEFDKLHGIJRQMNOPS 00 02 01 06 05 07 08 03 04 10 09 13 11 12 18 19 14 15 17 16
ABCFDEIJLKHGPORQMNS 00 01 02 08 07 03 04 06 05 09 10 12 13 11 17 16 18 19 15 14
ACBDEFHGJILKNMPORQS 00 02 01 04 03 06 05 08 07 10 09 11 12 13 15 14 17 16 19 18
ABCEFDLKGHJIQRNMPOS 00 01 02 05 06 08 07 04 03 09 10 13 11 12 19 18 15 14 16 17
ACBFDEJIKLGHOPQRNMS 00 02 01 07 08 04 03 05 06 10 09 12 13 11 16 17 19 18 14 15
        +1*v0+1
        +1*v1-1*v8
        +1*v2+1*v8
        +1*v3+1*v8+1*v10+1*v11-2
        +1*v4-1*v8-1*v10-1*v11+1
        +1*v5+1*v8+1*v10+1*v11-1
        +1*v6+1*v8+1*v11
        +1*v7+1*v8+1
        +1*v9-1*v10+1
        +1*v8^2+1*v8+1（复数解）
        +1*v8*v10-2*v8-1*v11
        +1*v10^2+1*v8-1*v10+1*v11-1
        +1*v8*v11+1*v10+1*v11-2
        +1*v10*v11-1*v10+1
        +1*v11^2-1*v8-2*v10-3*v11+4
        A(+1,+0)
        B(v7,+1)
        C(v8,v2)
        D(v3,+0)
        E(v3,v9)
        F(v3,v4)
        G(v5,v4)
        H(v6,+1)
        I(v5,v10)
        J(v6,v11)
        K(v6,v4)
        L(v5,v2)
        M[+1,+0,0];
        N(+0,+0)
        O(+0,+1)
        P[+1,v0,0];
        Q[+1,v1,0];
        R(+0,v2)
        S[+0,+1,0];

DGIPEFHQCFLOCGKNDHLNEIKOFGRSCHPSCIQRDMOREMNSDJQSEJPRNOPQBGJOAFJNBILSAHKRALMQBKMP
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
BACEDGFIHJLKMONQPSR 01 00 03 02 05 04 06 08 07 10 09 12 11 13 15 14 17 16 19 18
        A[+4 ,+1 , +1]
        B[+1 ,+4 , +1]
        C[0 ,0 , +1]
        D[+2 ,-2 , +1]
        E[-2 ,+2 , +1]
        F[+1 ,-1/2 , 0]
        G[+1 ,-2 , 0]
        H[0 ,+1 , +1]
        I[+1 ,0 , +1]
        J[+2 ,+2 , +1]
        K[-1/2 ,+1 , +1]
        L[+1 ,-1/2 , +1]
        M[-2 ,-2 , +1]
        N[-2 ,+4 , +1]
        O[+4 ,-2 , +1]
        P[0 ,+2 , +1]
        Q[+2 ,0 , +1]
        R[+1 ,0 , 0]
        S[0 ,+1 , 0]

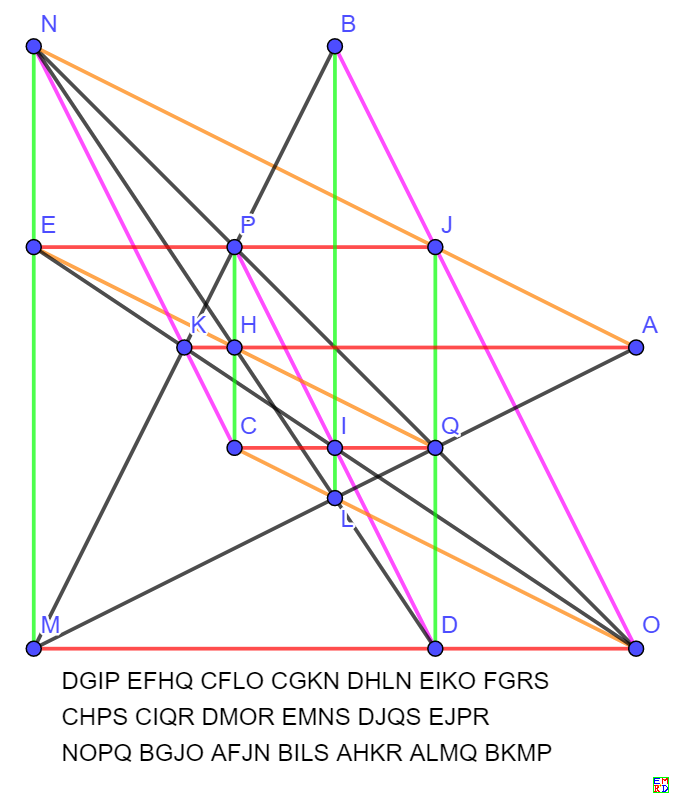
去除无穷远点，得到


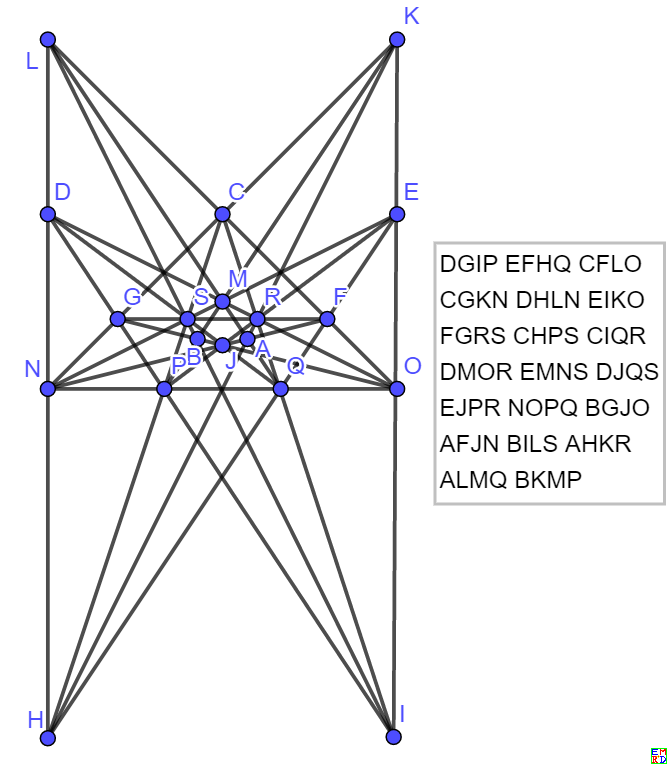
DIKQEIJPFHKRGHJSCFPSCGQRCINOEKOSDJNRCJKMDEHLEFMNDGMOHMPQILRSFLOQGLNPBNQSAOPRABLM
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
BACEDGFHIKJLMONQPSR 01 00 03 02 05 04 06 08 07 09 10 12 11 13 14 16 15 18 17 19
        +1*v3+1*v10
        +1*v5+1*v10+1
        +1*v10*v11-2*v8+1*v11
        +1*v4-2*v8
        +1*v8*v10+1/2*v11
        +1*v8^2-1/2*v8+1/2*v11-3/4
        +1*v10^2+1*v10+1（复数解）
        +1*v1+2/3*v8-2/3*v11+1
        +1*v2-2/3*v8-1/3*v11
        +1*v6-4/3*v8+1/3*v11
        +1*v9+1/2*v10
        +1*v8*v11-2*v8+3/2*v10+1/2*v11
        +1*v0-2/3*v8+1*v10-1/3*v11+1
        +1*v7-1/3*v8+1/2*v10+1/3*v11
        +1*v11^2-2*v8+3*v10-1*v11+3
        A(+1,+0)
        B(v2,v7)
        C[+1,v0,0];
        D(v8,v9)
        E(+0,+1)
        F[+1,v1,0];
        G(v4,v3)
        H(v4,v5)
        I(v6,+1)
        J(v4,+1)
        K(+0,v10)
        L(v6,v3)
        M(v11,v5)
        N(v2,v3)
        O(+0,+0)
        P[+1,+0,0];
        Q(v2,v5)
        R(v6,+0)
        S[+0,+1,0];


FIKNEJLNDHIPDGJOEHKOFGLPDEFMIJMQGKMRHLMSFOQSEPQRDNRSMNOPCGHQBJKSAILRABNQACPSBCOR
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
BCAFDELIKGHJMOPNRSQ 04 03 00 05 02 01 06 08 09 07 11 12 10 13 16 14 15 19 17 18
CABEFDJKHLIGMPNOSQR 02 05 04 01 00 03 06 09 07 08 12 10 11 13 15 16 14 18 19 17
BACDFEHGJILKMNPOQSR 01 00 03 02 05 04 06 07 09 08 11 10 12 13 14 16 15 17 19 18
CBAFEDILGKJHMONPRQS 03 04 05 00 01 02 06 08 07 09 12 11 10 13 16 15 14 19 18 17
ACBEDFKJLHGIMPONSRQ 05 02 01 04 03 00 06 09 08 07 10 12 11 13 15 14 16 18 17 19
        Parameter [+1+1*t+1*t^2=0]（复数解）
        A[-1-2*t ,-1-2*t , +1]
        B[-1 ,-1-2*t , +1]
        C[-1/3-2/3*t ,+1 , +1]
        D[+1 ,+2+1*t , +1]
        E[+1 ,0 , +1]
        F[+1 ,+1-1*t , +1]
        G[0 ,+1 , +1]
        H[-1*t ,+1 , +1]
        I[+1 ,+1 , 0]
        J[+1 ,+1+1*t , 0]
        K[0 ,-1*t , +1]
        L[-1*t ,-1*t , +1]
        M[0 ,+1 , 0]
        N[-1-1*t ,-1-2*t , +1]
        O[-1-1*t ,+1-1*t , +1]
        P[-1-1*t ,0 , +1]
        Q[+1 ,0 , 0]
        R[0 ,0 , +1]
        S[-1*t ,+1-1*t , +1]


JNQSJOPRIJLMFKRSIKPQGHJKFHOQFGNPGIOSHINREGLREHMSDLPSDMQRDENOCEFJAKLNBKMOBCLQACMP
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
BACDEFHGIJKMLONQPSR 01 00 02 03 04 05 07 06 09 08 11 10 13 12 14 15 17 16 19 18
        Parameter [+1-1*t+1*t^2=0]（复数解）
        A[+1/2*t ,-1/2+1/2*t , +1]
        B[+2*t ,-1 , +1]
        C[+1 ,-2+2*t , +1]
        D[-1*t ,+1*t , +1]
        E[+1 ,+1-1*t , +1]
        F[+1 ,0 , +1]
        G[+1*t ,+1 , +1]
        H[+1*t ,+1-1*t , +1]
        I[-1+1*t ,+1 , +1]
        J[0 ,+1 , 0]
        K[+1*t ,0 , +1]
        L[-1+1*t ,+1*t , +1]
        M[-1+1*t ,+1-1*t , +1]
        N[+1 ,-1*t , 0]
        O[0 ,+1 , +1]
        P[0 ,+1*t , +1]
        Q[+1 ,-1 , 0]
        R[0 ,0 , +1]
        S[+1 ,0 , 0]


JNRSJOPQGHIJJKLMAINOCGPSBHQRCLNQAKPRBMOSFMNPFKQSFLORDGKNEHKOEGMQEILPDHLSDIMRABCJ
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
CBAEDFIHGJLKMPSNRQO 01 00 02 03 05 04 06 08 07 09 10 12 11 16 17 18 13 14 15 19
ACBEDFHGIJKMLONRSPQ 01 00 02 03 04 06 05 09 08 07 12 11 10 14 13 17 18 15 16 19
BCADEFIGHJMKLRQOPSN 00 01 02 03 06 04 05 08 09 07 12 10 11 18 15 16 14 13 17 19
CABDEFHIGJLMKSPQONR 00 01 02 03 05 06 04 09 07 08 11 12 10 17 16 14 15 18 13 19
BACEDFGIHJMLKQRSNOP 01 00 02 03 06 05 04 07 09 08 11 10 12 15 18 13 17 16 14 19
        Parameter [+3+1*t^2=0]（复数解）
        A[+1 ,0 , +1]
        B[+1 ,-1/2-1/2*t , +1]
        C[+1 ,+1/2-1/2*t , +1]
        D[-1+1*t ,+3/2-1/2*t , +1]
        E[-1/4+1/4*t ,+3/4-1/4*t , +1]
        F[-1 ,+1 , +1]
        G[+1/2+1/2*t ,+3/2-1/2*t , +1]
        H[+1/2+1/2*t ,-1*t , +1]
        I[+1/2+1/2*t ,0 , +1]
        J[0 ,+1 , 0]
        K[-1/2+1/2*t ,+3/2-1/2*t , +1]
        L[-1/2+1/2*t ,+1/2-1/2*t , +1]
        M[-1/2+1/2*t ,+1 , +1]
        N[+1 ,0 , 0]
        O[0 ,0 , +1]
        P[0 ,+1 , +1]
        Q[0 ,+1/2-1/2*t , +1]
        R[+1 ,-1 , 0]
        S[+1 ,-1/2-1/2*t , 0]

那些置换关系只有一种的显然是不具有任何对称性的，至少现在已知很多较好的解（比如大部分已知的21棵树以上当前最佳的整数坐标解都不具有明显的对称性）。
另外从搜索的复杂度来说，对称性越强，我们可以一次性处理越多的行，代码搜索效率越高。现在处理20多棵树，如果置换群的阶不小于3，计算机基本上还是可以穷举的。但是置换群小于等于2（比如左右对称的情况），就已经很难穷举了。这也是为什么我最近找出来的结果会具有高度对称性。
但是另外一个比较麻烦的现象是我发现满足高度对称性的大部分解都是复数解，没有实数解。

wayne

wayne 发表于 2019-12-15 13:21
我刚才查了下.发现是我疏忽了. 方程组解出来有三组解,第一个解是增根, 应该剔除. 我试了下第二组,第三组, ...

直接在 原贴 更新 了. 关于前面两次 计算没有结果的情况.

106#出现了四边形,跟 107#的四边形在细节上不一样,边上的点的度都是6,107楼是5..
另外, 107#的另一个解不存在 实数解.

sheng_jianguo

mathe 发表于 2019-12-16 08:31
但是并不是所有的最优解都具有明显的对称性，比如19棵树的部分最优解:
ACKLBCENCFQRLNPSBDKMJMNRHMOSGMPQF ...

分析的非常好！
请教mathe，这里的19棵树的“部分”最优解是否只是19棵树的最优解中的一部分解？19棵树的最优解（20行）一共有多少（不止这里的15个）？

mathe

sheng_jianguo 发表于 2019-12-16 20:10
分析的非常好！
请教mathe，这里的19棵树的“部分”最优解是否只是19棵树的最优解中的一部分解？19棵树 ...

19棵树20行也应该挺多的，只是我没有全部搜索。理论上这个计算量不会超过排除20棵树不存在24行的解的计算量，只是那次计算没有记录19棵树的结果。

数学星空

对于100#的结果，我试着按照mathe的方案做了一下：

首先根据100#的方程得到：

\({v0 = 0.307978528369904, v1 = 0.19806226419516, v10 = 0.307978528369904, v11 = -2.80193773580484, v12 = 9.0978346790447, v13 = -3.49395920743493, v14 = 2.80193773580484, v15 = -4.04891733952231, v16 = -1.24697960371747, v17 = 14.1467520185669, v2 = -2.24697960371747, v3 = -1.80193773580484, v4 = -0.55495813208737, v5 = -6.29589694323978, v6 = -11.3448142827620, v7 = 2.24697960371747, v8 = 5.04891733952230, v9 = -0.80193773580484}\)

然后删除带有z值的四个点\(A[1, 0.307978528369904, 0]，J[1, 0.19806226419516, 0]，P[1, 0, 0]，W[0, 1, 0]\)

画出其余点的图形得到：



然后观察发现\(S,Q,U,X\)可以构成矩形四个点，因此我们设法构造射影变换[[a1,a2,a3],[b1,b2,b3],[c1,c2,c3]]

不妨设S[-11.3448142827620,-1.80193773580484,1]->[-1,1,1],Q[-11.3448142827620,-4.04891733952231,1]->[-1,-1,1],U[14.1467520185669,2.24697960371747,1]->[1,-1,1]

由[-11.3448142827620,-1.80193773580484,1]，[-11.3448142827620,-4.04891733952231,1]，[14.1467520185669,2.24697960371747,1]]*[[a1,a2,a3],[b1,b2,b3],[c1,c2,c3]]=[[-1,1,1],[-1,-1,1],[1,-1,1]]

解得：{a1 = 0.07845732100, a2 = -0.2198325283, a3 = 0., b1 = 0., b2 = 0.8900837358, b3 = 0., c1 = -0.1099162642, c2 = 0.1099162642, c3 = 1.}

然后将所有点经过射影变换得到：

1, A[0.0784573210000000, 0.0542941507776705, 0.],
2, B[-0.286208264249314, -0.109916264240422, 1.],
3, C[-0.286208264249314, -1.00000000004042, 1.],
4, D[-0.0314589432000000, -0.109916264100000, 1.],
5, E[-0.109916264200000, 1., 1.],
6, F[-0.603875471658682, 0.999999999727726, 1.],
7, G[-0.109916264200000, 0.384042943277670, 1.],
8, H[-1.00000000006804, 0.109916263709357, 1.],
9, I[0.603875471618742, 0.109916264593434, 1.],
10,J[0.0784573210000000, -0.0435405282641654, 0.],
11,K[0.286208264209367, -0.999999999724897, 1.],
12,L[-0.384042943298628, 0.384042943126569, 1.],
13,M[0.109916264160054, 0.384042943398845, 1.],
14,N[-0.603875471658682, -0.109916264415523, 1.],
15,O[-0.286208264249314, 0.109916264102827, 1.],
16,P[0.0784573210000000, -0.219832528300000, 0.],
17,Q[-1.00000000006804, -1.00000000043389, 1.],
18,R[-0.603875471658682, 0.384042943005393, 1.],
19,S[-1.00000000006804, 0.999999999509356, 1.],
20,T[-0.109916264200000, 0.109916264200000, 1.],
21,U[1.00000000002810, -0.999999999331441, 1.],
22,V[0.286208264209367, -0.109916263924897, 1.],
23,W[0., 0.890083735800000, 0.],
24,X[0.286208264209367, 1.00000000021835, 1.]

好像还是存在上面四个无穷远点

\(A[0.0784573210000000, 0.0542941507776705, 0.]，J[0.0784573210000000, -0.0435405282641654, 0.]，P[0.0784573210000000, -0.219832528300000, 0.]，W[0., 0.890083735800000, 0.]\)

然后作图得到：


感觉还是有点乱~~~

mathe

如果把矩形还是映射为矩形，不会改变无穷远直线。

mathe

Q=[-11.34481428,-4.0489173,1];
V=[5.04891734,1,1];
U=[14.146752,2.2469796,1];
N=[-6.2958969,-1.8019377,1];
T=matrix(12,13);
for(u=1,3, T[1,u]=Q[u]); T[1,10]=1;
for(u=1,3,T[2,u+3]=Q[u]); T[2,10]=-1;
for(u=1,3,T[3,u+6]=Q[u]); T[3,10]=-1;
for(u=1,3, T[4,u]=V[u]); T[4,11]=1;
for(u=1,3,T[5,u+3]=V[u]); T[5,11]=1;
for(u=1,3,T[6,u+6]=V[u]); T[6,11]=-1;
for(u=1,3, T[7,u]=U[u]); T[7,12]=-1;
for(u=1,3,T[8,u+3]=U[u]); T[8,12]=1;
for(u=1,3,T[9,u+6]=U[u]); T[9,12]=-1;
for(u=1,3, T[10,u]=N[u]); T[10,13]=-1;
for(u=1,3,T[11,u+3]=N[u]); T[11,13]=-1;
for(u=1,3,T[12,u+6]=N[u]); T[12,13]=-1;
R=matker(T)~[1,1..9];
S=matrix(3,3);
for(u=1,3,S[1,u]=R[u];S[2,u]=R[u+3];S[3,u]=R[u+6])
Q1=S*Q~;Q1=Q1/Q1[3]
V1=S*V~;V1=V1/V1[3]
U1=S*U~;U1=U1/U1[3]
N1=S*N~;N1=N1/N1[3]
S
(17:32) gp > Q1=S*Q~;Q1=Q1/Q1[3]
%27 = [-0.99999999999999999999999999999999999999, 1.0000000000000000000000000000000000000, 1.0000000000000000000000000000000000000]~
(17:33) gp > V1=S*V~;V1=V1/V1[3]
%28 = [-0.99999999999999999999999999999999999998, -1.0000000000000000000000000000000000000, 1.0000000000000000000000000000000000000]~
(17:33) gp > U1=S*U~;U1=U1/U1[3]
%29 = [1.0000000000000000000000000000000000001, -1.0000000000000000000000000000000000000, 1.0000000000000000000000000000000000000]~
(17:33) gp > N1=S*N~;N1=N1/N1[3]
%30 = [1.0000000000000000000000000000000000000, 1.0000000000000000000000000000000000000, 1.0000000000000000000000000000000000000]~
(17:33) gp > S
%31 =
[-0.80193773756270369940242713202277356305 3.2469796371098373233407689072419403976 1.8019377033264951371085486079689846186]

[0.30797853004745113481824003627020087146 -1.2469796247221924651414889934781979754 0.69202147567353382300925465632602616902]

[-0.088145996857696001725075676626895484682 -0.35689588362562221183310122454908088683 -0.19806225604359934786274980917182808898]

数学星空

根据mathe的计算思路：

我求得射影变换为A=[[-0.4450418679,1.801937736,1],[0.4450418679,-1.801937736,1],[0.4450418679,1.801937736,1]]

mathe的计算结果：B=[[-0.8019377376, 3.246979637, 1.801937703], [0.3079785300, -1.246979625, 0.6920214757], [-0.08814599686, -0.3568958836, -0.1980622560]]
若将B的第三个坐标Z归一为1，即
[[-0.8019377376/1.801937703, 3.246979637/1.801937703, 1.801937703/1.801937703], [0.3079785300/0.6920214757, -1.246979625/0.6920214757, 0.6920214757/0.6920214757], [-0.08814599686/-0.1980622560, -0.3568958836/-0.1980622560, -0.1980622560/-0.1980622560]]=[[-0.4450418679,1.801937736,1],[0.4450418679,-1.801937736,1],[0.4450418679,1.801937736,1]]

通过A矩阵可以得到：

[-0.235461455735814, 0.953363971048208, A],
[-0.531083406343389, 0.391395846197808, B],
[-0.210928687292749, -0.327985277641204, C],
[0., 1.80193773600000, D],
[0.445041867900000, 0., E],
[-0.512745566466989, 1.46010735830862, F],
[0.445041867900000, 0.953363971048208, G],
[-0.323044018598587, 1.03385184939642, H],
[-0.210928687292751, 1.14596718071759, I],
[-0.297894256874738, 1.20614922216910, J],
[-0.297894256874736, 1.80193773600000, K],
[-0.574964881306834, 1.14596718071759, L],
[-0.0743233018664421, 1.05143332084936, M],
[-0.344477150906585, 0.887016566123953, N],
[-0.664874396243247, 0.692021471705050, O],
[-0.445041867900000, 1.80193773600000, P],
[-0.256502036331518, 0.788177422067996, Q],
[-0.411443109499846, 1.11509011237923, R],
[-0.386277867888054, 1.26731257873887, S],
[0.445041867900000, 1.80193773600000, T],
[-0.278885243289295, 1.33637721938567, U],
[-0.192497060540883, 1.29067121116879, V],
[0.445041867900000, -1.80193773600000, W],
[-0.0966667909773841, 0.825812461623189, X]

画图得到：



与我们想要的结果（111#）有点近似了，但感觉还是有点距离啊~~

射影变换的本质看来还没搞清楚哈~~