果树种植最优解精美图形作法探讨

wayne

我在想,能否 通过 某种变换规则, 使得上面图形的内部 长度比能得到 调整.  这样让点更加分散,而不是现在这样的稍显集中.

wayne

前面也有这种形状的,(见43楼). 但内部 点的布局不一样.



43楼的坐标点全是有理数,而这里的坐标全是 无理数
ABCDEFGHIJKLMNOPQRST
{{-(9/5)+193/(20 Sqrt[5]),Root[9-9 #1^2+#1^4&,2]},{361/100,0},{1/100 (32+19 Sqrt[5]),Root[9-9 #1^2+#1^4&,1]},{1/100 (206+193 Sqrt[5]),Root[9-9 #1^2+#1^4&,1]},{1/100 (535-174 Sqrt[5]),0},{1/200 (-341+367 Sqrt[5]),-(1/4) Sqrt[3] (-1+Sqrt[5])},{1/200 (-167+193 Sqrt[5]),-(Sqrt[3]/(1+Sqrt[5]))},{1/100 (-316+19 Sqrt[5]),Root[9-9 #1^2+#1^4&,1]},{1/100 (-161+174 Sqrt[5]),0},{13/100,0},{1/100 (-142+193 Sqrt[5]),Root[9-9 #1^2+#1^4&,1]},{1/100 (-702+367 Sqrt[5]),Root[9-9 #1^2+#1^4&,2]},{1/500 (65+38 Sqrt[5]),-Sqrt[(3/5)]},{1/500 (65+734 Sqrt[5]),-Sqrt[(3/5)]},{-(1/4),Sqrt[3]},{1/300 (-309+386 Sqrt[5]),-Sqrt[(5/3)]},{1/100 (-1455+734 Sqrt[5]),Root[9-54 #1^2+#1^4&,2]},{1/100 (-373+348 Sqrt[5]),Sqrt[3]},{1/500 (935+212 Sqrt[5]),-Sqrt[(3/5)]},{7/100 (-23+16 Sqrt[5]),-Sqrt[(3/5)]}}

mathe

好像23行我找到了一个新的图谱
print(BFHICDJKAEGLHJLMDGINAKMNFGKOCIMOEIKPBGMPBCLQFJNQADOQACHRBENRDLPRABJSEHOSCFPSDEFTGHQTIJRTKLST);
solve([+1-2*T_X+1*P_Y*T_X-2*T_X*T_X,+1*P_Y-1*T_X-1*T_X*T_X,+1*P_Y*P_Y+1*T_X-3*P_Y*T_X,+1*N_X-1*P_Y+1*T_X,-1+1*P_X+1*P_Y-1*T_X,-1+1*S_X+1*T_X,-1+1*S_Y-1*T_X,+1*Q_Y+1*T_X,-2+1*A_Y+1*P_Y-1*T_X,+1+1*L_Y-1*P_Y+1*T_X,+3+1*F_Y-1*P_Y+2*T_X,-1+1*N_Y+1*P_Y,-1+1*K_X+1*P_Y,+1*D_X-1*P_Y,-1+1*G_Y+1*P_Y,-1+1*E_X+1*T_X,-1+1*O_X+1*T_X,-1+1*B_Y+1*P_Y-1*T_X,-1+1*R_X,-1+1*A_X,-1+1*D_Y+1*P_Y,+1*G_X-1*T_X,+1*Q_X-1*T_X,-1+1*R_Y,-1+1*T_Y,+1*K_Y-1*P_Y,+1*E_Y-1*P_Y],[P_Y,T_X,N_X,P_X,S_X,S_Y,Q_Y,A_Y,L_Y,F_Y,N_Y,K_X,D_X,G_Y,E_X,O_X,B_Y,R_X,A_X,D_Y,G_X,Q_X,R_Y,T_Y,K_Y,E_Y]);
print("B=(1,B_y,0) C_x=1 C_y=0 F=(1,F_y,0) H=(0,1,0) I=(1,0,0) J_x=0 J_y=1 L_x=0 M_x=0 M_y=0 O_y=0 ");
手工求解发现P_Y应该满足方程
P_Y^3 - 6*P_Y^2 + 5*P_Y - 1=0
取P_Y=0.30797852836990413037218510299793085980,可得如下图（四种彩色直线各自相交于一个无穷远点）

需要注意这个图中过每个点都至少四条直线，和以前的图都不相同

wayne

可惜之前附件的代码下载不了了.

mathe

试着对上面的图做了下变换，去掉无穷远点

mathe

这个三次方程不同的根对应的图应该同构的（前面我少了一条边，结果以为两图不同），比如t=0.64310413210779055610560048997869941660
可以得出如下的图:

通过数值计算各边上四点形成的交比，可以得到三条边上四点的交比为0.198062，0.307979， 0.356896； 其余边上四点的交比均为0.445042，和方程的根的选择无关。

sheng_jianguo

mathe 发表于 2019-9-19 15:35
试着对上面的图做了下变换，去掉无穷远点

@mathe  图形非常漂亮。
由于寻找23行解工作量特大，我想按点和线的关系分类也许搞清23行图的一种方法。任一23行图的点线关系都可以用集合Tdx={<m,n>|n为恰经过m条线的点的个数}来表示，如：{<6,4>,<5,5>,<4,10>,<3,1>}表明此图恰经过6条线的点有4个，恰经过5条线的点有5个，恰经过4条线的点有10个，恰经过3条线的点有1个。
经计算得到：如果23行图每个点至少有4条线相连（所有20棵树其中某一颗树只有不超过3行的所有23行结果已全部求出？），则所有的点线关系集合只可能有以下7个（很有规律）：
1）{<5,12>,<4,8>}，2）{<6,1>,<5,10>,<4,9>}，3）{<6,2>,<5,8>,<4,10>}，4）{<6,3>,<5,6>,<4,11>}，5）{<6,4>,<5,4>,<4,12>}，6）{<6,5>,<5,2>,<4,13>}，7）{<6,6>,<5,0>,<4,14>}
其中第1个就是刚刚找到的23行图，所以只要判别其他6个是否有最优解就可以了（不知这样是否可以减少求所有解的工作量）。

sheng_jianguo

@mathe  谢谢您的点评。由此我的看法如下，有什么不对地方请指正：
关于20棵树（每行4棵）23行有多少种问题是否先认为就是23行最优解（方程）有多少种问题，如果这样认为的话，要知道两点：
1）19棵树（每行4棵）20行一共有多少种解（方程）？从而推出含有经过某棵树只有3行的23行解（方程）的个数。（不可能有经过某棵树只有2行（或少于2行）的23行解，否则19棵树（每行4棵）的最优解是21行（或大于21行），但实际上是20行）
这部分工作已全部完成（从多少种解（方程）得出结果）？推出含有经过某棵树只有3行的23行解（方程）只有2个。
2）18棵树（每行4棵）16行一共有多少种解（方程）？从而推出存在一行，上面至少有两颗树只经过4行的23行解（方程）的个数。（上文78#也证实了：除了情况1）23行只能是这种情况，因为除了情况1）23行树每棵数至少经过4行，则只经过4行的树至少有8棵，意味着这8棵树之间若都没有连线，那么至少要有3*8+1=24棵树，但实际上只有20棵树）
这部分工作没完成（只找到1个解），16行解中，还有多少种没判别？
如果1）和2）都做完了，23行最优解（方程）有多少种问题也就知道了。

mathe

23行最后一部分数据现在计算机大概已经处理了1/3的数据，没有发现新的结果。而这三组数据都重复出现很多次。从概率上来说，继续找到新的解的概率已经不大了。
倒是现在找到了三组21棵树种24行的副产品（网络上能找到21棵树最优结果也是24行），而且都是整数坐标的，
其中第一组中点U还是半自由的（可以沿着一条直线任意滑动），所以从本质上一组代表无穷组

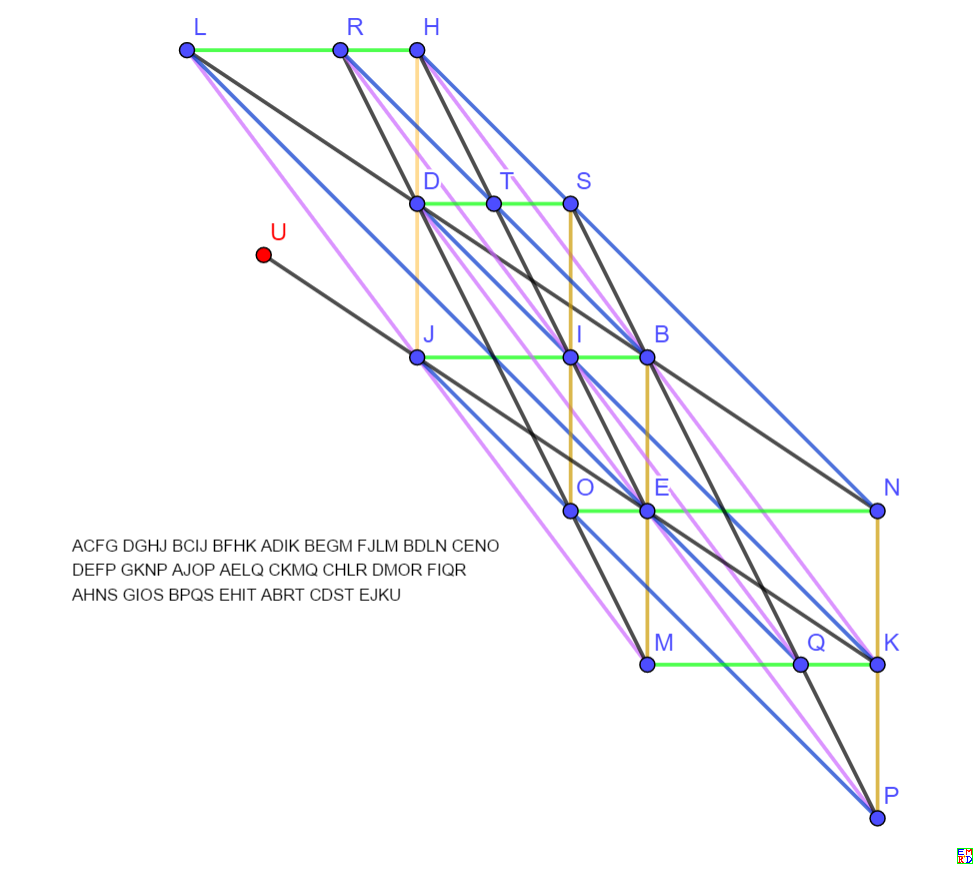
print(ACFGDGHJBCIJBFHKADIKBEGMFJLMBDLNCENODEFPGKNPAJOPAELQCKMQCHLRDMORFIQRAHNSGIOSBPQSEHITABRTCDSTEJKU);
solve([+1*U_X+3/2*U_Y,-1/2+1*T_X,+4/3+1*F_Y,+3+1*P_Y,+2+1*Q_Y,-5/2+1*Q_X,+1/2+1*R_X,+3/2+1*L_X,-3+1*P_X,-2+1*R_Y,+1+1*O_Y,-3/2+1*M_X,+1+1*N_Y,-3/2+1*E_X,-2+1*L_Y,-1+1*O_X,-1+1*S_X,-3+1*N_X,-3+1*K_X,-2+1*H_Y,-3/2+1*B_X,+1+1*A_Y,+2+1*M_Y,-1+1*T_Y,-1+1*S_Y,+1+1*E_Y,+2+1*K_Y],[U_X,T_X,F_Y,P_Y,Q_Y,Q_X,R_X,L_X,P_X,R_Y,O_Y,M_X,N_Y,E_X,L_Y,O_X,S_X,N_X,K_X,H_Y,B_X,A_Y,M_Y,T_Y,S_Y,E_Y,K_Y]);
print("A=(1,A_y,0) B_y=0 C=(1,0,0) D_x=0 D_y=1 F=(1,F_y,0) G=(0,1,0) H_x=0 I_x=1 I_y=0 J_x=0 J_y=0 ");


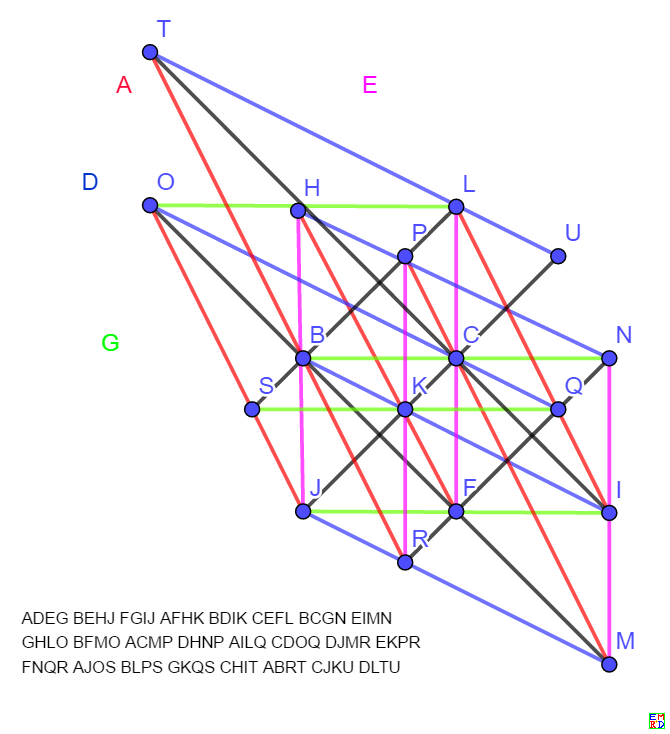
print(ADEGBEHJFGIJAFHKBDIKCEFLBCGNEIMNGHLOBFMOACMPDHNPAILQCDOQDJMREKPRFNQRAJOSBLPSGKQSCHITABRTCJKUDLTU);
solve([-5/6+1*U_Y,-1/3+1*S_Y,+1/6+1*S_X,-3/2+1*T_Y,-5/6+1*P_Y,-1/2+1*N_Y,+1/2+1*M_Y,+1/6+1*R_Y,-5/6+1*Q_X,+1/2+1*O_X,-5/6+1*U_X,-1/3+1*R_X,+2+1*A_Y,-1/2+1*L_X,+1/2+1*D_Y,-1/2+1*B_Y,-1+1*M_X,-1+1*O_Y,-1/3+1*Q_Y,-1/3+1*K_Y,+1/2+1*T_X,-1/2+1*C_Y,-1/2+1*F_X,-1/3+1*P_X,-1/2+1*C_X,-1+1*L_Y,-1+1*N_X,-1/3+1*K_X],[U_Y,S_Y,S_X,T_Y,P_Y,N_Y,M_Y,R_Y,Q_X,O_X,U_X,R_X,A_Y,L_X,D_Y,B_Y,M_X,O_Y,Q_Y,K_Y,T_X,C_Y,F_X,P_X,C_X,L_Y,N_X,K_X]);
print("A=(1,A_y,0) B_x=0 D=(1,D_y,0) E=(0,1,0) F_y=0 G=(1,0,0) H_x=0 H_y=1 I_x=1 I_y=0 J_x=0 J_y=0 ");


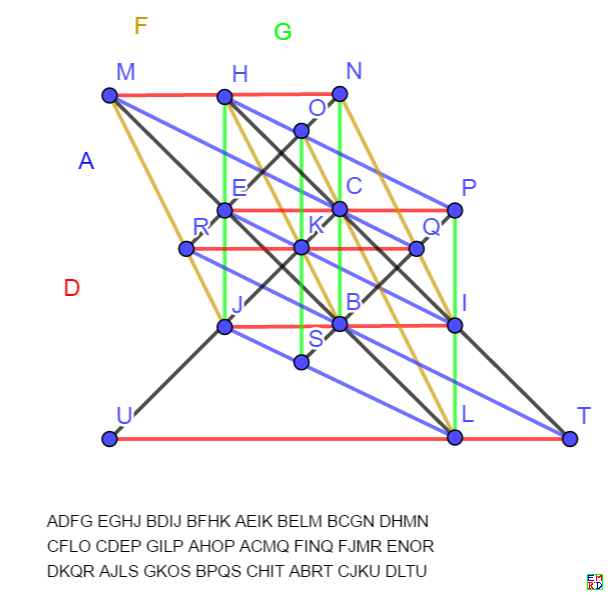
print(ADFGEGHJBDIJBFHKAEIKBELMBCGNDHMNCFLOCDEPGILPAHOPACMQFINQFJMRENORDKQRAJLSGKOSBPQSCHITABRTCJKUDLTU);
solve([-5/6+1*O_Y,+1/2+1*U_X,-1/2+1*P_Y,+1/6+1*S_Y,+1/2+1*M_X,-1/3+1*S_X,-1/3+1*R_Y,+1/6+1*R_X,-5/6+1*Q_X,+2+1*F_Y,+1/2+1*U_Y,-1+1*L_X,-1/3+1*Q_Y,-1/3+1*K_Y,-1/2+1*N_X,-1+1*M_Y,-1/3+1*O_X,-1/3+1*K_X,-1/2+1*E_Y,-1+1*P_X,-3/2+1*T_X,-1/2+1*C_X,-1+1*N_Y,+1/2+1*A_Y,-1/2+1*B_X,-1/2+1*C_Y,+1/2+1*T_Y,+1/2+1*L_Y],[O_Y,U_X,P_Y,S_Y,M_X,S_X,R_Y,R_X,Q_X,F_Y,U_Y,L_X,Q_Y,K_Y,N_X,M_Y,O_X,K_X,E_Y,P_X,T_X,C_X,N_Y,A_Y,B_X,C_Y,T_Y,L_Y]);
print("A=(1,A_y,0) B_y=0 D=(1,0,0) E_x=0 F=(1,F_y,0) G=(0,1,0) H_x=0 H_y=1 I_x=1 I_y=0 J_x=0 J_y=0 ");

mathe

试验了一下，21棵树24行的第一个解中，把半自由的U点删除后，就是我们以前找到的20棵树23行中的第二组解（整数解）