数学研发网设为首页收藏本站
切换到窄版

 找回密码
 欢迎注册
数学研发论坛»论坛 › 【数学研究】 › 数学欣赏 › 果树种植最优解精美图形作法探讨
1 ...91011121314151617... 18下一页
返回列表 发新帖
楼主: wayne

[讨论] 果树种植最优解精美图形作法探讨

 火 [复制链接]
mathe
发表于 2019-12-19 20:40:13 来自手机 | 显示全部楼层
1. 变换矩阵最后一列不需要变为1。
2. 是矩阵的右边乘上列向量而不是行向量乘上矩阵
我计算的S就是变换阵,U1,V1,Q1,N1就是四点变换后的坐标，构成正方形.
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

数学星空
发表于 2019-12-19 22:04:22 | 显示全部楼层
经过楼上mathe的指点终于得到了想要的图形：

51.gif

123.gif

[-1.00000000031813, 0.384042943445230, A],
[3.49395921262253, 3.49395920827140, B],
[-3.49395920936664, 3.49395920766090, C],
[-3.49395921045821, -3.49395920661485, D],
[-9.09783468542929, 0.999999999819806, E],
[9.09783468859013, -0.999999999611732, F],
[-9.09783468537715, -0.999999999820944, G],
[1.00000000151713, 0.384042943514974, H],
[-1.00000000050038, -0.384042943042200, I],
[1.00000000128494, -0.384042942998411, J],
[3.49395920994264, -3.49395920682872, K],
[9.09783468972171, 1.00000000064339, L],
[-3.49395920997241, -0.384042943096800, M],
[1.00000000170342, 1.00000000027686, N],
[9.09783469113276, 3.49395920876099, O],
[9.09783468717907, -3.49395920700022, P],
[-1.00000000017199, 1.00000000018635, Q],
[3.49395921142987, 0.384042943601908, R],
[3.49395921113528, -0.384042942943769, S],
[-9.09783468531214, -3.49395920644334, T],
[1.00000000109864, -0.999999999704833, U],
[-1.00000000064661, -0.999999999727832, V],
[-9.09783468549431, 3.49395920717132, W],
[-3.49395920985244, 0.384042943358285, X]
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

数学星空
发表于 2019-12-20 19:28:45 | 显示全部楼层
很奇怪，用同样方法计算111#，也没得到mathe的图样，不知mathe能否指点一下？

由t^2-t-1=0,得到t=1.618033988和t=-0.6180339880

下面选择t=-0.6180339880计算得到；

[[A, 0., 1., 1.], [B, -0.3819660120, 0.500000000000000, 1.], [C, -0.2360679760, 0.072949018000000, 1.], [D, -2.2360679760, -0.309016994000000, 1.], [E, 0.3819660120, 0.309016994000000, 1.], [F, 1., 0., 1.], [G, 1., 1.30901699400000, 1.], [H, 0.2360679760, 0.309016994000000, 1.], [I, -0.6180339880, 0.500000000000000, 1.], [J, 0., 0.190983006000000, 1.], [K, 1., 0.309016994000000, 0.], [L, 1., -0.309016994000000, 0.], [M, -1., -0.309016994000000, 1.], [N, -0.2360679760, 0.690983006000000, 1.], [O, -0.6180339880, 0.809016994000000, 1.], [P, -0.6180339880, 0., 1.], [Q, 0.3819660120, 0.190983006000000, 1.], [R, 0.6180339880, 0.190983006000000, 1.], [S, -0.2360679760, 0.309016994000000, 1.], [T, 0., 0., 1.], [U, 0., 1., 0.], [V, 1., 0., 0.], [W, 1., -0.309016994000000, 1.], [X, 0.3819660120, 0.500000000000000, 1.]]

除掉无穷远点K, L, U, V ,画图得到：

125.gif

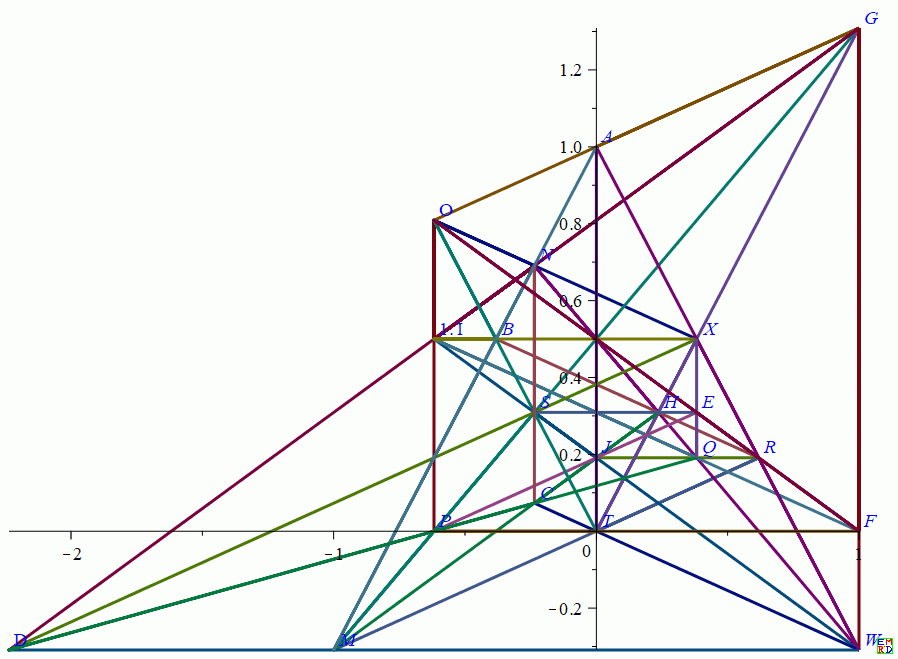
按照楼上的计算方法，选择四个点W,U,T,X做射影变换(取变换后WUT构成三角形的顶点，边长为1，X为正三角形的中心）

即W[1., -0.309016994000000, 1.]->[0,sqrt(3)/3,1],  U[ 0., 1., 0.]->[-1/2,-sqrt(3)/6,1] ,   T[0., 0., 1.]->[1/2,-sqrt(3)/6,1] ,    X[0.3819660120, 0.500000000000000, 1.]->[0,0,1]

求得射影变换矩阵J1为： [[-0.6545084975, -0.5000000000, 0.5000000005], [1.133641970, -0.2886751347, -0.2886751351], [0.9270509787, 1.000000000, 1.000000001]])

注：楼下mathe得到的变换矩阵J2为 [[0.3530056650, 0.2696723314, -0.2696723318], [-0.6114237460, 0.1556953931, 0.1556953933], [-0.4999999974, -0.5393446628, -0.5393446636]]；

  J1,J2若将每行都化为z=1,就是一样均为 [[-1.309016994, -0.9999999988, 1], [-3.927050974, 0.9999999986, 1], [0.9270509774, 0.9999999986, 1]]

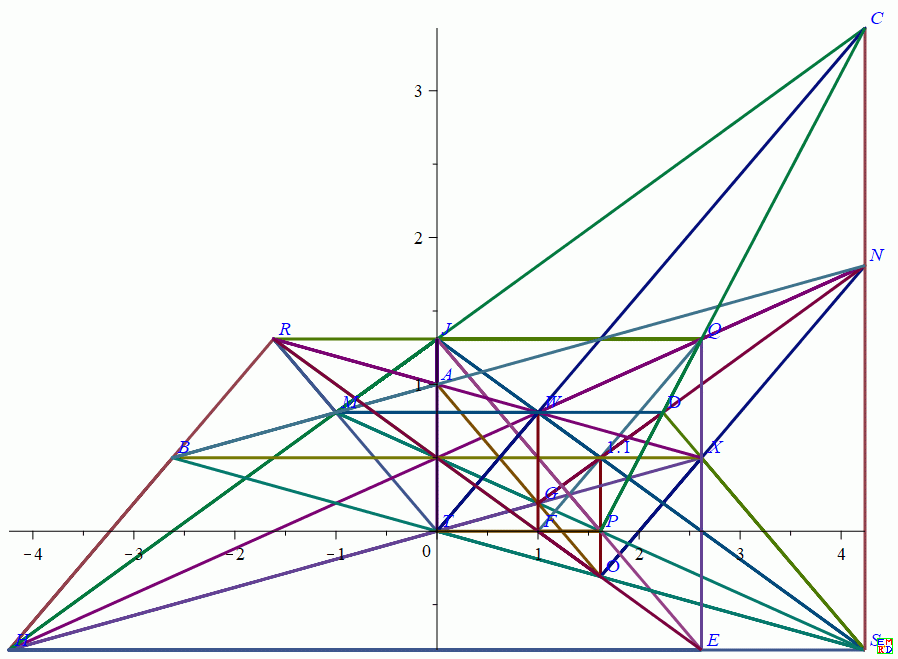
由J1射影变换得到

[2.50000020560093*10^(-10), -0.288675134755662, A], [0.436338998334175, -0.755761313617648, B], [0.723606792750855, -0.675973464288759, C], [-1.53262380618613, 1.97860882314602, D], [0.0574171211872823, 0.0331497903437648, E], [-0.0801787283406760, 0.438476638034528, F], [-0.250000000177685, 0.144337566957350, G], [0.125000001192225, -0.0721687853002482, H], [0.706011326427899, -1.22284748665600, I], [0.339642543279377, -0.288675134793473, J], [-0.654508499830173, 0.844966838960361, K], [-0.809017000485346, 1.97860881867382, L], [-5.54508511075584, 5.64715142478797, M], [0.209910634904626, -0.513377387649850, N], [0.404508496175841, -0.989304399716518, O], [2.11803396725287, -2.31659551579066, P], [0.0999999997827559, 0.0577350267694893, Q], [3.45924335493919*10^(-10), 0.202287890613122, R], [0.458644086862735, -0.592106968939316, S], [0.500000000000000, -0.288675134811325, T], [-0.500000000000000, -0.288675134700000, U], [-0.706011333290230, 1.22284749819228, V], [6.86155565604419*10^(-17), 0.577350269230219, W], [-5.94287545476067*10^(-11), -7.18818497189416*10^(-11), X]

画图显示比较杂乱，肯定是哪里出了问题？？点 [-5.54508512863216, 5.64715144008720, M]比较异类离的较远，难道是因为选择作变换的四个点（WUTX)中有一个无穷远点U造成的？？？
124.gif
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-20 19:49:22 来自手机 | 显示全部楼层
你怎么计算的？显然你计算出来W,U,X,T的坐标都不符合要求

点评

mathe
不能这样算  发表于 2019-12-20 21:23
数学星空
我的计算方法：设3*3阶变换矩阵为S,四个点变换前的矩阵（4*3）为T，四个点变换后的矩阵为（4*3)为M,则有先计算N=(S*T~)~，然后将N的最后一列化为1记为N1,使N1=M,求S,其中~表转置矩阵  发表于 2019-12-20 21:21
mathe
我是直接用你的数值结果  发表于 2019-12-20 21:17
数学星空
由于我选的t=1.618033988 , 你选的另一个根t=-0.6180339880； 所以我们的WUTX坐标不一样，为了方便讨论，我将楼上更新为t=-0.6180339880，这样就一样了  发表于 2019-12-20 20:51
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-20 19:55:38 | 显示全部楼层
直接对上次代码改数据(字母名称就不改了，所以和你的不匹配）
Q=[1., -0.309016994000000, 1.];
V=[0., 1., 0.];
U=[0., 0., 1.];
N=[0.3819660120, 0.500000000000000, 1.];
T=matrix(12,13);
for(u=1,3, T[1,u]=Q[u]); T[1,10]=0;
for(u=1,3,T[2,u+3]=Q[u]); T[2,10]=sqrt(3)/3;
for(u=1,3,T[3,u+6]=Q[u]); T[3,10]=1;
for(u=1,3, T[4,u]=V[u]); T[4,11]=-1/2;
for(u=1,3,T[5,u+3]=V[u]); T[5,11]=-sqrt(3)/6;
for(u=1,3,T[6,u+6]=V[u]); T[6,11]=1;
for(u=1,3, T[7,u]=U[u]); T[7,12]=1/2;
for(u=1,3,T[8,u+3]=U[u]); T[8,12]=-sqrt(3)/6;
for(u=1,3,T[9,u+6]=U[u]); T[9,12]=1;
for(u=1,3, T[10,u]=N[u]); T[10,13]=0;
for(u=1,3,T[11,u+3]=N[u]); T[11,13]=0;
for(u=1,3,T[12,u+6]=N[u]); T[12,13]=1;
R=matker(T)~[1,1..9];
S=matrix(3,3);
for(u=1,3,S[1,u]=R[u];S[2,u]=R[u+3];S[3,u]=R[u+6])
Q1=S*Q~;Q1=Q1/Q1[3]
V1=S*V~;V1=V1/V1[3]
U1=S*U~;U1=U1/U1[3]
N1=S*N~;N1=N1/N1[3]
S

结果:
(19:54) gp > Q1=S*Q~;Q1=Q1/Q1[3]
%21 = [-1.6837458349204428006 E-39, 0.57735026918962576450914878050195745565, 1.0000000000000000000000000000000000000]~
(19:54) gp > V1=S*V~;V1=V1/V1[3]
%22 = [-0.50000000000000000000000000000000000000, -0.28867513459481288225457439025097872783, 1.0000000000000000000000000000000000000]~
(19:54) gp > U1=S*U~;U1=U1/U1[3]
%23 = [0.50000000000000000000000000000000000000, -0.28867513459481288225457439025097872783, 1.0000000000000000000000000000000000000]~
(19:54) gp > N1=S*N~;N1=N1/N1[3]
%24 = [0.E-38, -1.4693679385278593850 E-39, 1.0000000000000000000000000000000000000]~
(19:54) gp > S
%25 =
[0.35300566500580979821686888073655703564 0.26967233141969409948074188814222945992 -0.26967233178552417519579306157296104348]

[-0.61142374604378055516562730110475899584 0.15569539313815436224534312637626872883 0.15569539334936645493708909649317362345]

[-0.49999999740620259722917961798090153930 -0.53934466283938819896148377628445891984 -0.53934466357104835039158612314592208695]

点评

数学星空
12*13的矩阵没有正交基吧？好像只有正方(n*n)矩阵才能求正交基吧？  发表于 2019-12-21 13:40
mathe
matker(T)表示找出和矩阵所有行都正交的向量构成空间的一组基。而这里结果实际上是一个13*1的矩阵。~表示转置，成1*13矩阵。然后[1,1..9]表示取其第一行前9个元素。  发表于 2019-12-21 09:05
数学星空
T[1,i]=0, i=4...9 默认为0? R=matker(T)~[1,1..9]表示列矩阵1*9的T,matker是什么? Q~表Q的转置矩阵?  发表于 2019-12-20 22:38
数学星空
T=matrix(12,13) 表示12*13阶矩阵? for(u=1,3, T[1,u]=Q[u])表示T[1,1]=Q[1],T[1,2]=Q[2],T[1,3]=Q[3]?  发表于 2019-12-20 22:32
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-20 20:53:24 | 显示全部楼层
113#的一些解也可以试验一下，比如:
ADGJBEIJCDHKAFIKCEGLBFHLCJMODINODLMPAHNPGKOPBGMQFJNQAEOQEHMRBKNRCFPRILQRABCSDEFSGHITJKLTMNST
Start group:
ABCDEFGHIJKLMNOPQRST 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22
GHIJKLABCDEFNMOQPRTS 00 02 01 04 03 05 07 06 12 11 13 09 08 10 15 14 17 16 20 21 18 19 22
EDFBACIHGJLKNMQROPST 01 00 05 04 03 02 12 11 15 14 17 07 06 13 09 08 16 10 19 18 20 21 22
CBADFEKJLHGINMPORQST 02 05 00 04 03 01 09 08 07 06 10 15 14 16 12 11 13 17 18 19 21 20 22
IHGJLKEDFBACMNQORPTS 01 05 00 03 04 02 11 12 06 07 13 14 15 17 08 09 10 16 20 21 19 18 22
KJLHGICBADFEMNPROQTS 02 00 05 03 04 01 08 09 14 15 16 06 07 10 11 12 17 13 21 20 18 19 22
FDEBCALJKHIGMNRQPOST 05 02 01 03 04 00 14 15 11 12 17 08 09 16 06 07 13 10 19 18 21 20 22
LJKHIGFDEBCANMRPQOTS 05 01 02 04 03 00 15 14 09 08 16 12 11 17 07 06 10 13 21 20 19 18 22
这是一个8阶置换，里面好像包含四阶置换（AIFK)，所以可以试验把这四个点依次映射成一个正方形顶点看看。

        Parameter [-1+4*t+1*t^2=0]
        A[+1 ,0 , 0]
        B[0 ,+1 , +1]
        C[-1 ,+1 , +1]
        D[+1 ,-1/2-1/2*t , 0]
        E[0 ,+1/2+1/2*t , +1]
        F[+1 ,0 , +1]
        G[+1 ,-1/2+1/2*t , 0]
        H[+3/2+1/2*t ,-1/2-1/2*t , +1]
        I[0 ,0 , +1]
        J[0 ,+1 , 0]
        K[+1/2+1/2*t ,0 , +1]
        L[+1/2+1/2*t ,+1/2-1/2*t , +1]
        M[-1 ,+3/2-1/2*t , +1]
        N[+1 ,-1/2-1/2*t , +1]
        O[-1 ,+1/2+1/2*t , +1]
        P[+2+1*t ,-1/2-1/2*t , +1]
        Q[+1 ,+1/2+1/2*t , +1]
        R[+2/5+1/5*t ,+3/10-1/10*t , +1]
        S[-1/2-1/2*t ,+1 , +1]
        T[+1/2+1/2*t ,-1*t , +1]

点评

数学星空
你可以把每个点的坐标方程提供一下，我们可以试一下哈？  发表于 2019-12-24 20:16
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-20 20:58:14 | 显示全部楼层
CFGNCHIODGKQEFJPDIJREHKSJKNOGIPSFHQRFIKLGHJMDLNPEMNQCLQSCMPRDMOSELORBNRSAOPQABLM
Start group:
ABCDEFGHIJKLMNOPQRS 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19
BAECDJFKHIGMLPSRNOQ 03 05 00 04 01 02 07 08 06 10 09 14 11 12 16 13 15 18 17 19
BACDEHIFGKJMLONSRQP 01 00 04 05 02 03 06 07 08 10 09 15 16 14 13 11 12 18 17 19
ABDECIJGKHFLMRQOPSN 04 02 03 01 05 00 08 06 07 09 10 16 14 11 15 12 13 17 18 19
ABECDKHJFGILMSPQONR 05 03 01 02 00 04 07 08 06 09 10 13 15 16 12 14 11 17 18 19
BADCEKGJIHFLMQRSNOP 02 04 00 05 01 03 08 07 06 09 10 13 12 11 15 14 16 18 17 19
ABCEDGFIHKJMLNOQPSR 00 01 03 02 05 04 06 08 07 10 09 12 11 14 13 16 15 17 18 19
BAEDCFJHKGILMPSNRQO 03 05 04 00 02 01 07 06 08 09 10 11 14 16 12 15 13 18 17 19
BACEDIHGFJKLMONRSPQ 01 00 05 04 03 02 06 08 07 09 10 16 15 13 14 12 11 18 17 19
ABDCEJIKGFHMLRQPONS 04 02 01 03 00 05 08 07 06 10 09 14 16 15 11 13 12 17 18 19
ABEDCHKFJIGMLSPOQRN 05 03 02 01 04 00 07 06 08 10 09 15 13 12 16 11 14 17 18 19
BADECGKIJFHMLQRNSPO 02 04 05 00 03 01 08 06 07 10 09 12 13 15 11 16 14 18 17 19
可以试验CDE映射为正三角形，M为中心

这个只有复数解:
        [+1*t^2+1/3]
        -1*v11-1*t
        +1*v1-3/2*v11-1/2
        +1*v0+3/2*v11-1/2
        +1*v2-3/2*v11-1/2
        +1*v3-3/2*v11-1/2
        +1*v4-1/2*v11-1/2
        +1*v5-1/2*v11-1/2
        +1*v6+3/2*v11-1/2
        +1*v7+3/2*v11-1/2
        +1*v8-1*v11-1
        +1*v9-1*v11
        +1*v10-1*v11-1
        A(v6,v2)
        B(v3,v7)
        C(v5,v4)
        D(+0,+0)
        E(+1,+1)
        F(v5,v8)
        G(v5,v9)
        H(v10,v4)
        I(v11,v4)
        J[+1,v0,0];
        K[+1,v1,0];
        L(+0,+1)
        M(+1,+0)
        N[+0,+1,0];
        O[+1,+0,0];
        P(+0,v2)
        Q(+1,v2)
        R(v3,+1)
        S(v3,+0)

点评

mathe
是的，复数解就不能作图了  发表于 2019-12-28 16:48
数学星空
这个复数解没办法画图哈~~  发表于 2019-12-25 19:55
数学星空
你可以把每个点的坐标方程提供一下，我们可以试一下哈？  发表于 2019-12-24 20:16
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

数学星空
发表于 2019-12-23 18:50:19 | 显示全部楼层
125# mathe的计算方法，我不太确定下面理解是否正确：

设变换前的四点坐标 \(Q=[Q_1,Q_2,Q_3],V=[V_1,V_2,V_3],U=[U_1,U_2,U_3],N=[N_1,N_2,N_3]\)

变换后的四点坐标\(Q1=[Q1_1,Q1_2,Q1_3],V1=[V1_1,V1_2,V1_3],U1=[U1_1,U1_2,U1_3],N1=[N1_1,N1_2,N1_3]\)

构造12X13阶矩阵：

\[T = \begin{pmatrix}
Q_{1}&Q_{2}& Q_{3}&0&0&0&0&0&0&Q1_{1}&0&0&0\\
0&0&0&Q_{1}&Q_{2}&Q_{3}&0&0&0&Q1_{2}&0&0&0\\
0&0&0&0&0&0&Q_{1}&Q_{2}&Q_{3}&Q1_{3}&0&0&0\\
V_{1}&V_{2}&V_{3}&0&0&0&0&0&0&0&V1_{1}&0&0\\
0&0&0&V_{1}&V_{2}&V_{3}&0&0&0&0&V1_{2}&0&0\\
0&0&0&0&0&0&V_{1}&V_{2}&V_{3}&0&V1_{3}&0&0\\
U_{1}&U_{2}&U_{3}&0&0&0&0&0&0&0&0&U1_{1}&0\\
0&0&0&U_{1}&U_{2}&U_{3}&0&0&0&0&0&U1_{2}&0\\
0&0&0&0&0&0&U_{1}&U_{2}&U_{3}&0&0&U1_{3}&0\\
N_{1}&N_{2}&N_{3}&0&0&0&0&0&0&0&0&0&N1_{1}\\
0&0&0&N_{1}&N_{2}&N_{3}&0&0&0&0&0&0&N1_{2}\\
0&0&0&0&0&0&N_{1}&N_{2}&N_{3}&0&0&0&N1_{3}
\end{pmatrix}_{12 \times 13 } \]

然后求解$TR=0$的非零解\(R=[R_1,R_2,R_3,R_4,R_5,R_6,R_7,R_8,R_9,R_{10},R_{11},R_{12}, R_{13}]\)  

(maple的求解命令为NullSpace）

则可以得到变换矩阵S为

\[S = \begin{pmatrix}
R_1&R_2&R_3\\
R_4&R_5&R_6\\
R_7&R_8&R_9
\end{pmatrix}_{3 \times 3 }\]

注：楼上123#的结果比较

利用我得到的变换矩阵J1可以得到

317.gif

利用mathe的变换矩阵J2可以得到




好像结果几乎是一样的，问题是都不是我们想要的答案！！！我也没有找到到底哪里出了问题？



318.gif

点评

mathe
那就是点选择的不对，需要变换其它的点为正三角形  发表于 2019-12-24 18:52
数学星空
根据变换后的图形可以看出WUTX的确已变成了正三角形的顶点及中心，但是其余点都是在这个小三角形的外围，若能将其余点变到这个正三角形内部应该就是我们想要的图形  发表于 2019-12-23 22:00
mathe
另外变换阵需要对列向量而不是行向量做变换  发表于 2019-12-23 20:39
mathe
R是使得TR=0的非零解。  发表于 2019-12-23 18:53
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-24 08:08:08 | 显示全部楼层
分析思路如下，
设变换矩阵\(S=\begin{pmatrix}R_1&R_2&R_3\\R_4&R_5&R_6\\R_7&R_8&R_9\end{pmatrix}\)将
\(Q=\begin{pmatrix}Q_1\\Q_2\\Q_3\end{pmatrix},V=\begin{pmatrix}V_1\\V_2\\V_3\end{pmatrix},U=\begin{pmatrix}U_1\\U_2\\U_3\end{pmatrix},N=\begin{pmatrix}N_1\\N_2\\N_3\end{pmatrix}\)变换为\(Q1=\begin{pmatrix}Q1_1\\Q1_2\\Q1_3\end{pmatrix},V1=\begin{pmatrix}V1_1\\V1_2\\V1_3\end{pmatrix},U1=\begin{pmatrix}U1_1\\U1_2\\U1_3\end{pmatrix},N1=\begin{pmatrix}N1_1\\N1_2\\N1_3\end{pmatrix}\)
于是存在常数\(-R_{10},-R_{11},-R_{12},-R_{13}\)使得
\(SQ=-R_{10} Q1,SV=-R_{11} V1， SU=-R_{12} U1, SN=-R_{13} N1\)
展开后就出现楼上的矩阵$T$了,即
\(T\begin{pmatrix}R_1\\R_2\\R_3\\R_4\\R_5\\R_6\\R_7\\R_8\\R_9\\R_{10}\\R_{11}\\R_{12}\\R_{13}\end{pmatrix}=0\).
解这个方程得出任意的非零向量，取前9个分量构成矩阵S即可

点评

数学星空
嗯，搞明白了，多谢指点哈  发表于 2019-12-24 19:18
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

mathe
发表于 2019-12-24 15:13:35 | 显示全部楼层
75#的20棵树23行可以做出一种更加对称的形式，只是直线CDJK是无穷远直线:
s20f.png
毋因群疑而阻独见　　毋任己意而废人言
毋私小惠而伤大体　　毋借公论以快私情
回复 支持 反对

使用道具 举报

1 ...91011121314151617... 18下一页
返回列表 发新帖
高级模式
B Color Image Link Quote Code Smilies
您需要登录后才可以回帖 登录 | 欢迎注册

本版积分规则

小黑屋|手机版|数学研发网 ( 苏ICP备07505100号 )

GMT+8, 2025-3-9 10:34 , Processed in 0.038563 second(s), 18 queries .

Powered by Discuz! X3.5

© 2001-2025 Discuz! Team.

快速回复 返回顶部 返回列表