三角形的心迹

hujunhua

三角形的心迹

        近日困在陕蒙边界附近的一个沙漠乡镇，百无聊奈，思考一个几何问题，感觉有点趣味，惜未带本本，没有几何画板辅助，不得窥其心迹。
       先发出来给@数学星空 等解难高手们研究，我就捡现成的欣赏吧。故发在数学欣赏版块。

        定义1（三角形的线性中心）△ABC 内一点 P 向三边所张的角∠BPC, ∠CPA, ∠APB分别记为 P(A), P(B), P(C)，若对X=A, B, C都成立P(X)=m∠X+nπ/3  (m, n为常系数), 就称P为△ABC 的一个线性中心, 并记为LH(m, n)。
        *注1: 由ΣP(X)=2π 知 m+n=2, 所以P(X)=m(∠X-π/3)+2π/3. 记δ(X)=∠X-π/3, 称为三角形内角的角偏（与平均值的偏差），再记Δ(X)=P(X)-2π/3，称为周角P的各分角的角偏，定义1中的张角式可化为Δ(X)=m·δ(X).  即线性中心乃是分角角偏与内角角偏对应成比例的点。
        *注2: 定义可延伸到三角形边上以及外部，取张角时保持三者在P点合围一个周角, 并保持各分角的连续性.（特别是在三角形边上).

        线性中心之名的合理性在于: P(X)是线性函数，并对三个顶点平等成立，LH(m, n)又唯一，堪称中心。

        易验证，LH(2, 0)为外心，LH(1/2, 3/2)为内心，LH(-1, 3)为垂心，LH(0, 2)为等角中心

        定义2（三角形的心迹）当(m, n)在直线m+n=2上滑动时，LH(m, n)就在△ABC 所在平面上滑动，其轨迹称为△ABC 的心迹。

hujunhua

        由于外心、内心、垂心一般不共线，可知三角形的心迹一般不是直线（欧拉线），这就有点不单调了。它会是一个什么曲线呢？让我先猜测一下。
        正三角形的心迹退化为一点，等腰三角形的心迹退化为一条直线，3点决定一个心迹. …，慢着，等一等，这好像是圆的特征哦。

        真的是一个圆吗，那圆心应该是一个很特别的心了，是什么呢？肯定不是重心，因为重心是外心和垂心连线的三等分点，而非中点，等腰三角形的重心也不是无穷远点。
        难道三角形的外心、内心、垂心和等角中心是共圆的？

ps: 重心一般不是一个线性中心，因为重心具有仿射不变性，而线性中心没有。对于心迹而言，重心恐怕啥都不是，即两者木啥关系。

hujunhua

        由定义1的注2，当有0<P(X)<2π，即0<m(∠X-π/3)+2π/3<2π. 假定∠A≤∠B≤∠C, 那么∠A≤π/3≤∠C，由此可得

-2π/(3∠C-π)<m<2π/(π-3∠A)

有限的定义域会导致心迹的残缺吗？

hujunhua

LH(1, 1)是一个有趣的点吗？

数学星空

当\(m=1\)时，记\(\triangle ABC\)的三边分别为\(a,b,c\),LH(1,1)记为\(X\),\(\angle AXB=\gamma,\angle{AXC}=\beta,\angle{BXC}=\alpha\)

根据定义有：

\(\alpha=\angle A+\frac{\pi}{3}\).....................(1)

\(\beta=\angle B+\frac{\pi}{3}\)......................(2)

\(\gamma=\angle C+\frac{\pi}{3}\)..................(3)

\(\alpha+\beta+\gamma=2\pi\)........................(4)

转化为代数方程如下：

\(a^2=y^2+z^2-2yz\cos(\angle A+\frac{\pi}{3})\)...........................(5)

\(b^2=x^2+z^2-2xz\cos(\angle B+\frac{\pi}{3})\)...........................(6)

\(c^2=x^2+y^2-2yx\cos(\angle C+\frac{\pi}{3})\)...........................(7)

\((-a^2+y^2+z^2)^2x^2+(-b^2+x^2+z^2)^2y^2+(-c^2+x^2+y^2)^2z^2-(-a^2+y^2+z^2)(-b^2+x^2+z^2)(-c^2+x^2+y^2)-4z^2y^2x^2=0\).............(8)

进一步将三角形余弦公式代入得到：

\(a^4b^2c^2-a^4bcyz+a^4y^2z^2+a^2b^3cyz-2a^2b^2c^2y^2-2a^2b^2c^2z^2-2a^2b^2y^2z^2+a^2bc^3yz+a^2bcy^3z+a^2bcyz^3-2a^2c^2y^2z^2+b^4y^2z^2-b^3cy^3z-b^3cyz^3+b^2c^2y^4+b^2c^2y^2z^2+b^2c^2z^4-bc^3y^3z-bc^3yz^3+c^4y^2z^2=0\)

\(a^4x^2z^2+a^3b^2cxz-a^3cx^3z-a^3cxz^3+a^2b^4c^2-2a^2b^2c^2x^2-2a^2b^2c^2z^2-2a^2b^2x^2z^2+a^2c^2x^4+a^2c^2x^2z^2+a^2c^2z^4-ab^4cxz+ab^2c^3xz+ab^2cx^3z+ab^2cxz^3-ac^3x^3z-ac^3xz^3+b^4x^2z^2-2b^2c^2x^2z^2+c^4x^2z^2=0\)

\(a^4x^2y^2+a^3bc^2xy-a^3bx^3y-a^3bxy^3+a^2b^2c^4-2a^2b^2c^2x^2-2a^2b^2c^2y^2+a^2b^2x^4+a^2b^2x^2y^2+a^2b^2y^4-2a^2c^2x^2y^2+ab^3c^2xy-ab^3x^3y-ab^3xy^3-abc^4xy+abc^2x^3y+abc^2xy^3+b^4x^2y^2-2b^2c^2x^2y^2+c^4x^2y^2=0\)

最终求解得到：

\(b^4c^4-b^2c^2(a^2+b^2+c^2)x^2+(a^4-a^2b^2-a^2c^2+b^4-b^2c^2+c^4)x^4=0\)

\(a^4c^4-a^2c^2(a^2+b^2+c^2)y^2+(a^4-a^2b^2-a^2c^2+b^4-b^2c^2+c^4)y^4=0\)

\(a^4b^4-a^2b^2(a^2+b^2+c^2)z^2+(a^4-a^2b^2-a^2c^2+b^4-b^2c^2+c^4)z^4=0\)

例：取\(a=3,b=4,c=4.5\) 求解得：

\({x = 2.745023224,y = 2.058767418,z = 1.830015482}\)

\({x = 11.99591196,y = 8.996933967,z = 7.997274638}\)

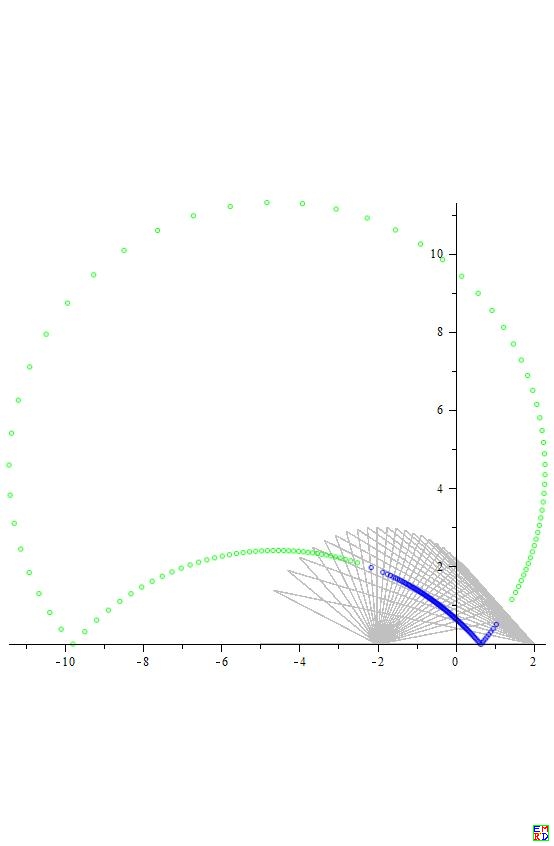
我们对\({a=3,b=4,c=1+\frac{6k}{100},k=1..100}，A[2,0],C[-2,0],|BC|=3\)，共100个三角形（灰色三角形），计算其\(m=1\)时的心构成两条曲线具体见下图蓝色（三角形内），绿色（三角形外）：

hujunhua

@数学星空 如果有几何画图工具，也可以不用解方程, 可以直接几何绘图. 边长3为弦, 弧含角A+π/3作一段弧, 再以边长4为弦, 弧含角B+π/3作一段弧, 两弧在三角形内的交点就是。显然，只要三角形的最大内角小于2π/3，LH(1,1)必在形内。

hujunhua

在店家电脑上现装现画了一下

a=3,b=4,c=4.5
x=2.74502, y=2.05877, z=1.83002
图传不上来，一直在转圈圈。一会用手机传传看。

手机也传不了，传到本坛qq群吧。

/

终于搞掂了.

mathe

感觉自相交点都在三角形顶点，对于哪些m会落在顶点上呢?

wayne

既然$m+n=2$恒成立，索性就 简化成 单变量 $L(m) = LH(m,2-m)$

当仅有一个角为60°时，比如 ∠B = 60°时，心迹图会退化成 一个圆。

wayne

心迹的曲线方程可以写成参数形式｛x=x(m), y=y(m).  曲线形状取决于三角形的形状,  很可能跟三个内角角偏的比例有关。

https://www.geogebra.org/m/xdrbcJne

我把geogebra文件上传了。安装软件即可动态展示， 也可以在网页端耍耍。