求三角形内的相交三角形面积

数学星空

如下图所示，设

\(\frac{AK}{AB}=k_1,\frac{BI}{BC}=k_2,\frac{CJ}{CA}=k_3\),

\(\angle DKB=\alpha,\angle CIE=\beta,\angle AJF=\gamma\)

\(\triangle ABC\)的三边长分别为\(a,b,c\),面积为\(S\)

请求出\(\triangle DEF\)的面积\(s\)?

manthanein

我觉得可以先用三角函数算出三条边的长，然后通过三条边的长算出三角形的面积。
不过可能有点繁。

wayne

这个解应该很复杂吧,因为 D,E,F 三个点都在三角形ABC内部的 判断分支比较多.

数学星空

当\(\alpha=\beta=\gamma\)时，叶中豪老师给出了表达式：

数学星空

我们可以建立坐标系求解：

\(A[0, h],B[-u, 0],C[v, 0],I[vk_2-(1-k_2)u, 0],J[(1-k_3)v, hk_3],K[-uk_1, (1-k_1)h],D[x_1, y_1],E[x_2, y_2],F[x_3, y_3]\)

\(h=\frac{\sqrt{-a^4+2a^2b^2+2a^2c^2-b^4+2b^2c^2-c^4}}{2a},u=\frac{a^2-b^2+c^2}{2a},v=\frac{a^2+b^2-c^2}{2a}\)

\(s=\frac{x_1y_2-x_1y_3-x_2y_1+x_2y_3+x_3y_1-x_3y_2}{2}\)

\(m=\tan(\alpha),n=\tan(\beta),p=\tan(\gamma)\)

\(x_1=-\frac{-hk_2mnu-hk_2mnv+h^2k_1m+hmnu+k_1mu^2+k_2nu^2+k_2nuv-h^2m-nu^2+hu}{hmn+mu-nu+h},y_1=\frac{-n(h^2k_1m+k_1mu^2+k_2mu^2+k_2muv-h^2m+hk_2u+hk_2v-mu^2)}{hmn+mu-nu+h}\)

\(x_2=\frac{hk_2npu+hk_2npv+h^2k_3p-hnpu+k_2nuv+k_2nv^2+k_3pv^2-nuv-pv^2+hv}{hnp+nv-pv+h},y_2=\frac{n(h^2k_3p+k_2puv+k_2pv^2+k_3pv^2-hk_2u-hk_2v-puv-pv^2+hu+hv)}{hnp+nv-pv+h}\)

\(x_3=\frac{h^3k_1mp+h^3k_3mp+hk_1mpu^2+hk_3mpv^2-h^3mp+h^2k_1mv-h^2k_3pu-hmpv^2+k_1mu^2v-k_3puv^2+h^2pu+puv^2}{-hmpu-hmpv+h^2m-h^2p-muv+puv-hu-hv}\)

\(y_3 = -\frac{-h^2k_1mpv+h^2k_3mpu-k_1mpu^2v+k_3mpuv^2+h^3k_1m+h^3k_3p+h^2mpv+hk_1mu^2+hk_3pv^2-mpuv^2-h^3m+hmuv-hpuv-hpv^2+h^2u+h^2v}{-hmpu-hmpv+h^2m-h^2p-muv+puv-hu-hv}\)

由于最终的表达式太长，不方便粘贴

例如：取\(u =1, v=2, h=\sqrt{3},m=n=p=\sqrt{3},\alpha=\beta=\gamma=\frac{\pi}{3},k_1=k_2=k_3=\frac{1}{3}\)

得到\(a=3,b=\sqrt{7},c=2,x_1=\frac{1}{6},y_1=\frac{\sqrt{3}}{6},x_2=\frac{1}{12},y_2=\frac{\sqrt{3}}{12},x_3=\frac{2}{9},y_3=\frac{\sqrt{3}}{9}\)



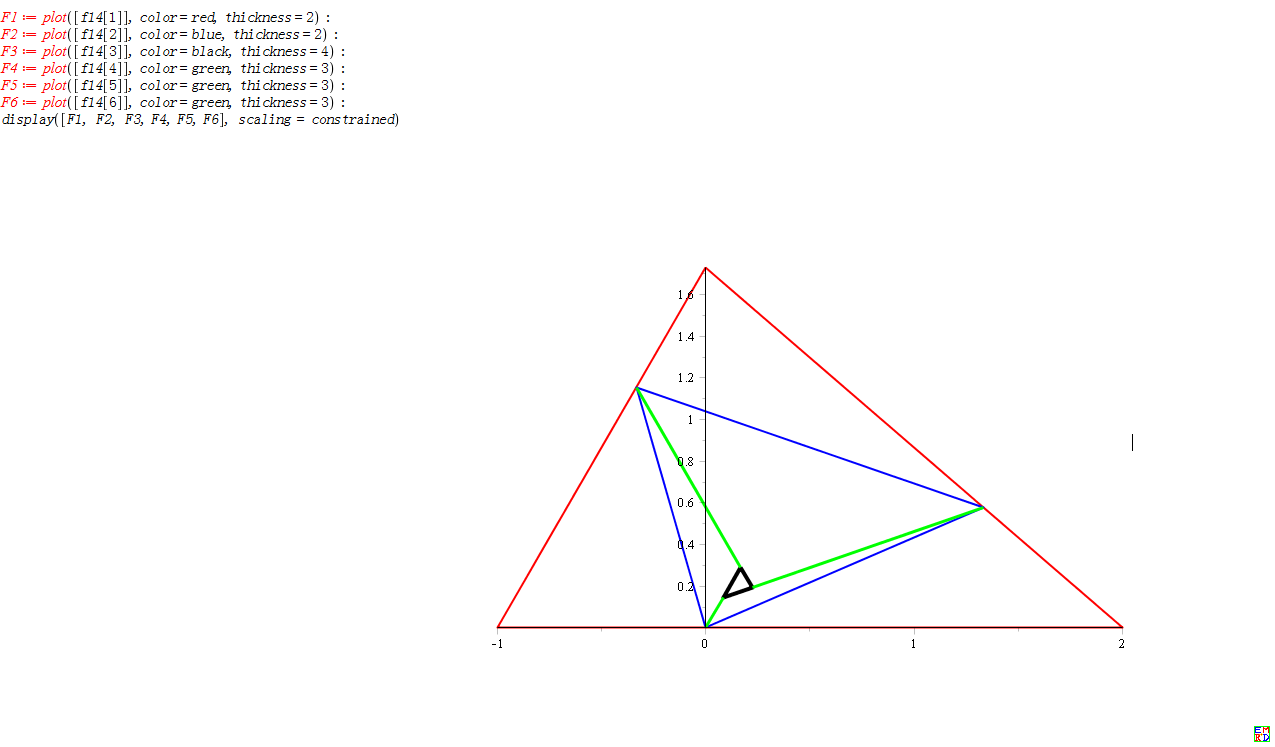
当然取\(\alpha=\beta=\gamma=\theta\)，即\(t=\tan(\alpha)=\tan(\beta)=\tan(\gamma)\) 结果化简后与叶中豪给出的一致

\((4a^4k_2^2t^2+8a^2b^2k_2k_3t^2+8a^2c^2k_1k_2t^2+4b^4k_3^2t^2+8b^2c^2k_1k_3t^2+4c^4k_1^2t^2-4a^4k_2t^2-4a^2b^2k_2t^2-4a^2b^2k_3t^2-4a^2c^2k_1t^2-4a^2c^2k_2t^2-4b^4k_3t^2-4b^2c^2k_1t^2-4b^2c^2k_3t^2-4c^4k_1t^2+a^4t^2+2a^2b^2t^2+2a^2c^2t^2+b^4t^2+2b^2c^2t^2+c^4t^2+a^4-2a^2b^2-2a^2c^2+b^4-2b^2c^2+c^4)^2-16t(t^2+1)(-c+a+b)(c+a+b)(-b+c+a)(a-b-c)(2a^2k_2+2b^2k_3+2c^2k_1-a^2-b^2-c^2)s+16(t^2+1)^2(-c+a+b)(c+a+b)(-b+c+a)(a-b-c)s^2=0\)

进一步取\(k_1=k_2=k_3=k\)得：

\(((a^4+2a^2b^2+2a^2c^2+b^4+2b^2c^2+c^4)(2k-1)^2t^2+16S^2)^2+256t(t^2+1)S^2(2k-1)(a^2+b^2+c^2)s-256(t^2+1)^2S^2s^2＝0\)

creasson

记\[\angle CDZ = \theta ,\angle AEX = \varphi ,\angle BFT = \phi \]
并设\[Z{\rm{ = }}\alpha C + \beta D + \gamma E(\alpha  + \beta  + \gamma  = 1)\]
于是\[\left\{ \begin{array}{l}
{\left( {\frac{{{S_{CDZ}}}}{{{S_{CDE}}}}} \right)^2} = {\gamma ^2} = {\left( {\frac{{DZ \times \sin \theta }}{{EC \times \sin C}}} \right)^2} \\
{\left( {\frac{{{S_{CEZ}}}}{{{S_{CED}}}}} \right)^2} = {\beta ^2} = {\left( {\frac{{EZ \times \sin \varphi }}{{DC \times \sin C}}} \right)^2} \\
\end{array} \right.\]
代入：\[\left\{ \begin{array}{l}
D{Z^2} = \alpha C{D^2} + \gamma D{E^2} - \left( {\alpha \beta C{D^2} + \beta \gamma D{E^2} + \gamma \alpha E{C^2}} \right) \\
E{Z^2} = \alpha E{C^2} + \beta D{E^2} - \left( {\alpha \beta C{D^2} + \beta \gamma D{E^2} + \gamma \alpha E{C^2}} \right) \\
\end{array} \right.\]
得到方程组：\[\left\{ \begin{array}{l}
\alpha  + \beta  + \gamma  = 1 \\
{\gamma ^2}E{C^2} \times {\sin ^2}C = \left( {\alpha C{D^2} + \gamma D{E^2} - \alpha \beta C{D^2} - \beta \gamma D{E^2} - \gamma \alpha E{C^2}} \right){\sin ^2}\theta  \\
{\beta ^2}C{D^2} \times {\sin ^2}C = \left( {\alpha E{C^2} + \beta D{E^2} - \alpha \beta C{D^2} - \beta \gamma D{E^2} - \gamma \alpha E{C^2}} \right){\sin ^2}\varphi  \\
\end{array} \right.\]
这可化为单未知数的四次方程，我不喜欢做繁琐的计算，于是此处略掉过程。
于是自然可求出点$Z$关于 $A,B,C$的仿射坐标，记为
\[Z = {x_1}A + {y_1}B + {z_1}C\]
同理，求出\[X = {x_2}A + {y_2}B + {z_2}C\]
\[Y = {x_3}A + {y_3}B + {z_3}C\]
则三角形$\Delta XYZ$的面积
\[{S_{XYZ}} = {S_{ABC}} \times |\det \left( {\begin{array}{*{20}{c}}
   {{x_1}} & {{y_1}} & {{z_1}}  \\
   {{x_2}} & {{y_2}} & {{z_2}}  \\
   {{x_3}} & {{y_3}} & {{z_3}}  \\
\end{array}} \right)|\]

附一般距离公式：假设$Q,T$是$N$个点$P_1,P_2,P_3,...P_N$所确定的$N$维空间中的两点，并且
$Q$关于这$N$个点的仿射坐标是\[Q = {\alpha _1}{P_1} + {\alpha _2}{P_2} + {\alpha _3}{P_3} + ... + {\alpha _n}{P_n}\left( {\sum\limits_{i = 1}^n {{\alpha _i} = 1} } \right)\]
那么,$QT$距离的平方是:
\[Q{T^2} = {\alpha _1}{P_1}{T^2} + {\alpha _2}{P_2}{T^2} + {\alpha _3}{P_3}{T^2} + ... + {\alpha _n}{P_n}{T^2} - \left( {\sum\limits_{i,j} {{\alpha _i}{\alpha _j}{P_i}{P_j}^2} } \right)\]
如果又设\[T = {\beta _1}{P_1} + {\beta _2}{P_2} + {\beta _3}{P_3} + ... + {\beta _n}{P_n}\left( {\sum\limits_{i = 1}^n {{\beta _i} = 1} } \right)\]
那么$QT$距离的平方还有另一种表示式：
\[Q{T^2} =  - \sum\limits_{i,j} {\left( {{\alpha _i} - {\beta _i}} \right)\left( {{\alpha _j} - {\beta _j}} \right){{\left( {{P_i}{P_j}} \right)}^2}} \]

数学星空

现在最后的问题是如何简化本主题的结论，楼上的方法可以得到很长的表达式：

我猜测最终结论为：

\(\sqrt{s}=\sqrt{S}\cos(\frac{\alpha+\beta+\gamma}{3})+\frac{(2k_1-1)a^2\sin(\alpha)+(2k_2-1)b^2\sin(\beta)+(2k_3-1)c^2\sin(\gamma)}{4\sqrt{S}}\)

有谁能给出最简表达式？

creasson

事实上，简化也是容易的，我们来看这两式\[\left\{ \begin{array}{l}
\alpha {\rm{ + }}\beta {\rm{ + }}\gamma {\rm{ = }}1 \\
{\gamma ^2}E{C^2} \times {\sin ^2}C = \left( {\alpha C{D^2} + \gamma D{E^2} - \alpha \beta C{D^2} - \beta \gamma D{E^2} - \gamma \alpha E{C^2}} \right){\sin ^2}\theta  \\
\end{array} \right.\]
将1式代入2式替换掉$\beta$,得到\[\alpha \left( {\alpha  + \gamma } \right)C{D^2} + \gamma \left( {\alpha  + \gamma } \right)D{E^2} = \gamma \left( {\alpha  + \frac{{\gamma {{\sin }^2}C}}{{{{\sin }^2}\theta }}} \right)E{C^2}\]
再令$\gamma：  = \alpha t $,得到单参数方程\[\left( {1 + t} \right)C{D^2} + t\left( {1 + t} \right)D{E^2} = t\left( {1 + \frac{{t{{\sin }^2}C}}{{{{\sin }^2}\theta }}} \right)E{C^2}\]
余下略

creasson

虽然并未做余下的计算，但此时已经可以肯定，最终答案可以表示为一些二次根的简单加减

数学星空

对于\(a=b=c=x\)我们可以得到稍简单一些的结论：

\(x^4(12k_1^2m^2n^2p^2+24k_1k_2m^2n^2p^2+24k_1k_3m^2n^2p^2+12k_2^2m^2n^2p^2+24k_2k_3m^2n^2p^2+12k_3^2m^2n^2p^2-36k_1m^2n^2p^2-36k_2m^2n^2p^2-36k_3m^2n^2p^2-4k_1^2m^2n^2+32k_1^2m^2np-4k_1^2m^2p^2+8k_1k_2m^2n^2+16k_1k_2m^2np+16k_1k_2mn^2p+8k_1k_2mnp^2+16k_1k_3m^2np+8k_1k_3m^2p^2+8k_1k_3mn^2p+16k_1k_3mnp^2-4k_2^2m^2n^2+32k_2^2mn^2p-4k_2^2n^2p^2+8k_2k_3m^2np+16k_2k_3mn^2p+16k_2k_3mnp^2+8k_2k_3n^2p^2-4k_3^2m^2p^2+32k_3^2mnp^2-4k_3^2n^2p^2+27m^2n^2p^2-4k_1m^2n^2-48k_1m^2np+4k_1m^2p^2-16k_1mn^2p-8k_1mnp^2+4k_2m^2n^2-8k_2m^2np-48k_2mn^2p-16k_2mnp^2-4k_2n^2p^2-16k_3m^2np-4k_3m^2p^2-8k_3mn^2p-48k_3mnp^2+4k_3n^2p^2+12k_1^2m^2+24k_1k_2mn+24k_1k_3mp+12k_2^2n^2+24k_2k_3np+12k_3^2p^2-m^2n^2+16m^2np-m^2p^2+16mn^2p+16mnp^2-n^2p^2-12k_1m^2-24k_1mn-12k_2n^2-24k_2np-24k_3mp-12k_3p^2+3m^2+3n^2+3p^2-9)^2+16x^2(36k_1^2m^4n^4p^3-36k_1^2m^4n^3p^4-36k_1k_2m^4n^3p^4+36k_1k_2m^3n^4p^4+36k_1k_3m^4n^4p^3-36k_1k_3m^3n^4p^4-36k_2^2m^4n^4p^3+36k_2^2m^3n^4p^4-36k_2k_3m^4n^4p^3+36k_2k_3m^4n^3p^4+36k_3^2m^4n^3p^4-36k_3^2m^3n^4p^4-36k_1m^4n^4p^3+72k_1m^4n^3p^4+18k_1m^3n^4p^4+72k_2m^4n^4p^3+18k_2m^4n^3p^4-36k_2m^3n^4p^4+18k_3m^4n^4p^3-36k_3m^4n^3p^4+72k_3m^3n^4p^4-12k_1^2m^4n^4p+120k_1^2m^4n^3p^2-120k_1^2m^4n^2p^3+12k_1^2m^4np^4+24k_1^2m^3n^4p^2-24k_1^2m^3n^2p^4+12k_1^2m^2n^4p^3-12k_1^2m^2n^3p^4+24k_1k_2m^4n^3p^2-96k_1k_2m^4n^2p^3+12k_1k_2m^4np^4-24k_1k_2m^3n^4p^2-12k_1k_2m^3n^2p^4+96k_1k_2m^2n^4p^3+12k_1k_2m^2n^3p^4-12k_1k_2mn^4p^4-12k_1k_3m^4n^4p+96k_1k_3m^4n^3p^2-24k_1k_3m^4n^2p^3+12k_1k_3m^3n^4p^2+24k_1k_3m^3n^2p^4-12k_1k_3m^2n^4p^3-96k_1k_3m^2n^3p^4+12k_1k_3mn^4p^4+12k_2^2m^4n^4p-24k_2^2m^4n^3p^2-12k_2^2m^4n^2p^3-120k_2^2m^3n^4p^2+12k_2^2m^3n^2p^4+120k_2^2m^2n^4p^3+24k_2^2m^2n^3p^4-12k_2^2mn^4p^4+12k_2k_3m^4n^4p-12k_2k_3m^4n^3p^2+12k_2k_3m^4n^2p^3-12k_2k_3m^4np^4-96k_2k_3m^3n^4p^2+96k_2k_3m^3n^2p^4+24k_2k_3m^2n^4p^3-24k_2k_3m^2n^3p^4+12k_3^2m^4n^3p^2+24k_3^2m^4n^2p^3-12k_3^2m^4np^4-12k_3^2m^3n^4p^2+120k_3^2m^3n^2p^4-24k_3^2m^2n^4p^3-120k_3^2m^2n^3p^4+12k_3^2mn^4p^4-27m^4n^4p^3-27m^4n^3p^4-27m^3n^4p^4+12k_1m^4n^4p-144k_1m^4n^3p^2+216k_1m^4n^2p^3-24k_1m^4np^4+144k_1m^3n^3p^3+36k_1m^3n^2p^4-36k_1m^2n^4p^3+72k_1m^2n^3p^4-6k_1mn^4p^4-24k_2m^4n^4p+36k_2m^4n^3p^2+72k_2m^4n^2p^3-6k_2m^4np^4+216k_2m^3n^4p^2+144k_2m^3n^3p^3-36k_2m^3n^2p^4-144k_2m^2n^4p^3+12k_2mn^4p^4-6k_3m^4n^4p-36k_3m^4n^3p^2+12k_3m^4np^4+72k_3m^3n^4p^2+144k_3m^3n^3p^3-144k_3m^3n^2p^4+36k_3m^2n^4p^3+216k_3m^2n^3p^4-24k_3mn^4p^4-4k_1^2m^4n^3+72k_1^2m^4n^2p-72k_1^2m^4np^2+4k_1^2m^4p^3-8k_1^2m^3n^4+64k_1^2m^3n^3p-64k_1^2m^3np^3+8k_1^2m^3p^4-4k_1^2m^2n^4p+72k_1^2m^2n^3p^2-72k_1^2m^2n^2p^3+4k_1^2m^2np^4-4k_1k_2m^4n^3+32k_1k_2m^4n^2p-40k_1k_2m^4np^2+4k_1k_2m^3n^4-216k_1k_2m^3n^2p^2+32k_1k_2m^3np^3-32k_1k_2m^2n^4p+216k_1k_2m^2n^3p^2-4k_1k_2m^2np^4+40k_1k_2mn^4p^2-32k_1k_2mn^3p^3+4k_1k_2mn^2p^4+40k_1k_3m^4n^2p-32k_1k_3m^4np^2+4k_1k_3m^4p^3-32k_1k_3m^3n^3p+216k_1k_3m^3n^2p^2-4k_1k_3m^3p^4+4k_1k_3m^2n^4p-216k_1k_3m^2n^2p^3+32k_1k_3m^2np^4-4k_1k_3mn^4p^2+32k_1k_3mn^3p^3-40k_1k_3mn^2p^4+8k_2^2m^4n^3+4k_2^2m^4n^2p+4k_2^2m^3n^4-64k_2^2m^3n^3p-72k_2^2m^3n^2p^2-72k_2^2m^2n^4p+72k_2^2m^2n^2p^3+72k_2^2mn^4p^2+64k_2^2mn^3p^3-4k_2^2mn^2p^4-4k_2^2n^4p^3-8k_2^2n^3p^4-4k_2k_3m^4n^2p+4k_2k_3m^4np^2+32k_2k_3m^3n^3p-32k_2k_3m^3np^3-40k_2k_3m^2n^4p-216k_2k_3m^2n^3p^2+216k_2k_3m^2n^2p^3+40k_2k_3m^2np^4+32k_2k_3mn^4p^2-32k_2k_3mn^2p^4-4k_2k_3n^4p^3+4k_2k_3n^3p^4-4k_3^2m^4np^2-8k_3^2m^4p^3+72k_3^2m^3n^2p^2+64k_3^2m^3np^3-4k_3^2m^3p^4-72k_3^2m^2n^3p^2+72k_3^2m^2np^4+4k_3^2mn^4p^2-64k_3^2mn^3p^3-72k_3^2mn^2p^4+8k_3^2n^4p^3+4k_3^2n^3p^4+9m^4n^4p+18m^4n^3p^2-90m^4n^2p^3+9m^4np^4-90m^3n^4p^2-216m^3n^3p^3+18m^3n^2p^4+18m^2n^4p^3-90m^2n^3p^4+9mn^4p^4+8k_1m^4n^3-104k_1m^4n^2p+112k_1m^4np^2-4k_1m^4p^3-2k_1m^3n^4-16k_1m^3n^3p+240k_1m^3n^2p^2+80k_1m^3np^3-14k_1m^3p^4+12k_1m^2n^4p-48k_1m^2n^3p^2+312k_1m^2n^2p^3-24k_1m^2np^4-16k_1mn^4p^2-16k_1mn^3p^3+20k_1mn^2p^4-14k_2m^4n^3-24k_2m^4n^2p+20k_2m^4np^2-4k_2m^3n^4+80k_2m^3n^3p+312k_2m^3n^2p^2-16k_2m^3np^3+112k_2m^2n^4p+240k_2m^2n^3p^2-48k_2m^2n^2p^3-16k_2m^2np^4-104k_2mn^4p^2-16k_2mn^3p^3+12k_2mn^2p^4+8k_2n^4p^3-2k_2n^3p^4-16k_3m^4n^2p+12k_3m^4np^2-2k_3m^4p^3-16k_3m^3n^3p-48k_3m^3n^2p^2-16k_3m^3np^3+8k_3m^3p^4+20k_3m^2n^4p+312k_3m^2n^3p^2+240k_3m^2n^2p^3-104k_3m^2np^4-24k_3mn^4p^2+80k_3mn^3p^3+112k_3mn^2p^4-14k_3n^4p^3-4k_3n^3p^4+12k_1^2m^4n-12k_1^2m^4p+24k_1^2m^3n^2-24k_1^2m^3p^2-12k_1^2m^2n^3+120k_1^2m^2n^2p-120k_1^2m^2np^2+12k_1^2m^2p^3+12k_1k_2m^4n-12k_1k_2m^3n^2-96k_1k_2m^3np+12k_1k_2m^2n^3+24k_1k_2m^2np^2-12k_1k_2mn^4+96k_1k_2mn^3p-24k_1k_2mn^2p^2-12k_1k_3m^4p+96k_1k_3m^3np+12k_1k_3m^3p^2-24k_1k_3m^2n^2p-12k_1k_3m^2p^3+24k_1k_3mn^2p^2-96k_1k_3mnp^3+12k_1k_3mp^4+12k_2^2m^3n^2-24k_2^2m^2n^3-120k_2^2m^2n^2p-12k_2^2mn^4+120k_2^2mn^2p^2+12k_2^2n^4p+24k_2^2n^3p^2-12k_2^2n^2p^3+24k_2k_3m^2n^2p-24k_2k_3m^2np^2-96k_2k_3mn^3p+96k_2k_3mnp^3+12k_2k_3n^4p-12k_2k_3n^3p^2+12k_2k_3n^2p^3-12k_2k_3np^4-12k_3^2m^3p^2+120k_3^2m^2np^2+24k_3^2m^2p^3-120k_3^2mn^2p^2+12k_3^2mp^4+12k_3^2n^3p^2-24k_3^2n^2p^3-12k_3^2np^4+5m^4n^3+38m^4n^2p-38m^4np^2+m^4p^3+m^3n^4-24m^3n^3p-252m^3n^2p^2-24m^3np^3+5m^3p^4-38m^2n^4p-252m^2n^3p^2-252m^2n^2p^3+38m^2np^4+38mn^4p^2-24mn^3p^3-38mn^2p^4+5n^4p^3+n^3p^4-24k_1m^4n+12k_1m^4p+12k_1m^3n^2+48k_1m^3np+48k_1m^3p^2-24k_1m^2n^3+120k_1m^2n^2p+336k_1m^2np^2-36k_1m^2p^3+6k_1mn^4-48k_1mn^3p+48k_1mn^2p^2+48k_1mnp^3-6k_1mp^4-6k_2m^4n-36k_2m^3n^2+48k_2m^3np+48k_2m^2n^3+336k_2m^2n^2p+48k_2m^2np^2+12k_2mn^4+48k_2mn^3p+120k_2mn^2p^2-48k_2mnp^3-24k_2n^4p+12k_2n^3p^2-24k_2n^2p^3+6k_2np^4+6k_3m^4p-48k_3m^3np-24k_3m^3p^2+48k_3m^2n^2p+120k_3m^2np^2+12k_3m^2p^3+48k_3mn^3p+336k_3mn^2p^2+48k_3mnp^3-24k_3mp^4-6k_3n^4p-36k_3n^3p^2+48k_3n^2p^3+12k_3np^4+36k_1^2m^2n-36k_1^2m^2p-36k_1k_2m^2n+36k_1k_2mn^2+36k_1k_3m^2p-36k_1k_3mp^2-36k_2^2mn^2+36k_2^2n^2p-36k_2k_3n^2p+36k_2k_3np^2+36k_3^2mp^2-36k_3^2np^2+9m^4n-3m^4p+18m^3n^2-24m^3np-18m^3p^2-18m^2n^3-252m^2n^2p-252m^2np^2+18m^2p^3-3mn^4-24mn^3p-252mn^2p^2-24mnp^3+9mp^4+9n^4p+18n^3p^2-18n^2p^3-3np^4-18k_1m^3+72k_1m^2n+108k_1m^2p-36k_1mn^2+144k_1mnp+108k_2mn^2+144k_2mnp-18k_2n^3+72k_2n^2p-36k_2np^2-36k_3m^2p+144k_3mnp+72k_3mp^2+108k_3np^2-18k_3p^3+9m^3-18m^2n-54m^2p-54mn^2-216mnp-18mp^2+9n^3-18n^2p-54np^2+9p^3+54k_1m+54k_2n+54k_3p-27m-27n-27p)s-(16(3n^2p^2-n^2+8np-p^2+3))(3m^2p^2-m^2+8mp-p^2+3)(3m^2n^2-m^2+8mn-n^2+3)s^2=0\)

进一步当\(k_1=k_2=k_3=k\)时：

\(x^4(108k^2m^2n^2p^2-108km^2n^2p^2+72k^2m^2np+72k^2mn^2p+72k^2mnp^2+27m^2n^2p^2-72km^2np-72kmn^2p-72kmnp^2+12k^2m^2+24k^2mn+24k^2mp+12k^2n^2+24k^2np+12k^2p^2-m^2n^2+16m^2np-m^2p^2+16mn^2p+16mnp^2-n^2p^2-12km^2-24kmn-24kmp-12kn^2-24knp-12kp^2+3m^2+3n^2+3p^2-9)^2+16x^2(54km^4n^4p^3+54km^4n^3p^4+54km^3n^4p^4+216k^2m^4n^3p^2-216k^2m^4n^2p^3-216k^2m^3n^4p^2+216k^2m^3n^2p^4+216k^2m^2n^4p^3-216k^2m^2n^3p^4-27m^4n^4p^3-27m^4n^3p^4-27m^3n^4p^4-18km^4n^4p-144km^4n^3p^2+288km^4n^2p^3-18km^4np^4+288km^3n^4p^2+432km^3n^3p^3-144km^3n^2p^4-144km^2n^4p^3+288km^2n^3p^4-18kmn^4p^4+144k^2m^4n^2p-144k^2m^4np^2-144k^2m^2n^4p+144k^2m^2np^4+144k^2mn^4p^2-144k^2mn^2p^4+9m^4n^4p+18m^4n^3p^2-90m^4n^2p^3+9m^4np^4-90m^3n^4p^2-216m^3n^3p^3+18m^3n^2p^4+18m^2n^4p^3-90m^2n^3p^4+9mn^4p^4-6km^4n^3-144km^4n^2p+144km^4np^2-6km^4p^3-6km^3n^4+48km^3n^3p+504km^3n^2p^2+48km^3np^3-6km^3p^4+144km^2n^4p+504km^2n^3p^2+504km^2n^2p^3-144km^2np^4-144kmn^4p^2+48kmn^3p^3+144kmn^2p^4-6kn^4p^3-6kn^3p^4+24k^2m^4n-24k^2m^4p+24k^2m^3n^2-24k^2m^3p^2-24k^2m^2n^3+24k^2m^2p^3-24k^2mn^4+24k^2mp^4+24k^2n^4p+24k^2n^3p^2-24k^2n^2p^3-24k^2np^4+5m^4n^3+38m^4n^2p-38m^4np^2+m^4p^3+m^3n^4-24m^3n^3p-252m^3n^2p^2-24m^3np^3+5m^3p^4-38m^2n^4p-252m^2n^3p^2-252m^2n^2p^3+38m^2np^4+38mn^4p^2-24mn^3p^3-38mn^2p^4+5n^4p^3+n^3p^4-30km^4n+18km^4p-24km^3n^2+48km^3np+24km^3p^2+24km^2n^3+504km^2n^2p+504km^2np^2-24km^2p^3+18kmn^4+48kmn^3p+504kmn^2p^2+48kmnp^3-30kmp^4-30kn^4p-24kn^3p^2+24kn^2p^3+18knp^4+9m^4n-3m^4p+18m^3n^2-24m^3np-18m^3p^2-18m^2n^3-252m^2n^2p-252m^2np^2+18m^2p^3-3mn^4-24mn^3p-252mn^2p^2-24mnp^3+9mp^4+9n^4p+18n^3p^2-18n^2p^3-3np^4-18km^3+72km^2n+72km^2p+72kmn^2+432kmnp+72kmp^2-18kn^3+72kn^2p+72knp^2-18kp^3+9m^3-18m^2n-54m^2p-54mn^2-216mnp-18mp^2+9n^3-18n^2p-54np^2+9p^3+54km+54kn+54kp-27m-27n-27p)s-(16(3n^2p^2-n^2+8np-p^2+3))(3m^2p^2-m^2+8mp-p^2+3)(3m^2n^2-m^2+8mn-n^2+3)s^2=0\)

再进一步当\(k=\frac{1}{2}\)时

\(x^4(-m^2n^2-2m^2np-m^2p^2-2mn^2p-2mnp^2-n^2p^2-6mn-6mp-6np-9)^2+16x^2(2m^4n^3+2m^4n^2p-2m^4np^2-2m^4p^3-2m^3n^4+2m^3p^4-2m^2n^4p+2m^2np^4+2mn^4p^2-2mn^2p^4+2n^4p^3-2n^3p^4+12m^3n^2-12m^3p^2-12m^2n^3+12m^2p^3+12n^3p^2-12n^2p^3+18m^2n-18m^2p-18mn^2+18mp^2+18n^2p-18np^2)s-(16(3n^2p^2-n^2+8np-p^2+3))(3m^2p^2-m^2+8mp-p^2+3)(3m^2n^2-m^2+8mn-n^2+3)s^2=0\)

看来对于一般情形找到最简表达式并非易事！